數控凸輪軸磨床運動（dòng）誤差分析（xī）與建模技術（shù）-數控機床市場網

您現在的位（wèi）置：磨床（chuáng）網> 技術前沿>數控凸（tū）輪軸磨床運動誤差分析與建模（mó）技術

數（shù）控凸輪軸（zhóu）磨床運（yùn）動誤差分析與建模技術

2018-8-7 來源：北京工業大學機械工程與應用電子技術（shù）學院作（zuò）者：範晉偉，王鴻亮，張蘭清，唐宇航

摘要: 為了對某數控凸輪軸磨（mó）床的運動（dòng）誤差進（jìn）行分析（xī）和建模，分析（xī）研（yán）究了各運動部件間運動形式和誤差類型，運（yùn）用相鄰體坐標係間的運動變化來表達 2 相鄰體之間的運動情況，建立了（le）相鄰體之間的理想運動方程和有誤差情況下的實際運動方（fāng）程．將相鄰體（tǐ）間的實際運動（dòng）方程（chéng）進一步推廣到任意低序體陣列分析當中，為研究多分支數控凸輪（lún）軸磨床誤差建模提供理論（lùn）基礎．將複雜的多分支鏈數控凸輪軸（zhóu）磨床抽象（xiàng）為簡單的多（duō）體係統，對各運動部件（jiàn）建立相應的體坐（zuò）標係和（hé）運動參考坐標係，求出相鄰體間對應的變（biàn）換矩陣．最後，將機床運動部件劃分為“工件－床身”和“砂輪－床身”2 條運動（dòng）鏈（liàn），提出了有誤差影響（xiǎng）情況下實現精密加工約束（shù）條件方程為 Pw= Pt，且對該方（fāng）程進行了求解，為（wéi）數（shù）控凸輪軸磨床（chuáng）誤差補償（cháng）的研（yán）究提供（gòng）了必要條件．結果（guǒ）表明: 誤差補償後的機床加工精度顯著提高．

關鍵詞: 數控凸輪軸磨床; 誤差分析; 多體係（xì）統; 運動關係; 誤差（chà）建模

凸（tū）輪（lún）軸廣泛用（yòng）於汽車、摩（mó）托車、內燃機等發動機，主要控（kòng）製氣門的開啟與閉合，其輪廓的加工精度直接（jiē）影響發（fā）動（dòng）機的（de）工作性能．數控凸（tū）輪軸磨床作為最常用的高效（xiào）、高（gāo）精度凸輪軸加工最後一道工序設備，其精度保持性至（zhì）關重要．但（dàn）考慮到所有機（jī）床均會麵（miàn）臨工作中由於各種誤差（chà）引起的工作精度降低問題，這就需要對機床進行誤差（chà）分（fèn）析，並采（cǎi）取適當措施進（jìn）行誤差防止或誤差補償．因此，減小誤差對機床加工精度（dù）的影響方（fāng）法可分為誤差防止法和誤差補償（cháng）法．誤差補償法（fǎ）是在不改變原有機床的基礎上，通過建立機（jī）床誤差模型，辨識機床各項誤差並（bìng）通過修正數控（kòng）指令的方法來減小機床誤差對工件加工精度的影響．誤差補償法克服了（le）傳統誤差防（fáng）止法費用高、適用性差等缺（quē）點而得到了迅速發展．機床（chuáng）運動誤差分析與建模是（shì）誤差補償的（de）基礎，對機床誤差能否正（zhèng）確分析是（shì）誤差（chà）建模的關鍵問題．為提高數控凸輪軸磨床加工精度以及精（jīng）度保持性，有必要對（duì）數控凸輪軸磨床的運動誤差分析與建模進行研究．目前，國內（nèi）外對數控機床誤差補償技術的研究主要（yào）有: 粟時平采用（yòng）多體係統理論對多軸數控機床精度建模與誤差補償方法進（jìn）行了研（yán）究．範晉偉等對提（tí）高精密凸輪磨削精度的幾何誤差補償技術進行了研究．李建對凸（tū）輪軸數控磨削誤差分析和補償技（jì）術進行（háng）了研究和軟件設計．王維等采用（yòng）多項式擬合與線性（xìng）擬合方法（fǎ）對數控機床幾何（hé）誤差與熱誤差進行綜合建模和誤差在線實時補（bǔ）償．王曉峰對複合數控機床幾何誤差（chà）補償（cháng）及誤差影響溯源進行了分析． Lechniak 等提出了利用離線軟件進行誤差（chà）補償． Chnan 等對三軸磨床幾何和力的誤差補償進行了研究． ZHANG 等利用雙球杆（gǎn）儀對（duì）五軸數控機（jī）床回轉（zhuǎn）工作台誤差進行了檢（jiǎn）測和補償．

機床一（yī）般都（dōu）是由多個運動體組成的複雜機械係統，多體係統理論是將（jiāng）對複雜機（jī）械（xiè）係統的分析分解為對運動體分析，然後將其耦合．數控凸輪軸磨床是特殊輪廓加工（gōng）機床，隨著近年來（lái）隨動（dòng）式凸輪（lún）軸（zhóu）磨床的應用（yòng）越來越廣泛，以（yǐ）往的誤差分析和建模（mó）方法太過於複（fù）雜，機床誤差建模又缺乏通用（yòng）模型，不同類型的（de）機床需建立不同的（de）誤差模型，而多體係統理論能用於降低機床誤差建模的難度，很少有人將多體係統理論應用到該機床誤差建（jiàn）模中，因此本文采用多體係統理論對隨動（dòng）式（shì）數控凸輪（lún）軸磨床進行了（le）建模技術研究.

1、數控（kòng）凸輪軸（zhóu）磨床運動（dòng）分析及誤差分類

對某隨動式數控凸輪軸磨床進行三維建模並簡化，其結構示意圖如（rú）圖 1 所（suǒ）示．該機床是一種特殊的三軸機床，其運動包括砂輪架沿砂輪架底座的 x向移動，工作台沿（yán）床身的 z 向移動以及主軸帶（dài）動工件（jiàn）繞 c 軸（zhóu）的轉動．在（zài）工作中主要是通過（guò）控製 x 軸和c 軸的聯動（dòng）來完成凸輪輪廓的加工．通過多個運動單元組成的（de）機（jī）床，各運動單元的誤差可（kě）分為與（yǔ）位置點無關的誤（wù）差和與位置點有關的誤差．與位（wèi）置點無關的（de）誤（wù）差包括: x 軸與 z 軸（zhóu）和 c 軸之間的垂直度誤差以（yǐ）及 z 軸與 c 軸之間的平行度誤差，如圖 2( a) 所（suǒ）示．在空間坐標係中任意物體均有 6 個自（zì）由度，在運動過（guò）程中必然產出 6 項誤差，3 項線位移誤差和 3 項角位（wèi）移誤差，這些誤差是與位置點有關（guān）的誤差，三軸機床共有 18 項與位置點有關的誤差，以 x 向移動部件為例來（lái）說明（míng）如圖 2( b) 所示，各項運動誤差參數如表 1 所示．

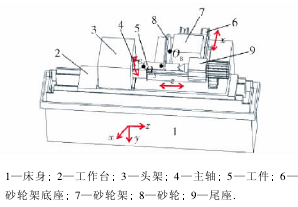
圖 1 數控凸輪軸磨（mó）床結構

表 1 數控凸（tū）輪軸磨床幾何誤差參數

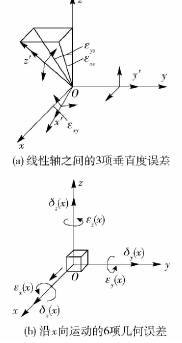
圖 2 誤差（chà）參數

2 、數控凸輪軸磨床拓撲結構及低序體陣列描述

多體係統是指由多個剛體或柔性（xìng）體通過（guò）某種形（xíng）式連接而成的複雜機械係統（tǒng），多體係統運動學理論是指將機床的各個運動部件看作不同的剛體，對每個剛體分別建立體（tǐ）坐標係和運動坐標係，並（bìng）對多體係統每個分支按照由小到大的順序進行排列，將機床的運動變（biàn）為剛體坐標係之間的運（yùn）動，對機床的運動分析變為多體坐標係之間的（de）運動分析．利用多體係統運動學理論對該數控機床進行拓撲結構及低序體陣列描述，以（yǐ）床身為分支起點（diǎn），按床身－砂輪和床身－工（gōng）件分支劃分，最後再以磨削點位置為終點，使機床組成閉環係統．故該機（jī）床共有 2 條運動（dòng）鏈，分別是（shì）由（yóu） 1-6-7-8 體組成的床身－砂（shā）輪鏈（liàn）( B-T) 和 1-2-3-4-5 體組成的床身－工件鏈( B-W) ．該機床的拓撲結（jié）構圖如圖 3 所示．拓撲結構的低序體陣列（liè）如表2 所示（shì）．

3 、相鄰體運（yùn）動關係模型的建（jiàn）立

對機床各運動部件進行分解，研究（jiū）相鄰（lín）體間的運（yùn）動學關係，最後通過（guò）變換矩陣乘積耦合建立整個機床的（de）運動模型（xíng），可（kě）以大大降低直接研究多個運（yùn）動體關係的複雜度.

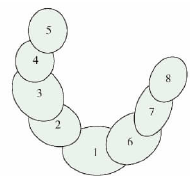
圖（tú） 3 數控凸輪軸磨床拓撲結構（gòu）

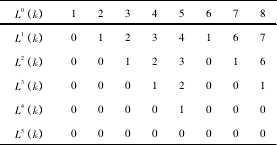
表（biǎo） 2 數控凸輪軸磨床拓撲（pū）結構的低（dī）序體陣列

3. 1 理想情況下相鄰體運動關係模型的建立

圖 4 為（wéi）理想情況（kuàng）下相鄰體（tǐ） Bi和 Bj的相互關（guān）係，Oi和 Oj分別為兩相鄰體的體坐標係，Qj為（wéi）固定在 Bi體上的 Bj的運動參考點，Bj相對於 Bi的相（xiàng）對位置可用 Qj相對於 Oi的位置矢（shǐ）量 pj來（lái）表示，Bj相（xiàng）對於 Bi的（de）相對移動（dòng）可用 Oj相對於 Qj的位移矢量 sj來表示，Ｒ為慣性坐（zuò）標係，因此相鄰體間的（de）運動關係可由相鄰體坐（zuò）標係之間的變化來表示．

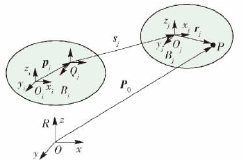
圖（tú） 4 理想情況下相鄰（lín）體相對運動

設 P 為 Bj體上任意一點，由上述分析可知，P在 Oi-xiyizi坐（zuò）標係中的位置矢量為.

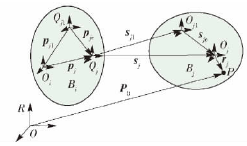
圖（tú） 5 有誤差（chà）情況下（xià）相鄰體相對運動示意圖

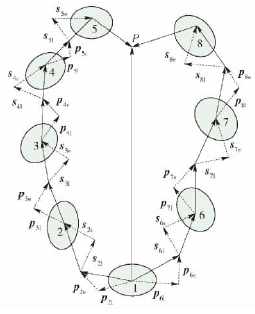
圖 6 數控凸輪軸磨床拓撲（pū）結構

為實現機（jī）床（chuáng）精密加工，必須使砂輪磨削點在（zài）慣性坐標係中的坐標與工件磨削點在慣性（xìng）坐標係中的

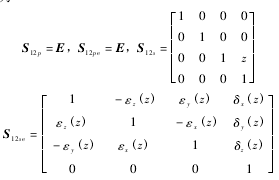
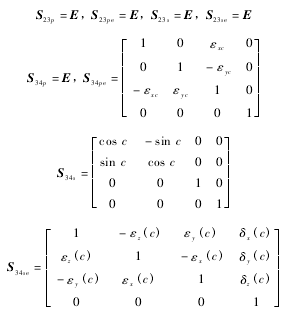
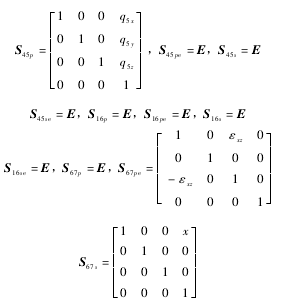
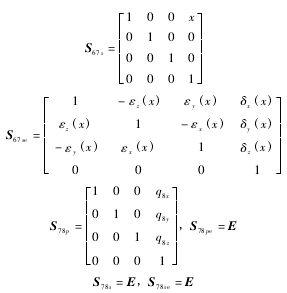
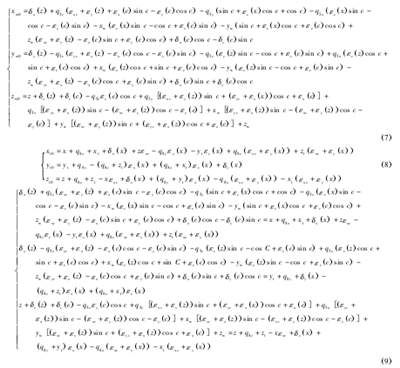
精密加工約束方程中的 21 項（xiàng）誤差參（cān）數可通（tōng）過雙球（qiú）杆儀並配合多（duō）體係統理論進（jìn）行（háng）測量和（hé）辨識，通過建立刀具路線和數控指令的映（yìng）射關係以及（jí）數控指令和實際刀具軌跡的映射關係（xì），利用這 2 個關係可以對有誤差情況（kuàng）下的數控指令進行修正，並進行判別得（dé）到滿（mǎn）足精度要求的數控指令值，考慮到篇幅（fú）問題對於誤差補償過（guò）程不在敘述．該方法已進行了實驗，利用誤補償後的機床（chuáng）加工某（mǒu）汽車發動機進排氣凸輪軸，通（tōng）過與補償前機床加工比較凸輪軸的最大升程誤差已由（yóu） 22 μm 降到了 9 μm，由此可見，誤差補償後的機床加工精度已顯著提高．

5 、結論

1) 對數控凸輪（lún）軸（zhóu）磨床基本結構進行了（le）分析，各相鄰體之間的連接形式分別為剛性連接、導軌滑動（dòng）連接和軸承（chéng）連接的（de）一種特殊的多體係統．因此可將數控（kòng）凸輪軸磨床直接抽象為具有“工（gōng）件－床身”和“砂輪－床身”2 條運動（dòng）鏈的開環多體係統，完全（quán）可以利用多體係統運動學理論對機床進（jìn）行簡化分析和（hé）建模，最後再以工件磨削（xuē）點和砂輪磨削點重合使係統形成閉環係統．

2) 對數（shù）控凸輪軸（zhóu）磨床（chuáng）幾何誤（wù）差進行了分析，將誤差類型分為了與位置點無關誤差和與（yǔ）位置點（diǎn）有關誤差，分析了不同類型（xíng）誤差的作用機理，提出了誤（wù）差參（cān）數的描（miáo）述（shù）方法．

3) 運用多體係統誤差分析理論，對數控凸輪軸磨床建立了誤差分析模型，推導出了工件磨削點運動約束方程的表（biǎo）達式，給出了實現精密加工的必要條件，為數（shù）控凸輪軸磨床誤差（chà）補償的研究提（tí）供了必要條件．

投稿箱：
如果您有機床行業、企業相關新（xīn）聞稿件發表，或進行（háng）資訊（xùn）合作，歡迎聯係（xì）本網編輯部，郵箱：skjcsc@vip.sina.com

更多相（xiàng）關信息

名企推薦

業界視點（diǎn）

| 更多

行業數據

| 更多

博文選萃

| 更多

數（shù）控機床