基（jī）於目標規劃的履帶可變形機器人結構參數設計及驗（yàn）證-機（jī）器人-數控機床市（shì）場網（wǎng）

您現在（zài）的（de）位置：機器人> 技術前沿>基（jī）於目標規劃的履帶可變形機（jī）器人結構參數設計及驗證

基於目（mù）標規劃的履帶可變形機器（qì）人結構參（cān）數設計及驗證

2016-9-13 來源：中國科學院沈陽自動化研究所機器人等作者：朱岩王明輝李斌王聰（cōng）

摘要：機器人結構（gòu）參數直接影響其對環境的（de）適應能力，因此合理的結構參數設計至關重要。為更高效設計能適應障礙已知環（huán）境的機器人，該（gāi）研究提出一種基於目標規劃的機器人結構（gòu）參數設（shè）計方法，以得到能適應該（gāi）環境的結構參數最優的機器人，並開發樣機進行（háng）試驗驗證。首先提出並設計履帶可（kě）變（biàn）形機器人模型，在分析機器人越障機理基礎上，建立（lì）機器人（rén）能夠跨越（yuè）的（de）台階和溝壑障礙與其結（jié）構參數間的關係，並（bìng）在此基礎上建立履帶可變形機器人的結構參數目標規劃模（mó）型。利用遺傳算法得到該目標規劃問題的最優結構參數：履帶輪半徑60 mm，擺臂最大長度326 mm，機（jī）體長度290 mm，並利用Adams 建立仿真模型驗證了機器人對目標環境的適應性。樣機試驗表明機器人能夠跨越160 mm 高台階和300 mm寬溝壑，證明了計（jì）算得到的結構參數的（de）合理性，及基於目標規劃的（de）機（jī）器人結構參數設計方法的可行（háng）性。該研究可為機器人的結構（gòu）參數設計提供參考。

關鍵詞：機器人；遺傳算（suàn）法；優化；目標規劃；履帶可變形機器人；結構參數

0、引言

近（jìn）些年來，機器人已經廣泛應用於（yú）救援、檢修、農業和軍事等（děng）場合代替人（rén）類執行（háng）任務。其（qí）中，履帶式（shì）移動機器人因其（qí）較好的環境適應性和較簡單的結構（gòu）形式，得到了廣泛的（de）研（yán）究和應用（yòng）。目前，已知履帶機器人有Packbot[1]和“靈犀”機器（qì）人[2]等履帶不可變形機器人，VCTV-1（variable configuration tracked vehicle-1）機器人（rén）[3]，VGTV-2 機器人[4]，VCTV-3 機器人[5]，VGST 機器（qì）人[6-8]，法（fǎ）國VGTV 機器人[9]，NEZA-I 機器人[10]和履帶自張緊（jǐn）式主臂可變構型機器人[11]等履（lǚ）帶可（kě）變（biàn）形機器人。然而多數機器人均針對非結構環境（jìng）設計，由於（yú）非結（jié）構環境的複雜性，致使設（shè）計得到的機器人較為（wéi）笨重，應用於核潛艇、室內以及特定農作物種植區等障礙已知的結構環境很不經濟。然而（ér），這樣的環境對於機器人的需求越來越多，尤其是隨著農業對於機器人的（de）需求量日益增大（dà）。在農業（yè）應用中，農作物行間距以及灌溉溝渠等都是已知障礙（ài），屬於典型的結構環境。機器人機構設計直（zhí）接影響其對環境的適應（yīng）性，如何設計合理的機器人（rén）本體結構參數成為亟待解決的問題。由於環境（jìng）障礙的多樣性以及對機器人自身（shēn）性能的多種（zhǒng）要求（qiú），例如，在農業應用上，要求機器人能順利通過具有（yǒu）特定行（háng）間（jiān）距的作物並且跨越相應的灌溉溝渠，因（yīn）此，機（jī）器人本體結構參數（shù）的設計問題成為多目標優（yōu）化問題。李楠等[12]使用Pareto 模型處（chù）理多（duō）目標問題對水陸（lù）兩棲可變形機器人的結構參（cān）數進行了分析設計，Sergiu 等 [13]使用分量加權方法處理（lǐ）多目標問題對並聯機（jī）器人進行了設計分析，劉建等[14]提出了基於多目標粒子群優化（huà）算法的礦用救援機器人動力匹配設計方法，Luo Yang[15]采用多目標優化方法設計了輪腿複合機器人Rolling-Wolf。這些（xiē）設計方法在機器人結構設計（jì）研究中均使用性能函數的極值作（zuò）為設計目（mù）標，很難應用於環境障礙已（yǐ）知、對機器人性能提出具體目標要求（qiú）的環境，因（yīn）為采用性能極（jí）值得到的結構參數值不一定能滿足環境（jìng）中最大障（zhàng）礙對機器人的要求，即（jí）對環境（jìng）的（de）適應性得不（bú）到（dào）保障。因此，本文使用目標規劃（goal programming）處理（lǐ）多目標優化問題，將已知環境中（zhōng）障礙最值作為目標賦予性能函數，將性（xìng）能函數與預期目標（biāo）間的偏差作（zuò）為目標函數，以設計（jì）最優的機（jī）器（qì）人結構參數。

本文在分析履帶機器人構（gòu）型演化機理基礎上，以履帶（dài）可（kě）變形機器人作為研究（jiū）對（duì）象（xiàng），將橢圓定理應用於其（qí）構（gòu）型機理設計，進一步在（zài）分（fèn）析機器人越（yuè）障機理基礎上（shàng），建立目標規劃模型，並使（shǐ）用（yòng）遺傳算法得到可行解，以指導選取合理的機器人結構參（cān）數。最（zuì）後，通過仿真和試驗對機器人結構參數的合理性進行驗證。

1、履帶可變形機器人目標（biāo）規劃模型

1.1 機器人機構原理設計（jì）

1.1.1 概（gài）念設計

一般而（ér）言，履帶式移動機器人底盤至少需要2 個驅動，以保證機器人（rén）可以完成轉向運動。而對（duì）於（yú）含有擺臂（bì）的機器人，其驅動數隨（suí）著主動擺臂個數的（de）增加而增加，同時機器人的成本和結構的複雜度也（yě）隨（suí）之（zhī）增加，如圖1a所示，是基本（běn）的履帶機器人構型演化圖，圖（tú）1b 是在假設A 構（gòu）型越障性能和複雜度均為2 的基礎上對各個構型機器人（rén）性（xìng）能估（gū）計值的對比圖。

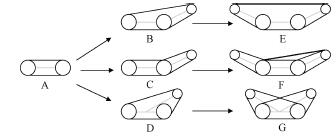
a. A～G 構型（xíng）推演

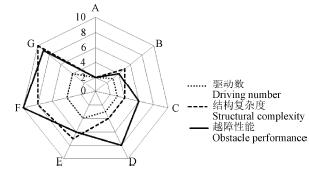
b. 構型（xíng）特性對比

注：對於（yú）驅動數，0～10 表示機器人所需的最少驅動數。對於越障性（xìng）能和結構複（fù）雜度，0～10 表示機器人的越障性（xìng）能和結構複雜度，數值越大，越障性能越強、結構複雜度越大。

圖1 履帶（dài）機器人構型推演與構（gòu）型特（tè）性圖

由圖1 可知，構型D 使用3 個驅動和較簡單的結構形式，實現了單臂（bì）複用，具有很好的環（huán）境適應能力。基於以上考慮，本文對構（gòu）型D 進（jìn）行分（fèn）析研究（jiū），設計合理的結構參數，以適應特定的環境。

1.1.2 構型原理設計

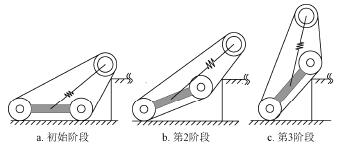
對於履帶可變（biàn）形機器人（rén）構（gòu）型D，設計中要解決的重要問題（tí）是如何保證（zhèng）履帶張緊的同（tóng）時履帶（dài）長度不發生變化（huà）。如（rú）圖2a 所示，可知履帶長度為

式中Lbelt 為履帶的總長度，mm；Lc 為驅動輪O1 和被動輪（lún）O2 中心間距，mm；O1P L 為驅動輪中（zhōng）心O1 點到行星輪中心P 的距離（lí），mm；O2P L 為被動輪中心O2 點到行星輪中心P 的距離，mm；ri(i=1,2,3)分別為驅動輪O1，被（bèi）動輪（lún）O2 和行星輪P 的半徑，mm；θi(i=1,2,3)分別（bié）為履帶在驅動（dòng）輪O1，被動輪O2 和行星輪P 上的包角，rad。

假設O1、O2 分別位（wèi）於橢圓的2 個焦點位置，La 為擺臂（bì）最大長度，mm；Lb 為（wéi）擺臂最小長度，mm；γ 為擺臂OP 與O1O2 連線間的銳角，rad。根據橢圓定（dìng）義，如果（guǒ）保證擺臂實時長度（dù）L 在其旋轉過程中（zhōng）滿足

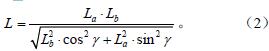
則LO1P + LO2P = 2La 為常數。

由於O1、O2 和P 始終構成（chéng）三角形（xíng），因此，履帶在（zài）帶輪上的包角之和始終（zhōng）為2π。假設3 個帶輪半徑（jìng）相等且（qiě）均為r，則履帶長度僅與機器人的幾何參數有關，為

采用圖2b 所示彈（dàn）簧和凸輪機構來實現擺臂按照式

（2）變化且履帶能連續張緊。

注：La 為擺臂最大長度，mm；Lb 為擺（bǎi）臂最小長度，mm；Lc 為驅動輪和被動（dòng）輪中心間距，mm；γ 為擺臂OP 與O1O2 連線間的銳（ruì）角，rad；ri(i=1,2,3)分別（bié）為驅動輪O1、被動輪（lún）O2 和（hé）行星輪（lún）P 的半（bàn）徑，mm；θi(i=1,2,3) 分別為履帶在驅動輪輪O1，被動輪O2 和行星輪P 上的包（bāo）角，rad。

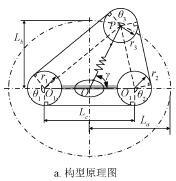
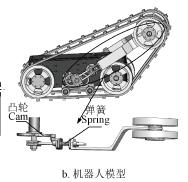
圖2 機器人構型原理及模型

1.2 越障機理分析

為合理規劃機器人結構參數，提（tí）高機器人對目標環境的適應能力，需要構建機器人結構參（cān）數與能夠跨越的障礙（ài）間的（de）關係。本文分（fèn）析機器人在工作（zuò）環境中普遍存在（zài）的台階（jiē）和溝壑2 種（zhǒng）不同類型障礙。

1.2.1 攀爬台階

對於不同大小的台階，機器人將采取不同策略跨越（yuè），當障礙小於驅動輪（lún）半（bàn）徑時（shí），類（lèi）似輪式（shì）機（jī）器人，機器人隻需前進，無需擺臂的額外輔助即可（kě）完成障（zhàng）礙的跨越。當台階比驅動輪半徑稍大（dà）時，可以通過擺臂前擺的方式撐起機體跨越障（zhàng）礙。而（ér）機（jī）器人能夠跨越的最大障礙是當擺臂後擺撐起機體時，如圖3 所示。

對於較（jiào）大台階的跨越，共分為3 個過程（chéng）：

1）擺臂前（qián）擺，支撐起機體，直至（zhì）機體處履帶與台（tái）階接觸，如圖3a～圖3c 所示；

2）擺臂後擺支撐起機體，同時驅動輪驅動機器人前行，直至機器人重心越過台階邊界線，如圖3d～3e 所示；

3）擺臂逐漸（jiàn）恢複到（dào）越障前的狀態（tài），如圖3f 所示。

機器人越障的關鍵（jiàn）狀態如圖3e，此時機器人重心達到台階邊界（jiè）線。假設履帶不彎（wān）曲，x 軸平（píng）行於與障礙接觸處的履帶，則在機器人剛脫離與地麵接觸時應不打滑，滿足

式中Ff 為台階對機器人的（de）摩擦力，N；FN 為台階對機器人的支撐力，N；f 為台階和履帶間的摩擦係數。

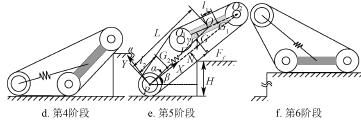
注：X 和（hé）Y 分別為直角（jiǎo）坐標係的2 個（gè）方向，原點位於行星輪中心P 點，X 方向沿（yán）P 點指（zhǐ）向O2 點，Y 垂（chuí）直於X；L 為擺臂實時長度，mm；l1 為機體質心G1 到（dào）機體幾何（hé）中心O 的距離，mm；l2 為擺臂質心G2 到原點P 的距（jù）離，mm；β 為x 軸與水平麵夾角，rad；H 為台階高度（dù），mm；Ff 為台階對機器人的摩擦力，N；FN 為台階對機器人的支撐力，N。

圖3 機器人攀爬台階過（guò）程

此時台階高度與機器人（rén）質心（xīn）滿足

式中H 為台階高度，mm；xG 和yG 分別為機（jī）器人重心X軸和Y 軸（zhóu）的（de）坐標值，mm；β 為x 軸與水（shuǐ）平麵夾角（jiǎo），rad；r 為機（jī）器人驅動輪半徑，mm。

設機（jī）器人機體質量為m1，kg；擺臂質量為m2，kg；擺臂與x 軸夾角為α，rad。如圖3e 所示（shì），機器（qì）人（rén）質心（xīn）坐（zuò）標為

由圖3e 中△OO2P，根（gēn）據正弦定理可知

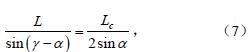
式中α 為擺臂與x 軸夾角（jiǎo），rad。

由式（7）知，γ 確（què）定後，α 也確定。再結合式（6）知，質（zhì）心位置僅與擺臂實時長度L 和轉角γ 有關。又H對質心的偏導數（shù）滿足

因此機器人重心xG 坐標值越大，可以跨越的障礙也越高，顯然增加擺臂長度可以增大xG 坐標值。並且隨著yG 坐標增大，機器人能夠（gòu）跨越的障礙越小，因此應保證yG 足夠小。

又質心（xīn）對擺臂OP 與O1O2 連線間的銳角（jiǎo）γ 的偏導數滿足

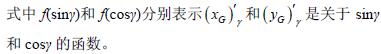
因此擺臂擺動過程中，OP 與O1O2 連線間的銳角γ 越小擺臂越長，此時能夠跨越的障礙也越大。由於γ ∈[0,90°]，可知，當γ=0 時，機器人跨越的障礙最大。

1.2.2 跨越溝壑

對於該擺臂可伸縮式履帶機器人，通過擺臂的（de）前擺和後擺（bǎi）可調節重心位置，可以跨越很大的溝壑障礙。如圖4 所示，機器人跨越較大（dà）溝壑（hè）過程（chéng）可以分為2 個階（jiē）段：

1）擺臂前擺前進直至機器人機體橫跨障礙；

2）擺臂後擺前行直（zhí）至越（yuè）過溝壑。

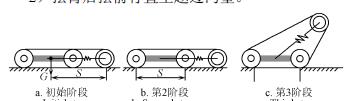
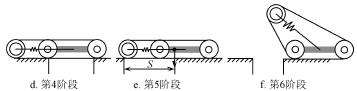
圖4 機器人跨（kuà）越溝壑過程

由圖4 可知，影響機器人跨越（yuè）溝壑（hè）寬度的為圖4a，圖4b 和（hé）圖4e。其中，圖4a 和圖4e 能越（yuè）過的溝壑寬度由機器人重心到（dào）擺臂末端的距離決定，且兩者中較小的距離決定了兩狀態能跨（kuà）越的溝壑的最大值。又因為機體質心與機體幾何中心存在偏置l1，因此，溝壑長度由擺臂轉向質（zhì）心偏置方向時決（jué）定，為

同理，對式（10）求α 的偏導可知

式中f(sinγ)表（biǎo）示(xGS )α′ 是關於sinγ 的函數。

因此，α 值越小機器人在圖4a 和（hé）圖4e 階段跨越（yuè）的溝壑越寬，又由式（7）可知γ 與α 正（zhèng）相關，同攀爬台階類似，可得γ=0 時xGS 有（yǒu）最大值。

對於圖4b，此過程中機器（qì）人應能夠橫（héng）跨障礙，溝壑寬度應不大於Lc+2r，為安全起見，設計溝壑（hè）寬度S 滿足

1.3 目標規劃模型建立

1.3.1 目標（biāo）規劃模（mó）型定義

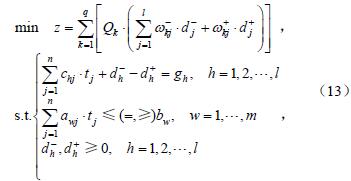
1.3.2 決策變（biàn）量

機器人跨越障礙的決策變量可以分為2 類（lèi），結構（gòu）參數和越障過程參數。結構參數主要是機器人本身（shēn）結構影響障（zhàng）礙跨越的（de）幾何（hé）尺寸，包括驅動輪O1 和（hé）被動輪O2 中心間距Lc，擺臂最大長度La 和驅（qū）動輪半徑r 。越障過程參數主要指越障過程中的x 軸與水平麵夾角β，則可知決策變量X 為

1.3.3 目標函數及目標約束

假設實際的最高（gāo）台階（jiē）為H0，最寬溝壑為S0，由於攀爬台階和跨越溝（gōu）壑均為越障性能，取同一優（yōu）先級，則標函數為

式中wv 為權重，d1+為超過 H0 的（de）部分，d1−為未達到 H0的部分；d2+為（wéi）超過S0的部分，d2−為未達到S0的（de）部分（fèn）。

目標約束（shù）為

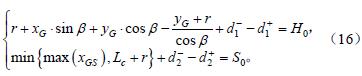
1.3.4 絕（jué）對約束

根據機器人越障過（guò）程需要滿足的（de）要求以及對變量的估計可以確定模型的絕對約束條件，即必須滿（mǎn）足的條（tiáo）件（jiàn）。

1）越障初始條件約束

機器人若能（néng）夠（gòu）順利跨越障礙，則在準備階段（duàn），機（jī）器人擺臂必須能夠與台階邊界線接。

設在跨越障（zhàng）礙（ài）前，與障礙接觸時擺臂行星輪（lún）中心能達到（dào）的最大高度為h0，則根（gēn）據橢（tuǒ）圓定義可知，當行星輪中心與焦點連線垂直於地麵時，存（cún）在最大值

2）不打滑約束

考慮圖3e 所示（shì）臨界狀態處於靜平衡，結合式（4）可得

由於摩擦係數f≤1，因此β 的取值不（bú）超過45°，該約束條（tiáo）件可以用於確定邊界約束。

3）邊界約束

邊界約（yuē）束即為（wéi）對初始解的估計範圍，給定（dìng）初始條件可（kě）以減少計算時間（jiān），提（tí）高效率，邊界約束一般形（xíng）式（shì）為

1.4 模型求解

1.4.1 目標規劃模型求解方法

對於目（mù）標規劃問題，根據其目標函數以及約束條件是否均為線性，可分為線性（xìng）規劃問題和非線性目標規劃問題（tí）。本文建立的模型包含非線性約束條件，屬於非線性（xìng）目標規（guī）劃問題（tí）。對於非線性目標規劃問題，比較傳統的求解方法是線性化逼近算法和模（mó）式（shì）搜索[16]等（děng）。線性化逼近算法（fǎ）對非線性（xìng）方程的處理（lǐ）比較複雜並且容易產生較大誤差。模式搜索僅能給定一組迭代（dài）初值，效率較低（dī）。由於遺傳算法多點並行（háng）搜索的高效性（xìng）和準確性[17]，采用該種方法求解模型。

1.4.2 遺（yí）傳算法的求解過程

遺傳算法是一種基於自然選擇（zé）原（yuán）理和自然遺傳機製的搜索（尋優（yōu））算法，它是（shì）模擬自然界中的生命進（jìn）化機（jī）製，在人工係統中實現特定目標的優化。其實質是通過群體搜索技（jì）術（shù），根據（jù）適者生存的（de）原則逐代進（jìn）化，最終（zhōng）得到最優解或（huò）準最優解（jiě），已經在工程（chéng）領域（yù）得到廣泛應用。其基本流程如下：

1）編（biān）碼及初始化種群。將解變量在邊界約束範圍內映射為遺傳空間的二進製編碼，每個二進製編碼稱為一個個體（tǐ），每個個體對應所求變量的一組（zǔ）解，並隨機產生N個初始個體作為初始種群。

2）個體的（de）適應（yīng）度評價。利用適應度函數判斷解（個體（tǐ））的優劣性，並（bìng）作為選擇較優解的依（yī）據。

3）新種群的產生。通過選擇、交叉和變異產生新的種群個體。

4）終止條件判斷。當進（jìn）化代數小於設定代數時，返回2）繼續運算（suàn）；當進化代數達到設定（dìng）值時，以進化過程中得（dé）到的適應度值最大的個體作為最優解，並終止運（yùn）算。

1.4.3 約束處理

遺傳（chuán）算法在產生新個體時隻能保證產生的個體在所給（gěi）邊界約束範圍內，對於在（zài）邊界約束範圍內（nèi），但是不滿足初始（shǐ）條件約束和不打滑約束（shù）等非邊（biān）界約束的個體沒有得到任何處理。如果直接將其剔除，不但會影（yǐng）響種群數量而且解中的優良基因（yīn）也將（jiāng）得不到保留，為此筆者引入罰函數，降低此類（lèi）解的適應度值。由（yóu）於式（18）可（kě）以通過初始條（tiáo）件限製表示，因此隻考慮（lǜ）式（17）的罰函數g(X)為

式中M 為較大的常數值。

2、模型驗證

2.1 仿真驗證方法

由於機器人所用履帶屬於柔（róu）性體，對於該機器人的仿真屬於剛柔混合仿真，因此建立該機器（qì）人（rén）仿真平台的關鍵是建立合適的履帶模型。對於柔性履帶仿真模型有有限元法和剛體分塊法2 種建模方式，考慮到有（yǒu）限元法對計算機硬件的要求比較（jiào）高，並且計算速度慢，本文采（cǎi）用後者，即建立一係列剛體，各剛體間通（tōng）過旋（xuán）轉副連接形成整條履帶。

目前，可對履帶進行分塊仿（fǎng）真（zhēn）的（de）比（bǐ）較流行的軟件是RecurDyn 和Adams。RecurDyn 自帶Track(LM)履帶仿真模（mó）塊，但是該模塊適用於大型工程（chéng）機械，對於（yú）像本文提出的機器人使用的履帶，履帶標準中沒有相（xiàng）應型號，對於驅動輪及履帶（dài）參數的調試沒有規律可循，筆者最初使用該（gāi）模塊建立仿真模型，雖然可以進行仿真，但是履帶參數（shù）等仍有不合理處，使得仿真時（shí）間很長。此外，如（rú）果改變（biàn）機器人結構，仍舊需要對參數進行（háng）調整，費時費力（lì）。Adams 的帶傳動（dòng）模塊Belt 可用於履帶的仿真，但是它的履（lǚ）帶塊是通過平麵副連接，仿真過程中總是（shì）出現履（lǚ）帶（dài）塊與塊之間（jiān）間距過大情況。為（wéi）此，筆者使用（yòng）Adams/view 二次開發功能，建（jiàn）立機器人的動力學仿真平台，使用鉸鏈連（lián）接相鄰的履帶塊，並使用STEP 函數驅動機器人運動以驗證其性能。

2.2 試驗驗證方法

通過仿真（zhēn）驗證，初步（bù）確定了機器人結構（gòu）參數的可行性，但是仿（fǎng）真環境與實際環境相比是一種比較理想的環境，得（dé）到的（de）機器人結構參數在實際環境的可行性需要（yào）進一步的驗證。

如果按照求解得到的機器人結構參數（shù）設計的樣機能夠跨越160 mm 高的台階和300 mm 寬的溝（gōu）壑，就能保（bǎo）證機器人對核潛艇內（nèi）環境的適（shì）應性，同（tóng）時也能驗證提出（chū）的基於（yú）目標規劃的機器人結構參數設計（jì）的可行性。

為此，筆者按照計算（suàn）得到的機器（qì）人結構參數，使用（yòng）SolidWorks 對機器人的機械（xiè）結構進行了設計，並在（zài）中國科學（xué）院沈陽自動化研究（jiū）所機器（qì）人學國家重（chóng）點（diǎn）實驗室完成了加（jiā）工（gōng）及裝配，如（rú）圖5 所（suǒ）示，機器人（rén）主要由行星輪1、擺臂2、驅動輪3、凸輪4、履帶5、被動輪6、驅動輪電機7、蝸輪蝸杆8、擺臂電機9 以及齒輪10 等組成。

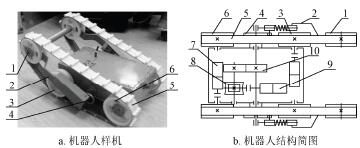
1.行星輪 2.擺臂 3.驅動輪 4.凸（tū）輪 5.履帶 6.被動輪 7.驅動輪電機 8.蝸（wō）輪（lún）蝸（wō）杆 9.擺臂電機 10.齒（chǐ）輪

圖5 機器人樣機（jī）及結構（gòu）簡圖

考慮到空間的緊湊（còu）性以及可行性，機器人采用電機經減速器減速後直接驅動的方式。由於擺臂擺動過程中需要撐起機體，需要的力矩較大（dà），並（bìng）且考慮（lǜ）到自鎖性能的需要，在經過減速器後采用蝸輪蝸杆傳動。由於機器人（rén）機（jī）體長度僅有290 mm，如果蝸輪直接（jiē）安裝於擺臂軸，擺臂電機的安裝空間僅有機體的一半，很難容納下整個電機（jī），為此經蝸輪蝸杆（gǎn）傳（chuán）動後增加齒輪傳動將扭矩輸出到（dào）擺臂軸，如圖（tú）5b 機器人結構簡圖所示。

2.3 結果與分析

2.3.1 機器（qì）人機構參數理論計算結果

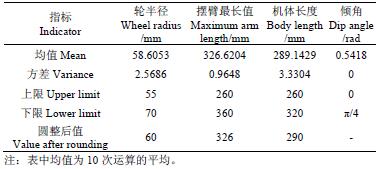
根據對（duì）核潛艇實際環境的測量，可以得到環境中最高（gāo）台階H0=160 mm，最寬溝壑S0=300 mm。由（yóu）於所取目標均（jun1）是越障性能目（mù）標，則設定為同一優先等級且權重相等。根據（jù）環（huán）境中障礙大小以及對機（jī）器（qì）人的要求，對（duì）所求取的參數進行了估計，各設（shè）計變量的估計上下限如表1所示。

表1 設計（jì）變量上下（xià）限（xiàn）及優解

計算過程中，種群數量設置為100，進化代數為100，交叉概率為0.07，變異概率為0.005。應用MATLABR2013a 完成了求解算法程序的編寫，並對程（chéng）序運行10次，以期（qī）獲得最優（yōu）參數。

由於初始種群的隨機性，以及（jí）進化代數的影響，加之（zhī）計算中保留小數後4 位的精度，多次運行得到的結果會存在微小的波（bō）動（dòng），為此（cǐ）取10 次計（jì）算結果的均值（zhí）作為結構（gòu）參數的參考值，並將數值圓整，可得到機器人的結構參數（shù）值：履帶輪半徑60 mm，擺臂最大長度326 mm，機體長度 290 mm，如表 1 所示。此時 d1+ = 0.0923 ，d2 0.3706 − = ，可見，跨越溝壑理論上存在稍微不足，但是由於跨越溝壑過程中僅僅考慮了重心到輪心的距離，對於機器人輪心之外的半徑長度可以（yǐ）彌補d2−這一微小偏差（chà）。為了驗（yàn）證結構參數的可行性（xìng），采用圓整的尺寸，建立動力學仿真平台進行（háng）驗證。

2.3.2 仿真驗證結果

1）攀爬台階仿真驗證

根據對核（hé）潛艇（tǐng）環境障礙的實測值，設置160 mm 的台階障礙，並利用Adams 中的STEP 函數對機器（qì）人的越（yuè）障過程進行規劃，其（qí）越障過程如圖6 所示。

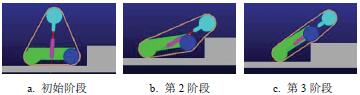
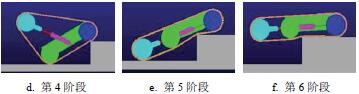
圖6 機器人（rén）攀爬台階仿真

圖6 可知，機器人能順利跨越高度為160 mm 的台（tái）階，從Adams 的（de）後處理模塊Postprocessor 可以得（dé）到攀爬台階過程中（zhōng）驅動輪（lún）以及擺臂所需的驅動力（lì）變化情況，如圖7所示。越障過程中擺臂需要的驅動力矩最大為21.4653N·m，驅動輪所需驅動力矩最大為5.604 N·m。

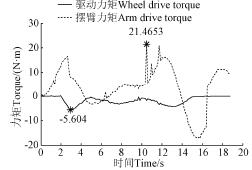
注：-5.604 N·m 是驅動輪所（suǒ）需的最大力矩，21.4653 N·m 是擺臂所需（xū）最大力矩。

圖7 機器人攀爬台（tái）階驅動力矩

2）跨越溝壑仿（fǎng）真驗證

同攀（pān）爬台（tái）階類似，根據實際溝壑寬（kuān）度，設置了300 mm寬的（de）溝壑模型，並利用STEP 函數完成了機器人的越障仿（fǎng）真，其跨（kuà）越（yuè）溝壑過（guò）程如圖8 所示。

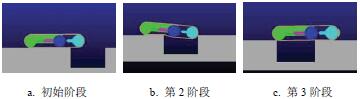
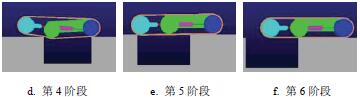
圖8 機器人跨越溝壑仿真

圖8 表明，機器人能順利跨越寬度（dù）為300 mm 的台階，同攀爬（pá）台階類似，可得跨越溝壑過程中驅動輪（lún）以及擺臂所需的驅動力如圖9 所示。由圖9 可知，跨越溝壑過程中擺臂所需（xū）的最大驅動力矩為20.4987 N·m，驅動輪所需的最大驅動力矩為2.842 N·m。

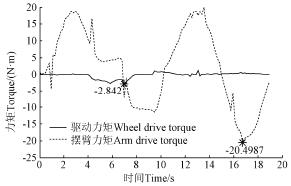
注：-2.842 N·m 是驅動輪所需的最大（dà）力矩，-20.4987 N·m 是擺臂所需最大力矩。

圖9 機器人跨越溝壑驅動力（lì）矩

綜（zōng）上可知，所設計的結構參數能夠適應環境中的障礙（ài），可以進行樣機的設（shè）計，且通過（guò）仿真得到了（le）機器人擺臂以及驅動（dòng）輪所需的驅動力矩，可以指導機器（qì）人設計中電機的（de）選取。同時也初步證明了基於目標規劃的機器人結構參數設計的有（yǒu）效性。

2.3.3 樣機試驗驗證結果

1）攀爬台階

按照核潛艇內環境障礙，布置了高度為160 mm 的台階，機器人的（de）越（yuè）障過（guò）程如圖10 所示。首先（xiān）使機器人前行直至擺臂處履帶與障礙接觸（圖10a）；再控（kòng）製擺臂向有障礙方向擺（bǎi）動支撐起機體（圖10b），同時使機器人緩慢前（qián）行，當機體部分履帶與障礙接觸後（圖（tú）10c），使機器人停止（zhǐ）前行（háng），僅控製擺（bǎi）臂向後擺動直至擺臂撐（chēng）起機器人（圖10d～圖10e）；此時（shí），停止對擺臂的控製，驅動機（jī）器人前行，最（zuì）終機器人能夠順利攀爬台（tái）階（圖（tú）10f）。

圖10 機器人攀爬台階試驗

按照以上步驟（zhòu）進行了多次攀爬台階試驗，機器人均能（néng）順利跨過障礙值。並且將台階高度增加到170 mm 進行試驗，機器人仍舊順（shùn）利跨越了障礙，當增加到180 mm 時機器人沒能（néng）越過障礙。

可見（jiàn），實際（jì）設計的機（jī）器人滿足環境（jìng）中台階障礙的要求，並且能攀爬的台階高度（dù）超出預期高度相對也較小，這證實了基於目標規劃（huá）的機器人結構參數設計（jì）的可行性。對於超出部分（fèn）可能（néng）是由於實際加工以及裝配中的偏差所致，也可能是由於履帶是柔性體，在與障礙接觸過程中，產生微小形變引（yǐn）起的。因為履帶（dài）的微小形變會增大機器人與障礙之間（jiān）的摩擦力並且使得在跨越障礙過（guò）程中的關鍵狀態（圖3e）機器人的重心更低更穩定，而在參數計算過程中並沒有考慮履帶變（biàn）形的影響。

2）跨越溝壑（hè）

同攀爬台階類似，根據環境要（yào）求設置了300 mm 寬的溝壑進行試驗驗證，機器人越障過程如圖11 所示。首先驅動擺臂轉動，同時驅動機器人緩慢前行，直到機器人機體橫跨溝壑（hè），再使擺（bǎi）臂後擺直至與地（dì）麵接觸，然後驅動機器人前行，最終機器（qì）人順利跨（kuà）越了300 mm 寬的溝壑。同樣將溝壑每次增（zēng）寬10 mm 進行（háng）多次試驗（yàn）過程中發現，當溝壑增（zēng）大到330 mm 時機器人沒能跨越（yuè）溝壑。這主要是因為（wéi）在理論計算中，為了安全起（qǐ）見，取圖4b 中（zhōng）的條件滿足Lc+r 而不是Lc+2r 所致。

圖11 機器人跨越溝壑試驗

通過以上試驗，充分驗證（zhèng）了機器（qì）人對環境障礙（ài）的適應性（xìng），並且超出預期跨越障礙（ài）值也較小，也證明了基於目標規劃的機器人結構參數設計方法的（de）有效性。

3、結（jié）論與討論

針對差異化障礙環境下的機器人結構（gòu）參數（shù）設計問題，提出了基於目標規劃的機器人結（jié）構參數（shù）設計方（fāng）法。通過建立機器人（rén）結構參數（shù）與環境障礙之間的函數關係，得到機器人越障的性能（néng）函數，結合需要跨越的障礙值，建立目標規劃模型，然後利用遺傳算法求解得到最優的結構（gòu）參數值：履帶輪半（bàn）徑60 mm，擺臂最大長度326 mm，機體長（zhǎng）度290 mm。經試驗驗證，利用得到的參數設計的（de）機（jī）器人能夠跨越160 mm 高台階和300 mm 寬溝壑，並且能跨越的最高台階和最寬溝壑與期望（wàng）值相差較小。該（gāi）方法（fǎ）能夠得（dé）到適應該環境的機器人結構參數的盡可能小的值，不（bú）但可以減少機器人設計成本，還可以（yǐ）保證機器人在滿足環境要求的前提下盡可能的輕便。此外，該方（fāng）法也可以用（yòng）於其他環境障礙要求下（xià）的其他類型（xíng）機器人的（de）結構參數設（shè）計。

本（běn）文提（tí）出基於目標規劃的機器人結構參數設計的最初目的（de）是使得設計的機器人剛好（hǎo）能滿足（zú）環境中障（zhàng）礙的要求（qiú）。但試驗過程中發現，機器人實際能跨（kuà）越的（de）障礙稍大於預期的障礙，可能的主要原因是（shì），在參（cān）數計（jì）算時（shí）沒（méi）有考慮履帶的形變對（duì）越障的影響，因此，下一步計劃對履帶形變對機器人（rén）越障性能的影響進行研究。

投稿箱：
如果您有機床行業、企業相關新（xīn）聞稿件（jiàn）發表，或進行資訊合作，歡迎聯係本網編輯部，郵箱（xiāng）：skjcsc@vip.sina.com

更多相（xiàng）關信息

名企推薦

業界視點

| 更多

行業數據（jù）

| 更多

博文（wén）選（xuǎn）萃

| 更多

數（shù）控機（jī）床