可轉位刀具的動態可靠性靈敏度（dù）研（yán）究-刀具網-數控機床市場網

您現在的位置（zhì）：刀具網> 技術（shù）前沿（yán）>可轉位刀具的動態可靠性靈（líng）敏度研究

可（kě）轉位刀具的動態可靠（kào）性靈敏度研究

2016-1-21 來源（yuán）：東北大學（xué）機械工程與自動化學院（yuàn）秦皇島分校作（zuò）者：王新剛呂春梅逄旭王（wáng）雪玲（líng）

摘要: 可轉位刀具在斷續切削加工時，其主要失效形式（shì）是疲勞破損（sǔn）．刀具各設計參數的選取直接影響刀（dāo）具（jù）的可靠度．以應力－強度幹涉模型為基礎，建（jiàn）立了可轉位（wèi）刀具的（de）動態可靠性數學模型，給出了刀具在切削加工時的可靠度變化規律．在此基礎上與靈敏度分析方（fāng）法相結合，推（tuī）導了刀具各設計參數的動態可（kě）靠（kào）性靈（líng）敏度計算公式，並（bìng）給出了各設計參數的動態可靠性靈敏度的變化（huà）曲線（xiàn）．研究表明，刀具各設計參（cān）數的改變對其可（kě）靠性的敏感程度大小不一（yī），對敏感（gǎn）參數的選取要加以控製，以提高（gāo）刀具的可靠度和被加工零件（jiàn）的精度．同時為提高刀具係統及（jí）整個機床的（de）可靠性提（tí）供理論（lùn）依（yī）據．

關（guān）鍵詞: 刀具; 失效率; 動態可靠性; 靈敏度; 臨界（jiè）疲勞應（yīng）力

在現代化自動加工技術中（zhōng），切削加工（gōng）刀（dāo）具要求具有高效、耐（nài）久、可靠和經濟的特點，尤其是在NC，MC，FMS 等自動化加工中，可靠性顯得更加突出（chū）．如果刀具可靠性差，可能增（zēng）加換（huàn）刀時間或者產生（shēng）廢品，損（sǔn）壞機床和設備（bèi），甚至造成人員傷亡，所以研究刀具的可靠性及其靈敏度技術迫在眉睫．

李兆（zhào）前等對刀具的可靠性進行了研究，建立了可（kě）靠性模型，並（bìng）通過物理實驗（yàn）給予驗證．董麗華等對刀具切入類型和切削（xuē）力對刀具壽命的（de）影響進行了研（yán）究，並取得一定的成果．Lee 和Kramaruddin 等通過車床模擬斷續切削，證明了刀具切出時要比切入（rù）時的可靠度要低，並提供了令人信服的證據．目前國內外學者大都以研究如何正確選取刀具（jù）切削參數和（hé）刀具幾何參數來達到提高刀具可靠性（xìng）的目的，此研究較成熟，而對刀具的物理（lǐ）性能參數和材料參數對刀具可靠（kào）性的影響程度即靈敏（mǐn）度研究還未見報道．本文（wén）從可靠性的概念出發，結合隨機過程、應力－強度幹涉模型、靈敏度等數學力學方法，建立可轉位（wèi）刀具的動態可靠性（xìng）及靈（líng）敏度（dù）的數學模（mó）型，給（gěi）出刀具物（wù）理參（cān）數和材料參數的靈敏度變化（huà）規律，進一步完善刀（dāo）具可靠性和可靠性靈敏度的（de）理論方法．

1 可轉位刀（dāo）具動態可靠性模型建立

可轉位刀具（jù）切削效率高，輔助時間少，工效較（jiào）高，而（ér）且可轉位（wèi）刀具的刀體可（kě）重複使用，節約了材料和製造費用，進而廣泛應用到 NC 機床（chuáng）上．但由於刀片的材料和製作（zuò）工藝等因素，會導（dǎo）致刀片內部存在著許多微觀裂紋．當刀片工作時，隨（suí）機變化（huà）的切削力，特別是衝擊載荷（hé）不斷作用到刀頭，導致（zhì）刀體內（nèi）部裂紋核發生（shēng）疲勞擴展進而（ér）失效。

為了降低刀具的失效概率，需（xū）要對影響刀具可靠性的敏感參數進（jìn）行分析研究，這就需要建立刀具可靠性和靈敏度分析的數學（xué）模型．可轉位刀具（jù）的失效判據是研究（jiū）刀具可靠性及靈敏度（dù）的基礎，所以本文提出了以 SSI 模型為基礎的考慮衝擊載荷作用次數的刀具可靠性數學模型。

本文設可轉位刀具的刀片有 d 個刀頭，每個刀頭的工作狀（zhuàng）態都是相互獨（dú）立的，那麽整個（gè）刀具的可靠度可以看（kàn）作是由（yóu） d 個並聯的子係統構（gòu）成的可靠度，則可轉位刀（dāo）具的整體可靠度為

設σ為刀具體內某一點應力，σt為刀具臨界疲勞應力．當刀片整體或任意刀頭內的應力超過（guò）臨界疲勞（láo）應力時，刀具就會失效．設第 i 個刀頭（tóu）內的應力分布函數為 Fi(σ);臨界疲勞（láo）應（yīng）力的分布函數和概率密（mì）度函數分別為 Fti(σ)和 fti(σ)．由可靠性的幹涉理論，就可以確定刀具任（rèn）意子係統的可靠度，即

則刀具整體係統的可靠（kào）度為

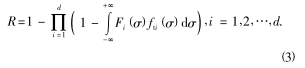
刀具在（zài）加工工件時，由於交變的切削（xuē）力作用使其刀具材料內部裂紋發生疲勞（láo）擴展，當裂紋長度（dù）超過一定尺寸時就發生崩刃．當刀具內部應力沒有達到刀具臨界疲勞應（yīng）力時，裂紋不一定馬上失穩擴展，而（ér）是要衝擊 N 次才能失效，所以考慮衝擊載荷作用次數的等效載荷的（de）累積分布函數為

其概率密度函數為

所以，考（kǎo）慮衝擊載荷作用 s 次的可轉位刀具的可靠度計算公（gōng）式為

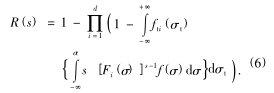
當（dāng） s =1 時，式(6)變為傳統的應力－強度幹（gàn）涉模（mó）型（xíng）．

可轉位刀具在斷續切（qiē）削加工時所受到的衝擊載荷作用次數是隨著加工時間的增加而遞增的，所以衝擊載荷作用過程可用泊鬆隨機過程來描述［9 ］．當衝擊載荷作用次數 N(t) 服從參數為λ(t)的泊鬆隨機過程時，在任意時刻 t 衝擊（jī）載荷出現 s 次的概率可表示（shì）為（wéi）

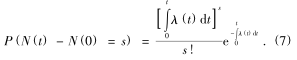
由式(6)，式(7)可知，刀具（jù）在 t 時刻的可靠度為（wéi）

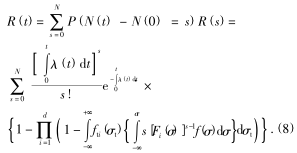
由式(7)可（kě）知，隻（zhī）要確定了臨（lín）界疲勞應力 σt的概率密度函（hán）數 ft(σ)，就可以求出刀具（jù）的動態可（kě）靠度。

可轉位刀具在早期發生破壞時（shí），主要原因是衝擊載荷作用造成的，熱衝（chōng）擊載荷很小（xiǎo）可不計．當刀具在切削工件時，其衝擊載荷主要與切（qiē）削參數(例如切削速（sù）度（dù）與進給量)有關，而熱衝擊載荷主要與（yǔ）切削速度有關．當刀具內部裂（liè）紋尖端應（yīng）力強度因子達到或超（chāo）過其材料的斷裂韌性時而發生斷（duàn）裂．如果刀具材料內部已有某一長度裂紋，那麽對其施加不同的應力時，斷裂裂紋長度也必定不同．當（dāng）對刀具施加 σc的應力時，沒有發裂紋擴（kuò）展即（jí）斷裂，這時必定（dìng）

式（shì）中:aei， ac為裂紋（wén）長度;KIC為平麵（miàn）斷裂韌性;Y裂紋形狀因子;σc為應力（lì）對於該裂紋，如果施加其他的切削應（yīng）力 σt(σt＜ σc)時，刀（dāo）具不一定立即（jí）失效，而是要衝擊N 次才能失效，即

式中（zhōng）: a 為裂紋長度;N 為衝擊次數，即刀具（jù）壽命;n，A 為刀（dāo）具材料參數;ΔKI為等效應力強度因子幅值．當切削力在最小與最大幅值之間變化時，有

對式(10)積分，得

式中，acl為施加 σt時裂紋的斷裂尺寸，當 aclaei時，則有

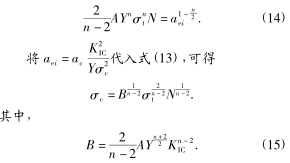
由（yóu）文獻［11］可知材料的抗拉強度服從威布爾分布，所以其概率密（mì）度函數為（wéi）

式中（zhōng）:V 為試件體積;mt，σt 0，σtu分別為抗拉強度的形（xíng）狀（zhuàng）參數（shù）、比例參數和位置參數．結合式(15) ～式(16)，可（kě）得臨界疲勞應力的概率密（mì）度函數，即

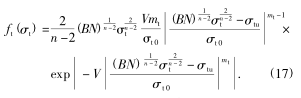
將式(17)代入式(6)即可得考慮衝擊載荷作用 s次的可轉位刀具的可（kě）靠度函數為

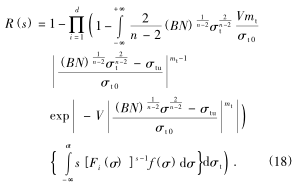
將式（shì）(17)代入式(8)可得考慮刀片切削（xuē）加工時間的可轉位刀具的動態可靠度函數為

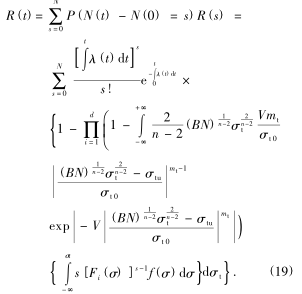
2 可轉位刀具的動態可靠性靈敏度分析

本文假設基（jī）本隨機變量向量 X =( nAKICVσt)T，各基本（běn）隨機變量是相互獨立的，基本隨機變量（liàng）向量 X 的均（jun1）值 E(X)是已（yǐ）知的．考慮衝擊載荷（hé）作用次數下的刀具的（de）動態可靠性（xìng）靈（líng）敏度為式(20);考（kǎo）慮刀具切（qiē）削加工時（shí）間的刀具的（de）動態（tài）可靠性（xìng）靈敏度（dù）為式（shì）(21):

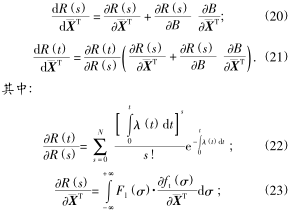
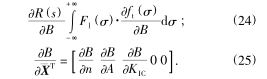
當某參數（shù）的可靠性靈敏度數值為正值時（shí），說明隨著該參數均值的增加，其結果將使刀具趨於更（gèng）加可靠．而當某參數的可靠性靈敏度數值為負值時，則說明隨著該參數（shù）均（jun1）值（zhí）的增（zēng）加，其結（jié）果將使刀具趨於更加（jiā）不可靠(失效)．對可靠性靈敏度（dù）絕對數值較大的參數，其變化率較大，對刀具的可靠度最為敏感，在參數選取時應加（jiā）以控製，以提高刀具的可靠度和被（bèi）加工零件的精度．

3 測試與有限元（yuán）分析

測試（shì）條件:數控機床 CL－15;工件材（cái）料:45#淬硬鋼;HＲC (51－52);工件組裝後外圓直（zhí）徑（jìng）130 mm; 刀（dāo）片（piàn）型號: SNGM150608; 密度 ρ =5 500 kg /m3;彈性模量 E = 450 GPa;泊鬆比 μ =0. 25;HＲA (92. 5);刀具幾何參數:mc= 0. 25，Kr=75°;切（qiē）削（xuē）用量:v = 2 mm /s，f = 0. 15 mm /r，ap=0. 5 mm．通過三（sān）向測力儀係統、電荷放大器、接線（xiàn）端子板、數據采（cǎi）集卡和切削力（lì）數據（jù）處理係統，測（cè）出切削力，然後利用有限元求出刀片內的（de）應力分（fèn）布，同時記錄衝擊載荷作用（yòng）的時間（jiān）及出現（xiàn）的頻次．刀片的（de）應力雲圖如圖（tú） 1 所示．

每加工 1 min 對刀片進行一次檢測，以裂紋長度為 0. 06 mm 為裂紋萌生階段．當裂紋長度大於 0. 06 mm 時為疲勞（láo）裂紋擴展階段．通過掃描電鏡及超聲波檢測來確（què）定裂紋的尺寸及相應參數，再通過（guò）式(9) ～式(17)來確定臨界疲勞應（yīng）力的概率密（mì）度函數。

通過測（cè）試與分析，在斷續切削過程中所受到的衝擊載荷作用次（cì）數與時間的（de）關係（xì）服從參數為λ(t) = 23 min－1的泊（bó）鬆隨機過程;通過有限元分析可知刀片內部危險位置的應力（lì）大（dà）小服從均值E(σ) = 730 MPa，方差 Var(σ) = 55 MPa 的正態分布;刀片抗彎（wān）強度服從參數為(4. 02，156. 8，790)的三參數（shù）威布爾分布．刀具其（qí）他設計參數為KIC= (13，0. 06) MPa·m1/2，A = (8. 6 × 10－15，4. 6 ×10－26)，Y = (1. 35，0. 76)，n = (13，1. 6)，V = (1. 3， 0. 68)mm3，刀（dāo）具（jù）壽命 N = 15 000．衝擊載荷作用次數下的刀具對各參數的（de）動態可靠性靈敏度（dù）如圖 2 所示;基於切（qiē）削加工時間的刀具對各參數的動態可靠性靈敏度如圖 3 所示．

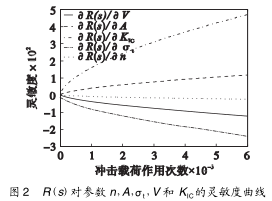
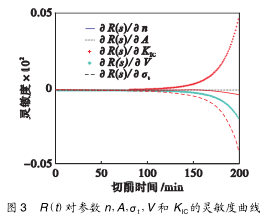
從圖 2 ～圖 3 中可以看出，隨著衝擊載荷作用次數（shù）和切削加工時（shí）間的增加，各（gè）參數的靈敏度也逐（zhú）漸（jiàn）增大．Ｒ(s)和（hé）Ｒ(t)對參數 A 和 KIC的靈（líng）敏度大於零，隨著參（cān）數 A 和 KIC均值的（de）增加，將使刀（dāo）具趨於更加可靠．從圖 2 中可以看出 KIC的靈敏度數（shù）值最大，為最敏（mǐn）感（gǎn）的參數．而 n，V，σt的靈敏度小於零，隨其均值的增加將使刀具趨於不可（kě）靠（kào）(失效)．工程設計人員從圖 2 ～圖 3 中可以迅速地確定影響（xiǎng）刀具可靠度的參數，並對該參數進行直接或過（guò）間接的控製，例如參（cān）數 V 和 σt可通過改變切削用量來直（zhí）接實現參（cān）數的控製;KIC， n 和 A可通過間接改變切削環境溫（wēn）度、切（qiē）削液（yè）和介質以及（jí）刀（dāo）具幾何尺寸來實現參數（shù）控製等（děng），以（yǐ）便保證（zhèng）刀具（jù）在工作時的高可靠度．

4 結論

1) 本文提出考慮衝擊（jī）載荷作用次數和切削加（jiā）工時間的（de）可轉位刀具的動態可靠性（xìng）及動態（tài）可靠性靈敏度計算方（fāng）法，研究刀具各參數的變化對其整體（tǐ）結構可靠性的影響程度，為合理的確定刀具設計參數奠定了理論基礎。

2) 隨著切（qiē）削加工時間和衝擊載荷作用次數的增加，刀具對各參數的（de）敏感程（chéng）度也逐步增（zēng）大．特別是（shì）σt和 KIC敏感參數的變化將對刀具（jù）的可靠度產生（shēng）較大的影響．通（tōng）過直接或間接改變切削條件、環境溫度和介質等（děng）手段對敏感參數應加（jiā）以控製，以提高刀具的可靠度。

3) 本文提出的刀具失效（xiào）判據（jù）和理論算法適用於其他類型刀具的可靠性及靈敏度分析。同時算例給出的刀具物理參數和材料參數的靈敏度排序結果也適用於同類材料刀具參數的靈敏度分析。

投稿（gǎo）箱（xiāng）：
如果您（nín）有機床行業、企業（yè）相（xiàng）關新聞稿件發表，或進行資訊合作，歡迎聯係本網編輯部，郵箱：skjcsc@vip.sina.com

更多相關信息

名企推（tuī）薦

業界視點

| 更多

行業數（shù）據

| 更多

博文選萃

| 更多（duō）