0 前言

     結合部（bù）的動態特性參（cān）數是（shì）影響機床整機動力學性能的關（guān）鍵因素。根（gēn）據統（tǒng）計，機床中出現的振動問題有60%以上是源自結合部[1]，因此，結合（hé）部動態（tài）特（tè）性參數分析一直是國內外學術界研究（jiū）熱（rè）點。直線（xiàn）導軌已廣（guǎng）泛（fàn）地應用於現代數控機床，圍（wéi）繞其動態參數建模，國內外學者已做了大量的有益工作，其研究方法概括起來有三種:

      ① 試驗測試法。該方法主要通過錘擊（jī）試驗分別測定導軌豎直方向和（hé）水平方向的（de）傳遞函數，再根據模態理論（lùn）識別出兩（liǎng）個方（fāng）向的剛度、阻（zǔ）尼係數，從而獲得直線導軌結合部（bù）的動力學參數[2-3]。也有學者將直線導軌整體結構（gòu）離散為（wéi）若幹個子結構或（huò）子係統，通過試驗測試的方法得到（dào）各個子係統的剛度矩陣和阻尼（ní）矩陣，再將各個子（zǐ）結構的運動方程綜合起來，從而得到整個係統的運動方程和動（dòng）力學特性[3-5]。② 理論計（jì）算法。該方法主要以結合（hé）部的基（jī）本（běn）特性（xìng）參數為基礎，簡化結合部模型（xíng），求得結合部（bù）各處的剛度和阻尼，或者通過（guò）有限元分析方法，得到導軌結合部的特性參數[1，6-9]。③ 試驗測試與理論計算相（xiàng）結合方法。該方法首先通過（guò）試驗方法測試導軌結（jié）合（hé）部的（de）動力學參數，然後再用有（yǒu）限元（yuán）方法求解，為機床的動態設計提供一（yī）種有效的方法[10-13]。然而，上述研究工作（zuò）存在兩方麵（miàn）問題：① 傳統直線導軌結合部模型，全部忽略了作為直線導軌必要部件——滾珠絲杠副對結合部動（dòng）態特性參（cān）數的影響，因此，所建立的模型不能很好地描述直線導軌副的動態特（tè）性；② 試驗測試法需要搭建較為複雜試驗裝備，而有限元法（fǎ）建模較為繁瑣，且依賴於大型商用軟件。

     本文以帶滾珠絲杠副（fù）直線導軌結合部為研究對象，借助於彈性力學中（zhōng）的赫茲接（jiē）觸理論，分析計算直線滾動導軌的線剛度、滾珠絲杠副（fù）和（hé）角接觸滾（gǔn）動軸承的軸向剛度，建立帶滾珠絲杠副的機床直線導（dǎo）軌結合部（bù）的（de）動力學模型。通過一款帶滾珠絲杠副的直線導軌結合部的立式加工中心的整機動態特性分析，驗證了提出的結合（hé）部動態特（tè）性模型的有效性和可行性。

1 結合部動力學建模

     圖1 為數控機床（chuáng）典型的直線滾動導軌進給係統的結構示意圖，通過滾珠絲杠副和直（zhí）線導軌副的組合來實現工（gōng）作台x 方向（xiàng）的進（jìn）給（gěi）運動。

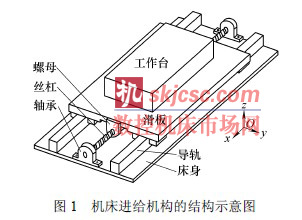
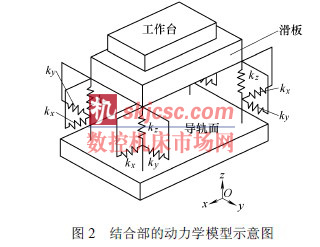
      圖2 為帶滾珠絲杠（gàng）副（fù）的直線滾動導軌結合部的動力學模型（xíng），結合部的（de）x 向剛度為滾珠絲杠副的軸向（xiàng）剛度，y 向剛度為直線滾動（dòng）導軌的橫向剛度， z 向剛度為直線滾動導軌的垂向剛度（dù），並且每個方向上的剛度值均（jun1）由四組彈簧等價模擬（nǐ）。因此，隻須（xū）計算（suàn）出滾珠絲杠副的軸向剛度、直線滾動導軌的橫向剛度（dù）和垂向剛度（dù），便可確定結合（hé）部（bù）的動態特性參數。

     現假設如下所述。

     (1) 忽略表麵粗糙度對（duì）結合部剛度特性的影響。因為帶（dài）滾珠絲杠直線導軌結合部的接觸副均為（wéi）高副，在預緊載荷或工（gōng）作載（zǎi）荷的作用下，其接（jiē）觸區彈性變（biàn）形量可達到數個微（wēi）米(一般（bān）在2～7 μm 之間)，遠遠大於滾道或滾珠的表麵粗糙度(一般小於0.08μm)[14-15]。因此（cǐ），在（zài）計算接觸剛度（dù）時，可不考慮表麵粗糙度的影（yǐng）響，進而可忽略材料塑性變形的影響。

     (2) 滾（gǔn）珠與滾道接觸時（shí）隻產生彈性變形，並服（fú）從Hooke 定理。在正常情（qíng）況下，帶滾珠（zhū）絲杠直線導（dǎo）軌（guǐ）結（jié）合部各接觸副變形均在材料彈（dàn）性範圍內，接觸點處產生的塑性變形量不超（chāo）過滾動體直徑的萬分之一(遠小於接觸副彈性變形量)[16]。因此，滾珠（zhū）與滾道接觸隻考慮彈性變形的假設，在分析帶滾珠絲杠副直線導軌結合部剛度（dù）時是適宜的。

    1.1 滾珠絲杠副軸（zhóu）向（xiàng）剛（gāng）度的計算

     滾珠絲杠副的軸向剛（gāng）度kx 為與滾珠絲杠副相關聯的零部件剛度的（de）串聯總和[17]，其（qí）中以（yǐ）絲杠、螺（luó）母組件和支承軸承的軸向（xiàng）剛度影響最大（dà），其他（tā）零部件的影響（xiǎng）較（jiào）小，可忽略不計（jì），其動力學模（mó）型如圖3所示。

     顯然，進給絲杠傳動係統的軸向剛度kx 可表示為

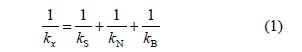
     式中 kx ——滾珠絲杠副（fù）軸向剛度

kS ——絲杠軸向剛度

kN ——螺母組件軸向剛度

kB ——支撐軸承軸向剛度

      1.1.1 絲杠（gàng）的軸（zhóu）向剛度

     滾珠絲杠軸向剛度的計（jì）算，隨滾珠絲杠的支承方式不同而存在著（zhe）差異。限於篇幅，本文隻討論兩端固定（dìng）支承結構（gòu）方式(圖4)，這也是滾珠絲杠副最為（wéi）常見的（de）一種支承形（xíng）式，並不失一般性。

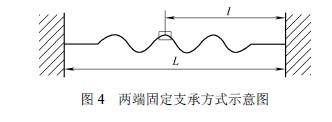
     可由材料力學（xué）得到其軸向剛度為[18]

     式中 d ——絲杠的螺紋底徑

           l ——載荷作用點至右端軸承的距離（lí）

           E ——絲杠材料的縱向彈性模量

      當（dāng）螺母處於絲杠中間位置時，絲杠軸向剛度kS的值（zhí）為最小，即

      本文以絲杠的最小剛度kSmin 作為其軸向剛度值。

      1.1.2 螺母組件軸向剛度的計算

      螺（luó）母（mǔ）組件軸向剛度（dù）可由作用在螺母上的軸向載荷除以其軸向（xiàng）變形量求得，即

      假設如下：① 負荷垂直於接觸表麵（miàn），也就是說，接觸表麵完全光滑，不計及滾珠與滾道麵間（jiān）的摩擦力；② 滾珠與滾道接觸麵（miàn）的尺寸與其曲率半徑相比是很小的；③ 考慮到（dào）滾珠絲杠副的工作轉速一般都較低，在分析過（guò）程中不考慮滾（gǔn）珠離心力和陀（tuó）螺力矩的影響；④ 不（bú）考慮由於製造誤差（chà）所產生的影響，即軸（zhóu）向工（gōng）作載（zǎi）荷（hé）均勻（yún）地分配給每個滾珠。在（zài）以上假設下，螺母組件的軸向變形量完全由滾珠與滾道麵的彈性接觸變形所引起，可利用赫茲彈性接觸理論來進（jìn）行理論計算。其計算過程（chéng）主要可分（fèn）為（wéi）以下幾（jǐ）個步驟。

      滾珠與螺母或絲（sī）杠（gàng）滾道（dào）麵的法向接觸變形量的計算。根據赫茲接觸理論，兩（liǎng）彈性體（tǐ）由於彈（dàn）性變形引起的相（xiàng）對（duì）位移量(彈性接近量)為

     滾珠與螺母（mǔ）滾道接觸點處的4 個主曲率（lǜ）分別為

      當已知τ值便可（kě）通過查表得到（dào）J 和ma 的值[20]。至此，隻要（yào）將J、ma 以及Σρ 和（hé）p 的值代入式(5)，即（jí）可得到δ 的值（zhí）。

      (2) 單個滾（gǔn）珠軸向變形（xíng）量的計算。單個滾珠在法（fǎ）向接觸壓力p 作用下而產生彈性（xìng）變形如圖5 所示，由滾珠（zhū）法向彈性接（jiē）觸變形所（suǒ）產生的（de）法向彈性位移量

      δp 為

δ p =δ1 +δ 2        (15)

     (3) 單個滾珠法向接觸力的計算（suàn）。雙螺母預緊結（jié）構(圖6)是滾珠絲杠最（zuì）為常見（jiàn）的（de）預緊方式，其螺母組件軸向剛度的計算方法如下。

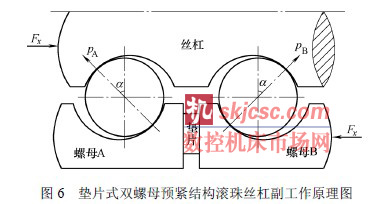
      假定滾珠絲杠副中螺母A上每個滾珠給予絲杠滾道（dào）麵的法（fǎ）向作用力為pA，螺母B 上每個滾珠給予絲杠滾道麵的法向作用（yòng）力為pB，且預緊墊片通過螺母A、B 給予絲杠的預緊（jǐn）法向力為pP。則由絲杠（gàng）靜力平衡可得（dé）

Fx − pA z sinα cosφ + pBz sinα cosφ = 0            (17)

      在軸向載荷Fx 作用下，螺母A 相對絲杠所產生的軸向彈性接觸變形量δA 應恰好等於螺母B 相對於絲杠（gàng）所產生的軸向彈性恢（huī）複量。

      由力學疊（dié）加原理可知，作用於（yú）同一物體的合力所產生的變形，應等於各分力在同方向上所產生（shēng）的變形量之和；又由赫茲接（jiē）觸理論可知（zhī），兩彈性（xìng）體的彈性趨近量與其法向壓（yā）力的2/3 次方成（chéng）正比的關係（xì），於是有

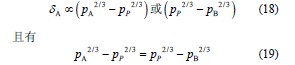
      當已知Fx 和（hé）pP 時，可由式(17)和式(19)聯合求解得到pA 和pB 的（de）值。

      得到了單個滾珠的法向接觸（chù）力後，便可由（yóu）式 (5)～(16)求（qiú）得螺母A 相（xiàng）對於絲杠所產生（shēng）的軸向變形量δA，也即軸（zhóu）向載荷Fx 沿軸（zhóu）向（xiàng）的位移量δN，並最終由（yóu）式(4)獲得螺母組件的軸向剛度kN。

      1.1.3 支承軸承的軸向剛度計（jì）算

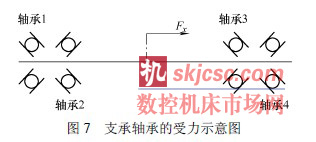
     試驗（yàn）表明，軸承的變形量占整個傳動係統總變形量的50%以（yǐ）上[20]。本文以數控機床常用的一對角接觸球軸（zhóu）承，背對背安裝的結構（gòu）為例(圖7)，進行軸承剛（gāng）度計算。之前螺母（mǔ）組件軸向剛度計算的假設條件，仍然適用於軸承軸向剛度的計算，在此（cǐ）不再贅述。與螺（luó）母組件軸向剛度的計算過程類似，軸承軸向剛度的計算也可（kě）以（yǐ）分為三步。

      (1) 利用式(5)～(14)計算滾（gǔn）珠與內圈或外圈（quān）滾道麵的法向接觸變形量。

      (2) 利用式(15)和式(16)計（jì）算單個滾珠（zhū）的軸向變形量。

      (3) 單個滾珠法向接觸（chù）力的計（jì）算。

      假定各軸（zhóu）承中單個滾珠所受的（de）法向接觸力分別為p1、p2、p3 和p4，顯然p1= p3，p2= p4。由於軸（zhóu）承預緊而使其（qí）單個滾珠承受的（de）法向力（lì）為p0。軸承1、2 中滾珠的受力情況與（yǔ）雙（shuāng）螺母預緊結構中滾珠的受力情況（kuàng）類似(圖6)，而軸承3、4 的受力情況與軸承1、2 的受（shòu）力情況完全（quán）一樣，所以由靜力平（píng）衡條件可得

        2 p1nsinβ − p2nsinβ = Fx                        (20)

      式中 n ——單個軸承中（zhōng）的滾珠數（shù）

            β ——軸承中滾珠與滾道麵的接觸（chù）角（jiǎo）

       同樣（yàng）由（yóu）力學疊加原（yuán）理和（hé）赫茲（zī）接觸理論可得到

      當已知n、β、Fx 和p0 時，可（kě）由式(20)和式(21)求得p1 和p2 的值。

      得到了單個滾（gǔn）珠的法向接觸力後，由式(5)～ (16)可求得軸承外（wài）圈相對於軸承內圈的軸向位移量δB，最後由（yóu）式(4)求得軸（zhóu）承（chéng）的軸向剛度kB。

      在運（yùn）用（yòng）式(5)～(16)時，應將絲杠的結構參數用軸（zhóu）承內圈的結（jié）構（gòu）參數（shù）來替代，而將螺母的結構參數用軸承外圈的結構（gòu）參數來替代，由於不涉及到滾珠絲杠副中（zhōng）螺（luó）紋升角（jiǎo）φ 這（zhè）一概念（niàn），須（xū）將公式中（zhōng）的φ 值設為零值。

     通過以上的分析，分別得到了滾（gǔn）珠絲杠副中絲杠的軸向剛度kS，螺母組件（jiàn）的軸向剛度（dù）kN 和支（zhī）承軸（zhóu）承的軸向剛度kB，可方便地由式(1)求得整個滾珠絲杠副（fù）係統的軸向剛度kx。

      1.2 直線滾動導軌線（xiàn）剛度的計算

      一般數控機床上的直線滾動導軌副都是由兩滑軌和四滑塊組成，因此隻須（xū）計算單（dān）個滑塊的線剛度便可得到整個直線（xiàn）滾動導軌（guǐ）副的剛度。圖8為單個直線滾動導軌的結構示意圖及（jí）動力學模型圖。

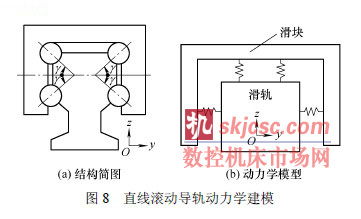
      以下分別計（jì）算單個直線（xiàn）滾動導軌的橫向(y 向)剛度和垂向(z 向)剛度。

      1.2.1 垂向剛度的計算

      如圖9 所示，當垂向力Fz 作用在滑塊（kuài）上時，各列中單個滾珠（zhū）的彈性力分別為F1、F2、F3 和（hé）F4，其中F1= F2 ，F3 =F4。γ 為（wéi）滾（gǔn）珠與滾道麵之間的（de）接觸角。

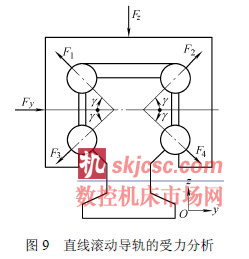
      由靜力平衡條件可以得到

2 (F1 − F3)  msinγ = Fz                (22)

      由力學疊加（jiā）原理和赫茲接觸理論可得到

      式中 m ——單列滾道的接觸滾珠數

            F0 ——由預壓載荷引起的單個滾珠的法向力（lì）

       當已知m、γ 、Fz 和F0 時，可由式(22)、(23)求得F1 和F3 的（de）值。已知單個滾珠所受法向力，參照圖5 所示的計算分析方法（fǎ），便可求得滾珠的變形（xíng）量，最後得到單個直線滾動軸承的垂向剛度kg，整個直線滾動導軌副由四個同樣的（de）導軌單元並聯組成，因此總的垂向剛度（dù）kz＝4kg。

      值得關注的是，由於直線滾動導軌的結構與（yǔ）滾珠絲杠、滾動軸承不同，滾珠與滾道麵接觸處的四個主曲率中，ρ22 的值應取（qǔ）零。

      1.2.2 橫向剛度的計算

      直線滾動導軌橫向(y 向)剛度的計算方法與垂向剛度的計算方法相同（tóng），不再贅述（shù）。

      通過以上分析計算，得（dé）到帶滾珠絲杠副的直線滾動導軌（guǐ）結合部空間三個相互垂直方向上的靜剛度，它們分別是滾珠絲杠（gàng）副的軸向（xiàng）剛度kx，直線滾動導軌副的橫向剛度ky 和垂向剛（gāng）度kz。這樣，便建立（lì）帶滾珠（zhū）絲杠副導軌（guǐ）結（jié）合部的動態特性參數模型（xíng）。

2 算例

      2.1 基本參數

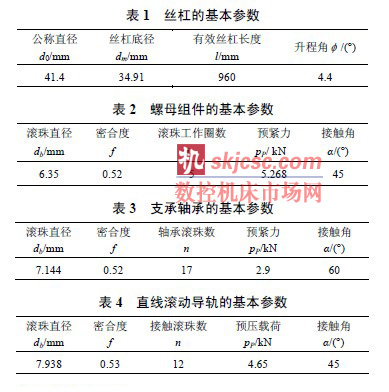
      本文（wén）以一款立式加工中心為例，將本文建立的帶滾珠絲杠副（fù）直線滾動導軌（guǐ）模型，應用於加（jiā）工中心動力學特（tè）性分析，驗證理論模型的有效性。表1～4列出了帶滾（gǔn）珠絲杠的直線滾動導軌副的幾何、物理參數。

      2.2 結果與討論

      2.2.1 工作載荷對剛度的影響

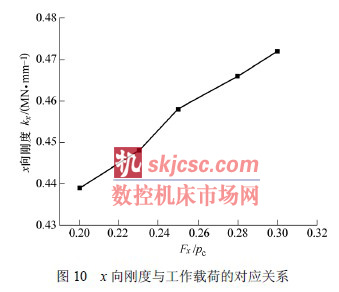
      為揭示工作載荷（hé）對結合部剛度（dù）特性參數的影（yǐng）響規律，作者運用本文提出的計算方法，分（fèn）析了結合部三個方向剛度與工作載荷的變化規律。圖10所示為結合部x 向剛度與其承受（shòu）載荷的關係曲線。

      查閱手（shǒu）冊，螺母組件的額定動載荷pc=52.7 kN，按照技術要求，工作載荷（hé）F 在（zài）0.2pc～0.3pc 範圍內變化。可以看出，結合（hé）部x 向（xiàng）剛度值隨（suí）著工作載荷的增大而略有（yǒu）上升，上升幅度在7%左右。

      由於直線滾動導（dǎo）軌（guǐ）滾珠與滾道（dào）麵的接觸角為45°，所以結合部z 向接觸剛度與工作載荷的（de）關係與y 向（xiàng）相等。

      以上分析揭示了工作載荷對結（jié）合部剛（gāng）度特性參數的（de）影（yǐng）響規律（lǜ），在工（gōng）作載荷允許的變化範圍內，剛度值的（de）變化量一般（bān）為10%左右。

      2.2.2 結合部動態參數應用

      本（běn）文研究的立式加工中心為x、y、z 三軸（zhóu）聯動機（jī）床，帶滾珠絲杠副的直線滾動導軌結（jié）合部，分別位於立柱和銑頭、床身和床鞍、床鞍和工作台之間 (圖12)。用彈簧單元模擬結合部接觸剛度，以靜止狀態(假定零工作載荷)為對象，經計算，可（kě）以得到此結合部x、y、z 三個方（fāng）向上的剛度值分別是：

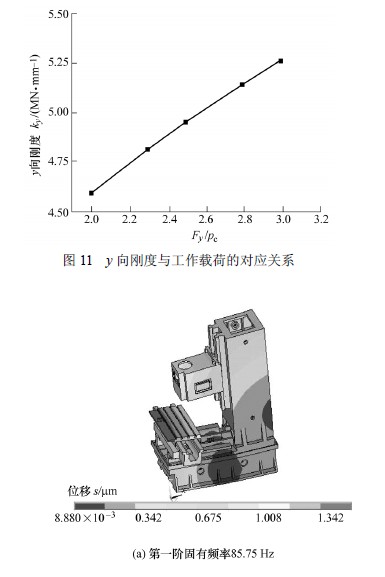
      kx=0.419 7 MN/mm，ky=3.512 MN/mm，kz=3.512MN/mm。基於ANSYS 軟件，分析機床整機固有頻率特性，得到前四階固有頻率分別為85.75 Hz， 102.15 Hz，137.33 Hz，145.44 Hz，其振型如圖13所示。

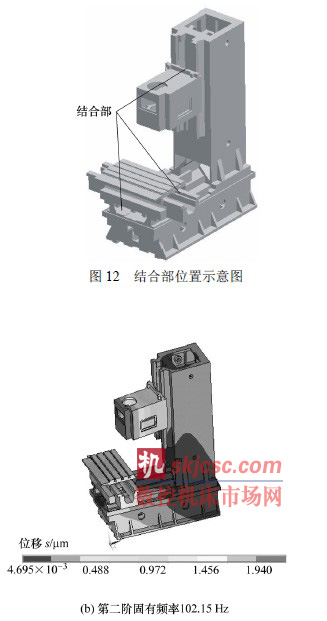
      表5 列出了結合部（bù）按照剛性連接簡化處理與運用本文理論模（mó）型的整機（jī）固有頻率特性比較（jiào）。

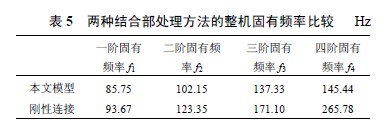
      可以看（kàn）出，結合部動態參（cān）數的描述是影響機床（chuáng）整（zhěng）機動力學性能的重要因素，特別是對於高階固有頻率特（tè）性計算，影（yǐng）響更（gèng）為明顯，因此（cǐ），研究帶（dài）滾珠絲杠副直線滾動導軌接觸剛度（dù）動態模型，對機床整機動（dòng）態特性分析與設（shè）計有（yǒu）重（chóng）要意義。

3 結論（lùn）

      (1) 運用赫茲接觸理論，分（fèn）析計算直線滾動導軌的線剛度、滾珠絲杠副（fù）和角接觸球軸承的軸向剛度，在此基礎（chǔ）上，建立了帶滾珠絲杠（gàng）副（fù）機床直線導軌（guǐ）結（jié）合（hé）部的動態剛度（dù）特性模型，開發了通（tōng）用計算（suàn）軟件。

      (2) 以一台立式加工中心為對象（xiàng），分析計算（suàn）了結合部三個方（fāng）向動態剛度隨工作載（zǎi）荷的（de）變化規律，揭（jiē）示了在工作（zuò）載荷變化範圍內，結合部動態剛度的變化值（zhí）一般小於10%。

      (3) 考慮帶滾珠絲杠副（fù）的（de）直線導軌結合部動態影響（xiǎng），分析計算了立式加工中心的整機動態特性，說明結合部動態參數是影響機床整（zhěng）機動力學性能的重要因素，特別是對於高階固有頻率影響更為明顯。研究表明：帶滾珠絲杠副（fù）的直線（xiàn）導軌結合部動態參數分析模型，具有物理概念清晰、計算簡單等特點。