基於切比雪夫多項式的數控機床幾（jǐ）何誤（wù）差參數化建模 -刨插拉床網-數控機床市（shì）場網

您現在的位置：刨插拉床網> 技術前沿>基（jī）於切比雪夫多項（xiàng）式（shì）的數控機床幾何誤差參數化建模

基於（yú）切比雪夫多項式的數控機床幾何誤差（chà）參數化建模

2017-12-29 來源：浙（zhè）江衢州廣播電視浙江大學（xué）機械工程作者：郭（guō）然付國強孫磊傅建中

摘要: 為了快速精確地建立機床幾（jǐ）何誤差項數學（xué）模型，提出了一種基於切比雪夫多項式的參數化建模方（fāng）法。首先針對測量得到的機床基本幾何（hé）項數（shù）據，將機床相應運動軸（zhóu）進給量轉化為切比雪夫變量。其次將切比雪夫變量代入不同階次的切比雪夫多項式得到相應的值。然後根據切（qiē）比雪夫基函數值和切比雪夫變量用多元線性回歸方法獲（huò）得相應的係數，得到關於切比雪夫基函數的數學模型。最後將運動軸進給量與（yǔ）切比雪夫變量（liàng）之間的轉化（huà）關係代入得到（dào）基本幾何誤（wù）差項的數學模型。建模過程簡單且易程序化，切比雪（xuě）夫（fū）多項式的高逼近精度使得建立的模型精度高。將所有幾何誤差項（xiàng）參（cān）數化（huà）模型（xíng）代入機床幾（jǐ）何誤差模型綜合數學模型，從而可得（dé）到機（jī）床工作空間幾何誤（wù）差場分布。以MV-5A 三軸立式加工中心（xīn）為例，將各個幾何誤差項參數化模型（xíng）代入機床幾何（hé）誤差模（mó）型中得到該機床綜合幾（jǐ）何誤差數（shù）學模型，進（jìn）而得到該機床工作空間（jiān）幾何誤差場分布，為機床設計和誤差補償（cháng）提供了理（lǐ）論依據。

關鍵詞: 數控（kòng）機床（chuáng）幾何誤差參數化建（jiàn）模切比雪（xuě）夫多項式

引言（yán）

隨著（zhe）製造業的快速發展以及工件精度（dù）要（yào）求和複雜度（dù）的提高，對機床精度的要求越來（lái）越高。機床幾何誤差和熱誤差是影響機床加工精度的主要因素，占60%以（yǐ）上［1 － 2］。而幾何誤差的建模和（hé）補償是提高機床精度的一種重要途徑。數控機床幾何誤差建模大多是基於多體理論建立齊次變換矩陣得到機床幾何（hé）誤差［3 － 6］。同時坐標係之間的微分變換關係和指數積理論也分別被用來進行誤差建模和補償［7 － 9］。根據模型進行補償的前提是數（shù）控機床基本幾何誤差項數（shù）據。三軸數控機床的21 項幾何誤差可通（tōng）過激光幹涉儀、球杆儀、激光跟蹤儀等裝置采用相應的測量方法得（dé）到。得到的誤差項數據是離散數據，反映（yìng）了機床行程一係列點的誤（wù）差，這就（jiù）需要建立機床基本誤差項的參數化模型（xíng），即建（jiàn）立相應的數學（xué）表達式。很多學者采用了（le）不同的方法來建立基本誤差項（xiàng）的模型［10 － 11］。Fan 等［12］引入正交多項（xiàng）式回歸法根據測量得到的誤差數據建（jiàn）立機床主軸熱誤差模型，又（yòu）采用正交多項式回歸法建立機床幾何誤差項數（shù）學模型［13］。Lee 等根據幾何誤差項的性質建立了合理的多項式模型，然後進行誤差測量（liàng）辨（biàn）識得到相應的係數［14］。

切比雪（xuě）夫多項式在函數逼近方麵比泰勒（lè）展開式有更高的精度。切比雪夫多項式已（yǐ）經在（zài）數字信號處理、衛星軌道、氣（qì）象學（xué）中得到廣泛應用［15］。相比於（yú）最小二乘法多項式擬合，隨（suí）著擬合次數的增加，切比雪（xuě）夫多項式各部分誤差減小（xiǎo），精度增加（jiā）［16］。本文提出一種基（jī）於（yú）切比雪夫多（duō）項式的機床幾何（hé）誤差項參數化建模方法。首先根據辨識得到的數據，結（jié）合幾何切比（bǐ）雪夫多項式性質，將機床位移變量進行變換。然後計算得到（dào）各個（gè）不同次數（shù）的切比（bǐ）雪夫多項（xiàng）式基函數的係數，接著代入機床位移變量轉換關係展（zhǎn）開得到相應（yīng）的幾（jǐ）何（hé）誤差項參數化模型。將幾何誤差項參數化模型代入機床綜合幾何誤差模型得到相應數學模型，從而可計算得到機床誤差場分布（bù），為機床（chuáng）設（shè）計和補償奠定基礎。

1、數控機床幾何（hé）誤差建（jiàn）模

三軸數控機床有21 項幾何誤差項。因（yīn）為（wéi）每個物體在空間上存在6 個自由度，所以每個運動軸存在6 項基本誤差項，包括3 項線性誤差和3 項轉角誤（wù）差。圖1 表示了X 軸的6 項基本誤差項。其中（zhōng）δxx、δyx、δzx分別是X、Y、Z 方向的（de）線性誤差，εxx、εyx、εzx分別表示繞（rào）X、Y、Z 軸的轉角誤差。同時由於安裝製造等原因，各個運動軸之間很難保證絕對的垂直，所以運動軸（zhóu）之間存在垂直度誤差。其中X 軸和Y 軸之間的垂（chuí）直度（dù）誤差為Sxy，X 軸和Z 軸之間的垂直度（dù）誤差為Sxz，而Y 軸和Z 軸之間的（de）垂直度誤差為Syz。那麽三軸數控機床存在18 項幾何（hé）誤差和3 項垂直度誤差。

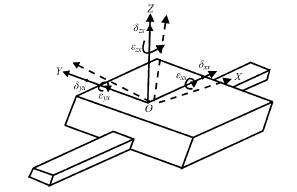
圖1 X 軸6 項基本誤差項（xiàng）示意圖

幾何誤差建模是（shì）誤（wù）差補償的基礎（chǔ）。本文以三軸立式加工中心MV-5A 為例（lì），為XYFZ 型（xíng）機床。圖2 所（suǒ）示為XYFZ 型（xíng）機床結構簡圖。該三軸數控機床可視為一個開環運動鏈，該運動鏈為工作台—X 軸—Y 軸—床身—Z 軸—刀具。可以采用指數積理（lǐ）論（lùn）對機床進（jìn）行幾何誤（wù）差建模，那麽機床刀（dāo）具相對於工作台的位置誤差可（kě）表（biǎo）示為

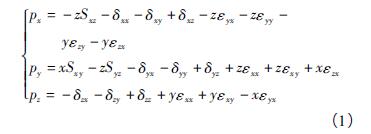
其中（zhōng）x、y、z 分別表示X、Y、Z 軸的位移，px、py、pz分別表示刀具在X、Y、Z 方向上的位置誤差。為（wéi）了能夠方便補償或者得到機床整個工作空間的誤差場分（fèn）布，機（jī）床誤差模型應該用數學表達式來表示（shì），這樣（yàng）機床工作空間內（nèi）任意位置處誤差都可得到。而各個誤差項的參數化建模是基礎，首先應建立誤差項相應的數學表達式模型。

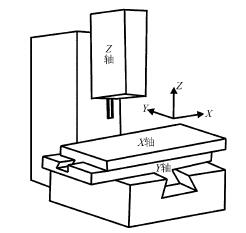
圖2 XYFZ 型機（jī）床結構簡圖

2 、幾何誤差項參數化建模

三軸數控機床的21 項幾（jǐ）何（hé）誤差中，垂（chuí）直度誤差（chà）與機（jī）床（chuáng）運動軸位移（yí）無關，是恒定值。而運動（dòng）軸基本誤差項會隨著軸進給量的變化（huà）而變化，同時隻與軸本身位移有關，與其他軸無關，則（zé）運動軸基本誤差項（xiàng）可表示為關於其位移的數學表（biǎo）達式。將各個誤差（chà）數學模型代（dài）入機床綜合幾何誤差模型（xíng）就能夠得到機床綜合幾何誤差的數學表達式。MV-5A 三軸立式加工（gōng）中心幾何誤差項可用激光幹涉儀采用9 線法辨識得到。下（xià）麵根據辨（biàn）識得到的MV-5A 機（jī）床幾何誤差項數據，采用切比雪夫多項式對幾（jǐ）何誤差進行參數建模。

2. 1 切比雪夫多（duō）項式

切比（bǐ）雪夫（fū）多項式是以遞歸方式定義的一係列（liè）正交多項式。第1 類切比雪夫多項式的根（gēn）用於多項式插值時可最大限度的降低龍格現象，可實現（xiàn）連續函數的最佳逼近。則第1 類切比雪夫（fū）多項式可由以（yǐ）下遞推關係得到（dào），即

數。基於切（qiē）比雪夫多項式進行（háng）擬合時，需要將變量（liàng）定義域轉換為［－ 1，1］，來確保切比雪夫（fū）多項（xiàng）式的精確性。切比雪夫多項式可用到幾何誤差項的參數化建模中（zhōng）。

2. 2 參數化建模步驟

MV-5A 三軸數控機床X 軸基本誤差項見表1。以X 軸x 方向的線（xiàn）性（xìng）誤差δxx為例進行基於切比（bǐ）雪夫多項（xiàng）式的參數化建模。

( 1) 機床X 軸行程（chéng）為600 mm，應轉換到切比雪夫多項（xiàng）式定義域［－ 1，1］內，則需要對其進行線性歸一化，相（xiàng）應的變量轉換關（guān）係為

( 2) 構建不同次數的（de）切比（bǐ）雪夫多項式基函數，並計算每個測量位置處對應的不（bú）同（tóng）次數的切比雪夫值。表2 所示為不同項的切比雪夫基函數值。前5 項切（qiē）比（bǐ）雪夫多項（xiàng）式可表示為

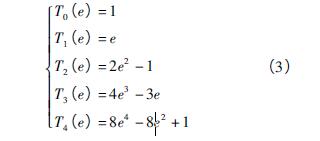
表（biǎo）1 X 軸6 項幾何誤差數據

表2 不同次數的切比雪夫基函數（shù）值

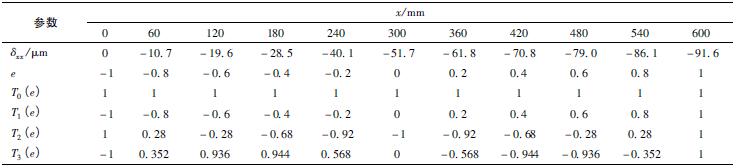
( 3) 計算切比雪夫多項式基函數對應的回歸係數。幾何誤（wù）差項的切比（bǐ）雪夫多項式模型可表示為

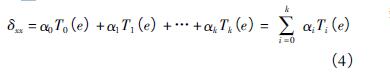
其中αi是切比雪夫多項式回歸係數。采用最小二乘法進行曲線擬合得到回歸係（xì）數，回歸（guī）係（xì）數與誤差數據之間的關係可表示為（wéi）

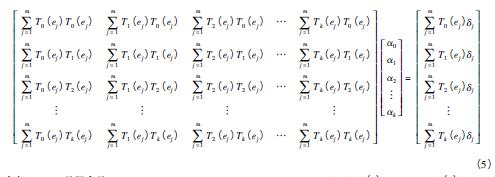
A 和B 矩陣（zhèn）可（kě）根據式( 5) 中相應的表達式代入測量數據計算獲得，從而計算得到切比雪夫多項式回歸係數。這（zhè）裏對於（yú）表1 中的（de）δxx，m = 11，選擇3 階切比（bǐ）雪夫多項式進（jìn）行擬（nǐ）合，即k = 3 進行計算（suàn），則式( 5) 表示為

得到的關於切比雪夫多項式（shì）基函數（shù）的擬合多項式為

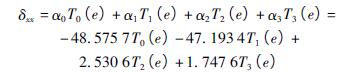
( 4) 將切比雪夫基函數代入基於切比雪（xuě）夫多項式的擬合函數中（zhōng）得到關於切比雪夫變量的多（duō）項式。即將式( 3) 代入到（dào）式( 4) 中可得到

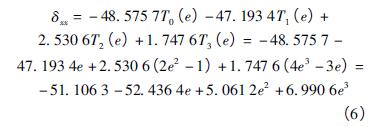
( 5) 根據（jù）變量轉換關係（xì）得到最終的基本誤差參數化模型和誤差曲（qǔ）線。即將式( 2) 代入到式( 6) 中得到基本誤差項（xiàng）關於運（yùn）動軸進給量（liàng）的多項式數學模型。δxx數學模型可（kě）表示為

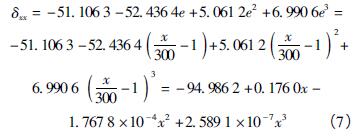
圖3 為（wéi）δxx誤差的切比雪夫多項式擬合曲線以及相應的殘差曲線。

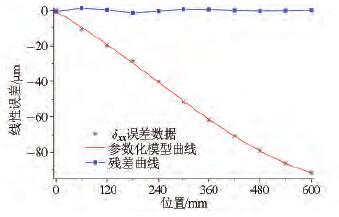
圖3 δxx誤差擬（nǐ）合曲線（xiàn）及相應的殘差曲線

基於切比雪夫多項式的幾（jǐ）何誤差參數化建模可以得到幾何誤（wù）差的數學模型。切比雪（xuě）夫多項式基函數（shù）將（jiāng）多項式擬合過程轉換為多元（yuán）線性回（huí）歸，這樣（yàng）使得計算簡單且易程序（xù）化。且（qiě）由於切比（bǐ）雪夫多項式的逼近精度（dù）高，建立的數學模型的精度和準（zhǔn）確性（xìng）大大提高。整個參數化建模過程可（kě）實現程序化，實現幾何誤差的（de）自動化建模（mó）。圖4 為基於切（qiē）比雪夫多項（xiàng）式的幾何誤差參（cān）數化（huà）建模流程圖。三軸數控機床（chuáng）18 項基本幾何誤差項按照此方法建立相應的參數化數學模型（xíng），然後將數學模型代入機（jī）床綜合幾何誤差模型中得到機床綜合（hé）幾何（hé）誤差的完整數學模型。

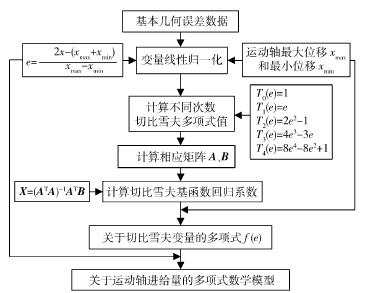
圖4 基於切比（bǐ）雪夫多項式的幾（jǐ）何誤差參數化建模流程圖

3 、實驗

采用美國光動公司的MCV-500 型激光幹涉儀測量MV-5A 三（sān）軸立式加工中心的幾何誤差項。由於MCV-500 型激光幹涉儀可（kě）以同（tóng）時測量定位誤差和直線度誤差，所以采用9 線法來測量幾（jǐ）何誤差。圖5 所示為激光幹涉儀（yí）測量機床幾何誤差。然後根據提出的基於切比雪夫多項式的幾何誤差參（cān）數化建模方法建立各（gè）個基本誤差項的數學模型。X、Y 和Z軸的基本（běn）幾何（hé）誤差數學模型為

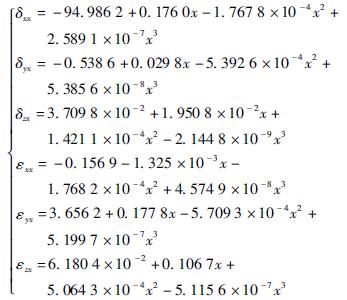
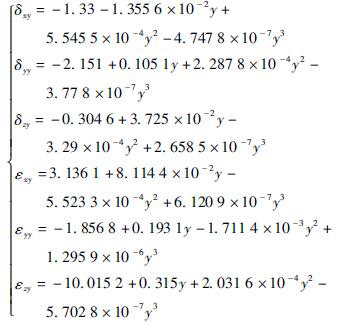
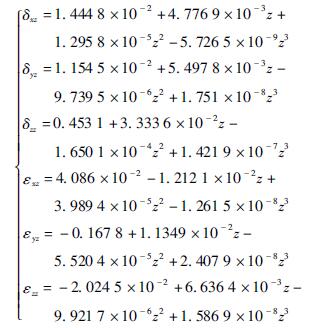
圖6 為X 軸基本誤差項數學（xué）模（mó）型曲線，包括3 項線性誤差和3 項轉角誤差。X 軸線性誤差的殘差為［－ 1. 269，1. 20］μm，轉角誤差（chà）數學模型的殘差（chà）範圍為［－ 1. 64，2. 29］μrad。圖7 表示Y 軸的基本誤差項數學模型曲線。圖8 表示Z 軸的基本誤差項數學模型曲線。建立的基（jī）本誤差參數化模型精度足夠高，可以（yǐ）很好地表示誤（wù）差數據。將基本（běn）誤差項模型代入式( 1) 得到MV-5A 三軸立式加工中心的幾何誤差（chà）數學模型為（wéi）

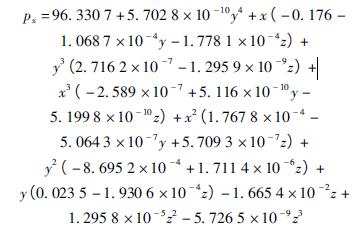
圖5 激光幹涉儀測量機床幾何誤差

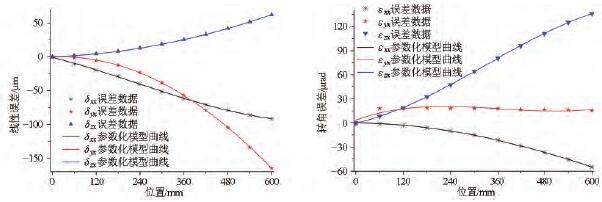
圖6 X 軸基本誤差項數學模型（xíng）曲線（xiàn）

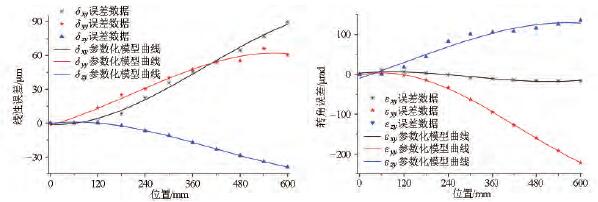
圖7 Y 軸基本誤差項數學模型曲線

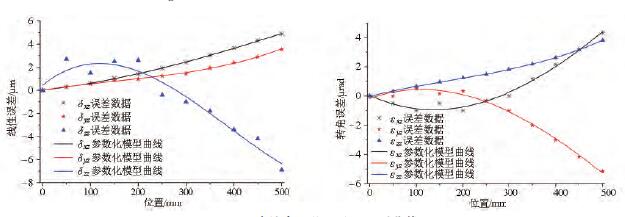
圖（tú）8 Z 軸基本誤差項數學模型曲線

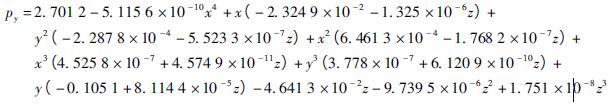
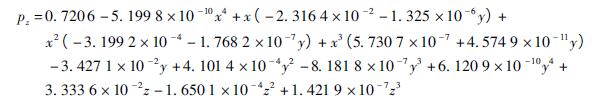
該模（mó）型即關於X、Y、Z 軸運動量的表達式。機床工（gōng）作空間上任意一點的幾何誤差都可以根據此數學模型計算得到。建立的綜（zōng）合誤差數學模型可以很好地預測機床的幾何誤差，可以得到機床的誤（wù）差場分布，機床幾何誤差場（chǎng）分（fèn）布可以為幾何誤差補償提供幫助，為後續補償奠（diàn）定（dìng）基礎。圖9 表示了在z =100 mm 處工作平（píng）麵上（shàng）的Z 方向上的幾何誤差（chà）以及綜合線性誤差分布。圖10 顯示了機（jī）床整個（gè）工作空間的誤差場分布。通過對誤（wù）差場分析可以（yǐ）得到機床部件安裝、製造對機床精度的影響，有利於提高機床（chuáng）精度。比如可分析得到機床導軌的（de）製造與安裝對機床的影響，從而對導軌進行調（diào）整來提高機床精度。誤差場分布也有助於機床的設計製造。

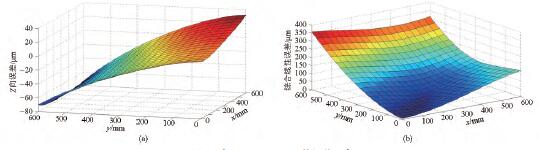
圖9 在z = 100 mm 平麵處（chù）誤差分布

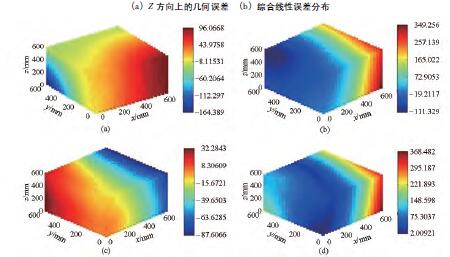
圖10 工作空間的幾何誤差場（chǎng）

4 、結束語

數控機床幾何誤差項參數化模型是（shì）建立機床幾何誤（wù）差數學模型和進行補償的基礎。本文運用切比雪（xuě）夫多項式提出了幾何（hé）誤差項參數化建模方法。切比雪夫多項式基函數將多項式擬合過程轉換為多元線性回歸，這樣使得計算簡單且易程序化。以MV-5A 三軸立式加工中心測量得到的δxx為例闡述參數化建模過程，首先根據幾何誤差項測量數據建立機床運動量和切比雪夫多項式變量之間的轉換關係。然後根據切比雪夫多項式基函數計算不同階次的切比雪夫多項式值。接著采用最小二乘法得（dé）到切比雪夫多（duō）項式基函數的（de）係數，從而得到關於切比雪夫變量的多項式模型。最（zuì）後代入機床運動量和切比雪夫（fū）342 農業（yè）機械（xiè）學報2 0 1 5 年變量轉換關係得到（dào）幾何誤差項參數化模（mó）型。機床18 項基本誤差項都可得到參數化模型，由於切比雪夫多項式的逼近精度高，建立的參數化模型的精度和準確性大大提高，且（qiě）整個參數化建模過程實現了程序化，從而（ér）實現了幾何誤差（chà）的自動化建模。

投（tóu）稿箱：
如（rú）果您有機床行業、企業相關（guān）新聞稿件發表，或進行資訊（xùn）合作，歡迎（yíng）聯係本網（wǎng）編輯部（bù），郵箱（xiāng）：skjcsc@vip.sina.com

更多相關信息

名企（qǐ）推薦

業界（jiè）視點

| 更（gèng）多

行業數據

| 更多

博文選萃

| 更多