基（jī）於（yú）六維（wéi）力傳（chuán）感器的工業機器人末端負載受（shòu）力感（gǎn）知（zhī）研究（jiū）-機器人-數控機床市場網

您現在的位置：機器人（rén）> 技術前沿>基於六維力傳感（gǎn）器（qì）的工業機器人末端負載受力感知研究（jiū）

基於六維力傳感器（qì）的工業機器人末端（duān）負載受力感知研究

2018-8-24 來源：轉載作者：張立（lì）建胡瑞欽易旺民

摘要: 針對工（gōng）業機器人末端負（fù）載（zǎi）與外界環境接觸力的感知需求, 在機器人法蘭與負載之間設置六維力傳感器, 並研究一套標定與計算（suàn）方法, 綜合考慮（lǜ）負載重力作用、傳感器零點、機器（qì）人安裝傾角等因素, 利用不少於 3 個機器人姿態下的力傳感器數據, 可（kě）求得傳感器零點、機器人安裝傾角、負載重力（lì）大小、負載重心坐標等（děng）參數, 進一步可消除（chú）傳感器零點（diǎn）及負載（zǎi）重力對受力感知的影響, 精確得到機器人末端負載所（suǒ）受的外部作用力與力矩. 實驗得到對於重量從 320 N 到 1 917 N 的負載, 在靜態條件下, 感知外力的誤差在（zài）負載重（chóng）力的 0.28 % 以內, 感知外力矩的誤差在負載對傳感器（qì）力矩的（de） 0.59 % 以內.

關鍵詞 : 受力感知, 重（chóng）力補償, 零點標定, 六維力傳感器, 工業機（jī）器人

引用格式張立建, 胡（hú）瑞欽, 易旺（wàng）民. 基（jī）於六維力傳感器的工業機器人末端負載受力（lì）感知研究. 自（zì）動化學報, 2017, 43(3):439−447

在加工、裝（zhuāng）配等工（gōng）業機器（qì）人（rén）的應用（yòng）中, 機器人末端工具或工件與外（wài）界環境的接（jiē）觸力需要被精確地感知, 控製係統據此修正機器人的運動, 才能保證作業的柔順性. 在醫用（yòng）手術機器人的操作中, 也需要實時精確反饋手術工具與（yǔ）外界的接觸力, 保證手術過程的安全. 對機器人末端（duān）負載受力的精確感知是進行機器人柔順控製與安全保障的（de）基礎.在現有應用中, 通常在工業機器人（rén）腕部與末（mò）端負載之間安裝（zhuāng）六維力傳感器（qì）, 用於機器（qì）人的力反饋控製[2−5]. 六維力傳感器能夠測量空間任意力係中的三維正交（jiāo）力 (Fx, Fy, Fz) 和三維正交力矩 (Mx,My, Mz)[6]. 在靜態（tài）條件下, 機器人腕部六維（wéi）力傳感器測得的力與力矩數據由三部分組成（chéng）, 即: 1) 傳感器自身（shēn）係統誤（wù）差; 2) 負載重力作用; 3) 負載所受外部接觸力. 若要（yào）得到負載所受外部接觸（chù）力, 需要消除傳（chuán）感器係統誤差、負載（zǎi）重力作用兩方麵的影響. 對於機（jī）器人運動帶來的慣性力, 本文暫不（bú）考慮, 實際在機器人慢速運動中, 慣性力的影響可忽略.

傳感器自身係（xì）統誤差方麵（miàn）, 六維力傳感器在空載狀態下的讀數（shù）並不為零, 本文假定傳感器自身的係（xì）統誤差為常數, 並稱（chēng）之作 “零點”. 六維力傳感器在（zài）安裝負載（zǎi）後, 負載與傳感器間的緊固安裝方式及緊固程度也會對（duì）傳感器零（líng）點造（zào）成影響, 因此（cǐ）傳感器零點無法在傳感器空載時準確得到, 對於零點（diǎn）的測定必須（xū）在負（fù）載安裝的條件下進（jìn）行.負載重力影響方麵, 在機器（qì）人運（yùn）動過程中, 負載姿態隨之改變, 而重力方（fāng）向始終豎直向下, 因此負載重力對六維（wéi）力傳感器（qì）數據（jù）的（de）影響隨機（jī）器人的運動不斷變化（huà）, 對於負載重力影響（xiǎng）的消除需要根據當前機（jī）器人姿態實（shí）時進（jìn）行.

在（zài）傳感器零點的補償方麵, 文獻 [8 – 10] 調整機器人（rén）至一係列特定姿態, 部（bù）分姿態中重力對（duì）傳（chuán）感器某一測量（liàng）分量的作用可相互抵消, 進而綜合對應姿態的傳感器數據可消除重力影響, 求得傳感（gǎn）器（qì）零點.在負載重（chóng）力補（bǔ）償方麵, 文獻 [2, 4, 11 – 14] 采用（yòng）已知重量與重心位（wèi）置的負載, 根據機器人姿態實時計算（suàn）重力（lì）的影響, 消除了重力（lì）對六（liù）維（wéi）力傳感器力與力矩值的影響. 一（yī）般情（qíng）況下負載（zǎi）的重量（liàng）、重心位置並不已知, 需要在線測定. 文獻 [15 – 19] 默認機器人基座標（biāo）係 Z 軸與重（chóng）力方向相（xiàng）同（tóng）, 進而調整機器人使力傳感器到達特定姿態, 直接得到負載重力（lì）大小,並通（tōng）過變化機器人（rén）姿態標定傳感器的（de）安裝（zhuāng）角度, 文獻 [19] 進一步按照（zhào）力與力矩關係（xì）解得負載重心位置, 以此換算（suàn）消除（chú）負載（zǎi）重力對傳感器力（lì）矩（jǔ）測量的影響. 文獻 [8] 利用傳感器數據及力與力矩的關係, 采用最小（xiǎo）二（èr）乘法求解負載重力大小（xiǎo）及重心位置. 上述文獻 [2, 4, 8, 11 – 19] 均默認機器人基（jī）座標（biāo）係（xì） Z 軸與重力方（fāng）向相同, 但實際中工業機器人的（de）安裝並不針對重力方（fāng）向進行特殊設置, 機器人基座標係 Z 軸與重力（lì）方向往往（wǎng）存在偏角, 上述文獻中的重力補償（cháng）算法未考慮此方麵的誤差. 文獻 [5] 在重力補償中考慮了機器人的安裝姿態, 采用最小二乘（chéng）法求得了機器人安裝傾角、負載重力大小及重心坐標（biāo）, 對於重量為24.5 N 的負載, 消除負（fù）載重力作用後, 感知外力的最大誤差小於 1 N, 但文獻（xiàn） [5] 沒有考慮傳感器的零點問題.

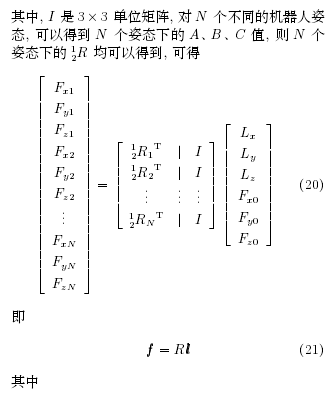
綜上所述, 已有對工業機器人腕部力傳感器負載受力感知的研究中, 傳感器安裝角度通（tōng）過標定計算得到, 傳感器零點通過調整機器人（rén）至一係列特殊姿態進行（háng）測定, 而機器人安裝傾角、負載重力大小及重心坐標則利用不同姿態下的傳感器（qì）數（shù）據通過（guò）最小二乘（chéng）法求得.

本文研究一種工業機器人腕部力傳感器負載（zǎi）受力感知方法, 與已有方法不同, 本文方法在通過機械定位保證傳感器安裝角度的基礎上, 利用不少於（yú） 3個機器人一般姿態下的傳感（gǎn）器數據, 采（cǎi）用最小二乘法一次求得傳感（gǎn）器零點、機器人安裝傾角、負載重力大小、負載（zǎi）重心坐標等參數, 進而（ér）消除傳感器（qì）零點及負載重力對受力（lì）感知的影響, 精確得（dé）到（dào）機器人末端負（fù）載（zǎi）所受的外部力與力矩數據.

1 、計算模型建立

1.1 六維力（lì）傳感器力與力矩的關係

將六維力傳感器（qì）三個力分量的零點值記為

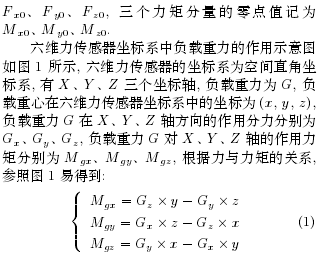
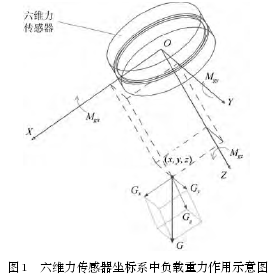
式 (28) 和式 (29) 即（jí）完成了對傳感器（qì）零點及負載重力影（yǐng）響的補償, 得到了負載所受的外（wài）部力與力矩.2 外力感知實驗2.1 實驗條（tiáo）件實驗采用 KUKA 公司的（de） KR210 機器人, 其主（zhǔ）要參數見表 1. 六維力傳感器采用 ATI 公（gōng）司的Omega190 型傳感器, 其測量範圍及（jí）精度參數（shù）見表2.

表（biǎo） 1 KR210 機（jī）器人性能參（cān）數（shù）

表 2 Omega190 技術參數

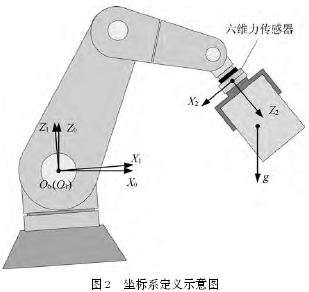
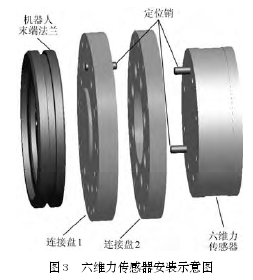
六維力傳感器（qì）在機器人末端法蘭的安裝方式如圖（tú） 3 所示, 傳感器自身的 2 個定位銷孔（kǒng）通過兩個定位銷與連接盤 2 實現定位, 連接盤 2 的中心圓孔通過連接盤 1 兩（liǎng）側中心的圓（yuán）形凸台與機器（qì）人法蘭中心的圓形凹腔（qiāng）實（shí）現中心定（dìng）位, 連接盤 2 又通過穿（chuān）過連接（jiē）盤 1 的定位銷與機器人法蘭銷孔實現（xiàn）方向定位.這（zhè）樣, 連接盤 1、2 兩（liǎng）側安裝麵的平行度保（bǎo）證了傳感器安裝麵與機（jī）器人法蘭安裝麵的平（píng）行, 確（què）保（bǎo）傳感器（qì）Z 軸與機器人工具坐標係 Z 軸的平行, 連接盤 1、2的中心定位及 3 個定位銷的輔助定位, 確保了（le）傳感器 X/Y 軸與機（jī）器人工（gōng）具坐標係 X/Y 軸的平行.

試驗中六維力傳感器負載采（cǎi）用如圖 4 所示的配重（chóng）塊, 共（gòng）采用 7 個配重塊, 每塊重約 27 kg, 首個配重塊通過連接法蘭與傳感器連接（jiē）, 後續配重塊之間可通（tōng）過（guò）連接孔逐個累（lèi）加或拆下, 在試驗中實現負載重量的調整. 實（shí）驗用係（xì）統的實物照片如圖 5 所示.

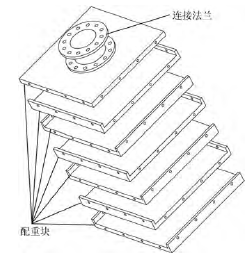
圖 4 試驗用配重塊示意圖

圖 5 係統（tǒng）實物照（zhào）片

2.2 實驗過程及（jí）結果

為充（chōng）分驗證所研究（jiū）的算法, 分別對 7 種負載重量 (安裝 1 ∼ 7 個配重塊) 下（xià）的（de）重力補（bǔ）償精度進行實驗驗證.對每種負載, 調整機器人到表 3 所列的（de） 8個姿態采（cǎi）集傳感器數（shù）據. 試驗中（zhōng）傳感器采（cǎi）樣（yàng）頻率為（wéi）7 000 Hz, 連續采集 500 個求平均作為計算（suàn）參考數據. 給出安（ān）裝 7 個配（pèi）重塊時采集的傳（chuán）感器數據見表（biǎo）4.計算（suàn）得到 7 種負載情（qíng）況下的負載重力、機器人安裝傾角參數如表 5, 7 種（zhǒng）負載情況下得到的傳感器零點如表（biǎo） 6, 而後調整機器人至 (A: 0◦, B: 90◦, C:0◦) 的（de）姿態, 進行外力感知計算, 在負（fù）載不受外（wài）力的條（tiáo）件下, 記錄消除（chú）傳感器零點及負載重力影響後的數據作為（wéi）補償誤差（chà）, 誤差統計結（jié）果見（jiàn）表 7, 其（qí）中, Fe為重（chóng）力補償後傳感器 3 個力分量的合力大小, Me為重（chóng）力補償後傳感器 3 個力矩分量的（de）合力矩大小, G為（wéi）測得的負載重力大（dà）小, Mg為機器人姿態 (A: 0◦,B: 90◦, C: 0◦) 時負載對傳感器的力矩大小, 此時傳（chuán）感器（qì） Z 軸近似與水平麵平行, 負載對傳感器的力矩可由（yóu） Mg= G × z 估算得到. δF表示 Fe相（xiàng）對於G 的（de）百分比, δM表示 Me相對於 Mg的百分比.由（yóu）表 7 可見, 消（xiāo）除傳感器零點及（jí）負載重力作用後, 感知外力誤差在負載重力的 0.28 % 以內, 感知外力矩的誤差在負載對（duì）傳感器（qì）力矩的 0.59 % 以內

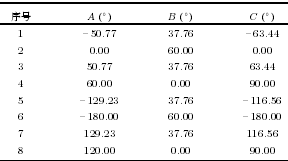
表 3 機器人姿態列表

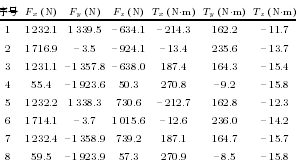
表 4 加載 7 個配重塊（kuài）時的傳感器數據

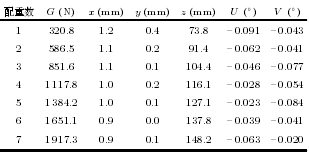
表 5 負載重力及機器人（rén）安裝傾角計算結果

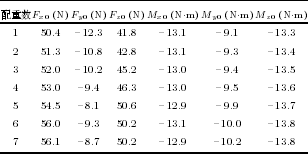
表（biǎo） 6 六維（wéi）力傳感器零（líng）點計算結果

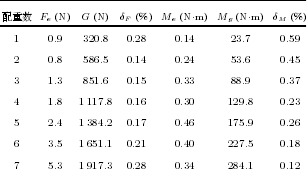
表 7 受力感知誤差統計

為驗證采用（yòng）所述方法測量負載重力的精度, 通過其他測量方（fāng）式實（shí）測所安（ān）裝負載的重量進行對（duì）比.表 5 中得到的負載重力包含了（le）安裝（zhuāng）至六維力傳感器上所有零部件（jiàn）的重量, 同時也包含（hán）了六維力傳感器敏（mǐn）感端自身的重量. 而傳感器敏感端無法拆下單獨稱（chēng）重, 因此, 在六維力傳感（gǎn）器空載（zǎi）情況下 (即（jí）不安裝任何零部件至傳感器), 進行與上（shàng）述（shù）完全（quán）相同的（de）實驗過程, 計算（suàn）得到傳感器敏感端自重為（wéi） 35.5 N.表 5 中負載重力 G 減去傳感器敏感端重（chóng）量, 即可得（dé）到安裝至傳感器上零部件的重量, 如表 8 “安裝重量計算值（zhí）” 所示. 另一方麵, 實（shí）測安裝至傳感器上零部件的重量. 使用 S 型拉力（lì）傳感器, 采用（yòng）懸掛方式測（cè）量（liàng）, 選用中諾（nuò）傳感器公司（sī） ZNLBS-200 型傳感器, 量（liàng）程（chéng） 200 kg, 測量精度0.05 %, 即 200 × 0.05 % = 0.1 kg, 傳感器示數乘重力常數 g = 9.8 m/s2, 得到表 8 中 “安裝（zhuāng）重量實測值”. 表 8 顯示, 負載重力測量的最大誤差為 1.2 N,接近於拉力傳感器的（de）測量誤差.

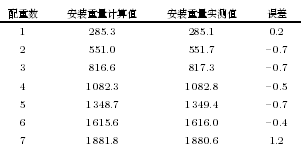
表 8 負載重力測量誤差統計 (N)

3、感知誤（wù）差分析

3.1 傳感器（qì）測量（liàng）精度的影響

表 2 給出了所用六維（wéi）力傳感器的測量精（jīng）度, 數據來自原廠給出的精度測試報告, 列出的精度指標為測試（shì）中出現的全量程最大精度偏差. 其中, 力最大偏（piān）差為 18 000 × 0.09 % = 16.2 N, 力矩最大偏差為 1 400 × 0.87 % = 12.18 N·m. 實驗中對連續采集的 500 組傳感器求平均作為（wéi）參考數據, 因此, 傳感器誤差的影響達不到上述最大偏差數值. 對采集的傳感器數據求平均一定程度減（jiǎn）小了數據的隨機波動,但不能完全消除, 波動的程度會造成最終的感知誤差. 為評估求平均後數據的（de）波動程度, 在靜止狀態下, 連續采集傳感（gǎn）器數據序列 65 000 組, 每 500 組求平均後得到 130 組（zǔ）數據. 對於求平均得（dé）到的數據序列, 對 6 個測量分量, 求出每個分量（liàng）數據序列（liè）中最大值與最（zuì）小值的差（chà） D 及標準差 σ, 以評價數據的波（bō）動程度, 見表（biǎo） 9.

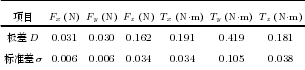
表 9 參考（kǎo）數據隨機誤差

對於力的感知誤（wù）差, 表 9 中的波動值遠小於表 7中的誤差值 Fe. 對於力矩, 表 9 中的波（bō）動值則與表7 中的誤差值 Me相當. 因此, 對於表 7 中的感知誤差, 力矩感知誤差可以通過數據隨機誤差解釋, 而（ér）力感知誤差則存在其他原因.

3.2 機器人姿態角度誤（wù）差（chà）的影響

本文在計算中直接使用了機器（qì）人控製係統提供的 A、B、C 值, 即機器人工具坐標係相對於基座標係的角（jiǎo）度值. 控製係統給出的角度值與真實（shí）值間（jiān）的誤差將（jiāng）對最終的受力感（gǎn）知帶來誤差.按照所述算法, 仿真計算所述角度誤差對（duì）最終受（shòu）力感（gǎn）知的影（yǐng）響, 仿真所采用的機器人姿態讀數與表 3 實驗數據（jù）完全（quán）相同, 所用負載質量特（tè）性（xìng）及機器人底座傾角（jiǎo）數（shù）據采用表 5 中第（dì） 7 行的數據. A、B、C值（zhí）的誤差為人為指定（dìng）, 得出不同 A、B、C 誤差引起的機器人在姿態 (A: 0◦, B: 90◦, C: 0◦) 下的受力感知誤差如圖 6 所示.

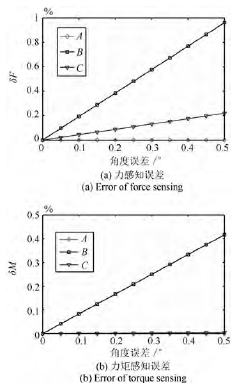
圖 6 機器人姿態誤差對受力感知的影響曲線

圖 6 中的 3 條曲線對應 A、B、C 值各自誤差對受力感知的影響. 由圖 6 可見, 受力感知誤差與角度誤差近似呈正比（bǐ）例線（xiàn）性關係, 機器人在姿態 (A: 0◦,B: 90◦, C: 0◦) 時（shí）, B 值誤差的影響遠大於 A、C,因此, 下麵分析 B 值誤差引起受力感知誤差的具體大小（xiǎo）.對於工業（yè）機器（qì）人的絕對定位誤差, 機器人製造商（shāng）往往（wǎng）不給出相關數值, 而需要使用者自行測量標（biāo）定[20−21]. 文（wén）獻 [22] 對（duì） KUKA公（gōng）司 KR500 機器人(額定負載（zǎi） 500 kg) 進（jìn）行了誤差測量, 機器人工具坐標係姿態角度誤差平均值為 0.21◦[22], 文獻 [23] 對ABB 公司的 IRB1 600 機器人進行誤差測量, 最大角度誤（wù）差（chà）為 0.16◦. 參照參考文獻中的測量結果, 假定 B 值誤（wù）差為 0.1◦, 仿真計算由此造成的實驗中 7種負（fù）載下的（de）受力感知誤差, 結果如表 10 所示.

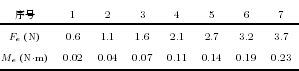
表 10 仿真受力感知誤差統計

對（duì）比表 7 與表 10, 對於力的感知誤差 Fe, 仿真結果與實驗吻合（hé）較好, 因此（cǐ）, 實驗（yàn）中力的感知誤差可（kě）以由機器人（rén）角度誤差解釋. 而對於力矩的感知誤差Me, 對比表 10 與表 9, 表 10 中的誤差值被數據隨機誤差“淹沒（méi）”.上述的實驗與仿真計算可以表明, 表 7 中力的感知誤差主要由（yóu）機器人（rén）姿態（tài）角度誤差引起, 力（lì）矩感知誤差（chà）主要由采樣數據的隨機誤差引起（qǐ）.

4、結論

本（běn）文麵向工業機器人在加工、裝配等應用中（zhōng）精確測量（liàng）外力的需求, 在機（jī）器人末端（duān）與負載之間設置六維力傳感器, 並研究一套標定與計算方法, 在（zài）通過機械定位（wèi）保證六（liù）維力傳感器與機（jī）器人安裝精度的條（tiáo）件下, 方法（fǎ）綜合考慮了負載重力作用、傳（chuán）感器零點、機器人安裝傾角等因素, 利用不少於 3 個機（jī）器人姿態下的力傳感器數據, 采用最小二乘法求得傳感器零點、機器人安裝傾角、負載重力大小、負（fù）載重心坐（zuò）標等參數, 進一步消除傳感器零點及負載重力（lì）對受力（lì）感知（zhī）的影響, 精確得到機器人末端負載（zǎi）所受（shòu）的外部（bù）作用力與力矩.實驗中（zhōng）對於（yú）重（chóng）量從 320 N 到 1 917 N 的負載,重力（lì）補償後傳感器感知外力的誤差在負載重力（lì）的（de）0.28 % 以內, 感知外力矩的（de）誤差在負載對傳感器（qì）力矩的 0.59 % 以內. 實驗與仿真計算表明, 力的感知（zhī）誤差主要由機（jī）器人姿態角度誤差引（yǐn）起, 力矩感知誤差主要由采樣數據（jù）的隨機誤差（chà）引起.相對已有方法, 本文方（fāng）法的優勢在於:

1) 應用過程得到簡化: 已有方法需要先調整機器人到（dào）一（yī）係列特定姿態進（jìn）行傳感器數據采集, 首（shǒu）先完成零點標定計算, 在消除零點的基（jī）礎上, 再調整（zhěng）機器人到一係列一般姿態進行傳感器數據采集, 計算得（dé）到負載重力影響參數, 前後需要 2 次機器（qì）人姿態調整及數據采集計算過（guò）程, 而本文方法隻需（xū） 1 次機器人姿態調整過程, 得到（dào）不少於 3 個機器人姿態（tài）下的傳感器數據, 即可計算得出全部所需參數. 另一方麵, 采用特殊姿態進行零點標定的過程中, 機器人（rén）運動幅度大,操作時間較長, 且（qiě）在空間有限的情況下難以操作, 而本文方法隻需機（jī）器人的（de）一係列一般姿態, 機器人運動幅度小、效率高, 在（zài）空間有限的情況下也可實施.

2) 有望提高感知精度: 相對於已有方法（fǎ）利用特定（dìng）機器（qì）人姿（zī）態下的傳感器數據, 本文（wén）方法中傳感器零點通過一般機器人姿態下的傳感器數據計算得到,計算結果更具一般（bān）性, 有望提高零點精度. 已有方法中傳感（gǎn）器零點通過獨立的過程求出, 沒有充分考慮零點與（yǔ）其他參數（shù）的耦合影響, 本（běn）文方法中所有參數聯立建模求解, 各參（cān）數間的耦合（hé）作用被充分考慮, 這也（yě）有（yǒu）助於提高結果精度. 另一方麵, 本文方法能夠在機器人最終的目（mù）標姿態附（fù）近進行姿態變換完（wán）成零點標定, 求得的（de）零點更接近傳感器在機器人目標姿態下的零點數值. 而已（yǐ）有采用特（tè）殊姿態進行零點標（biāo）定的方（fāng）法則很難有（yǒu）針對性地對特定姿態下傳感器的零（líng）點進行標定.

投稿箱：
如果您有機（jī）床行業、企業相關新聞稿件發（fā）表，或進行資訊合作，歡迎聯係本網編輯部，郵（yóu）箱：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視點

| 更多（duō）

行業數據

| 更多

博文選（xuǎn）萃

| 更多