摘　要：為了降低加工過（guò）程的熱誤差，提高數控機床加工（gōng）精度，基於（yú）時序相關分析理論與數值計算方法，建立了（le）一種以溫度（dù）場分布及加工參數為輸入的新型機床（chuáng）主軸熱（rè）誤差建模方法．所建（jiàn）模型由熱誤差模型、主軸動壓軸承熱特性模型以及主軸熱傳遞模型三部分組成．該方法首先根據時序相關理論建立熱（rè）誤差與溫度（dù）測點之間（jiān）的相關模型，再通過灰色相關理論完成關鍵溫（wēn）度測點位置與（yǔ）數量的優化，同時，基於數值計算與熱傳導理（lǐ）論，建立了動壓主軸係（xì）統熱特性模型（xíng）．以一台大型龍門（mén）導軌磨床為實驗對象，建立了磨床主軸箱熱誤差預測模型．實驗結果表明，所建立的熱誤（wù）差模型具有良好的熱誤（wù）差辨識性能．
   
        關鍵詞：時序相關分（fèn）析；雷諾方程；有限差分法；熱誤差
 
       機床熱誤差是精密加工誤差的主要來源之一，對其控製和補償是提高機床加工精度的（de）關鍵技術［１］．機（jī）床熱誤差補償涉及熱誤差檢測、熱誤差預測（cè）模型和熱誤差實時補償三類問題，其中熱誤差預測模型的建立最為關鍵［２］．
 
       機床熱誤差控製的最新技術是基於熱誤差預測模（mó）型的誤差實（shí）時補償技術（ＲＴＥＣ）［３］．由（yóu）於機床熱（rè）誤差可以看作是關於機床熱（rè）分（fèn）布、位（wèi）置以及運動方向的確定性函數［４］，故而，可以建立以機床溫度場分布和運動方向為自變量的熱誤差模型．同時，機床溫度場分布特性可以用若幹溫度測點處的數（shù）據來表征［５］．
 
      本（běn）文運用時間序列分析理論擬合熱誤差與相關溫度測點數據之間的關係（xì），采用數（shù）值計算方法建立某高精度磨床主軸熱特性模型，提高了此類熱誤差模型（xíng）的預測精度和（hé）魯（lǔ）棒性．
 
      １、　機床熱誤差模型的理論基礎
   
      １．１　時序分析建模方法
   
      時序分析是對觀測所得的有序隨機數據進行分析和處理的一種（zhǒng）方法，適用於輸入不可測或不確定測量數據（jù）的描述，常被用於機（jī）床熱誤差建模．
   
      根據時序（xù）分（fèn）析理論［６］，對一組測（cè）點進行第ｉ次測量的熱誤差χｉ可以分解為兩部分，如（rú）式（shì）（１）和式（shì）（２）所示，一部分是確定性部（bù）分，完全取決於各溫度測點處溫度序列Ｔｒ，ｉ的線性組合ｆ（ｉ）；另一部分是隨機性部分，完全獨立於Ｔｒ，ｉ ，由殘量εｉ確定（如儀（yí）器的測量誤差）．同時，假定（dìng）εｉ是零均值的獨（dú）立序列，即（jí）白噪聲序列，因而，對（duì）於不同ｉ值，εｉ是相互獨立的．
 

 
      采（cǎi）用一階自回歸模型描述殘差，如式（５）所（suǒ）示：
 

      綜（zōng）上所述，由一組測點確定的熱誤差（chà）計算模型如式（７）所示：

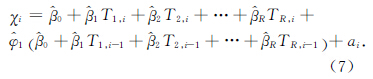
     １．２　機床（chuáng）溫度測點優化方（fāng）法
   
    機床各部（bù）分溫度的（de）分布特性是熱誤差產生的內在原因，因而，溫度測點數量和位置的選取（qǔ）將直接影響式（７）計算誤差的準確性．基於已（yǐ）有的測試數據，采用灰色關聯度分析（xī）方法進行溫度測點位置和數量的優（yōu）化選（xuǎn）取，可以將測點數目控製在合（hé）理（lǐ）範圍內（nèi）的同時，提高式（７）的計算精度．
 
    灰色關聯度分析是（shì）按照係統（tǒng）中各特征參（cān）量序列之（zhī）間（jiān）的相（xiàng）似程（chéng）度進行係統分析的一種方（fāng）法［７－８］，保證各特（tè）征（zhēng）參量間的等效性和同（tóng）序性，是進行（háng）關聯（lián）度分析的前提（tí）．
 
    采用極差變換法的一種改進形式，對（duì）熱誤差（chà）與各溫度測點的實測結果進行無量綱化處理，如式（８）所示：
  
    

     
  
     將各個比（bǐ）較序列（liè）對同一（yī）參考序（xù）列的關聯度按大小順序排列起來，即組成了（le）反映各個比較序列對同一參考序（xù）列的“主次”關係的關聯序．依據關聯序即可對磨床主軸各溫度測點位置分布及測點數（shù）量進行優化處理．
   
    １．３　動壓（yā）軸（zhóu）承的熱（rè）特性建（jiàn）模方法
   
    精（jīng）密磨床（chuáng）運行時，主軸軸承的摩（mó）擦熱是熱誤差的主要來源，通常也是主（zhǔ）要的溫度測點．在機（jī）床的實際運行中，高速旋轉和結構複雜的特點，難以用傳（chuán）感器（qì）對軸承處的溫度進行（háng）準（zhǔn）確測量．通（tōng）過建立主軸的熱特性描述模型，計（jì）算不同工況下主軸軸承處的溫度參數用於熱誤差建模，對於提高模型的精度和適（shì）用性都有主要（yào）意義．
 
    建立主軸動壓滑動軸承油膜（mó）熱特性計算模型的思路是通過對雷諾方程、溫粘方程等的聯立求解，得到動壓軸（zhóu）承達到平衡狀態時的平均溫度．計算流程如圖１所示．
 
    由於剛性徑向滑動（dòng）軸承的（de）油膜壓強分布滿足雷諾方程，基於相似理論，將坐（zuò）標原點（diǎn）置於軸承軸線上，且（qiě）位於軸承寬度的１／２處，對雷諾方程（chéng）進行無量綱化後得到［９］：
  
    

   
  
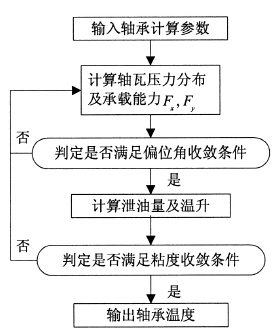
        圖１　主（zhǔ）軸動壓軸（zhóu）承熱特性計算流程圖
 
    式（１１）基於如下假設：
 
    １）潤滑油重（chóng）量及慣性力忽略不（bú）計；
    ２）油膜為牛頓流體（tǐ），且為層流；
    ３）潤滑油不（bú）可壓縮；
    ４）潤滑油為定常流體；
    ５）載荷（hé）方向為垂直於軸向．
    
    

     
  
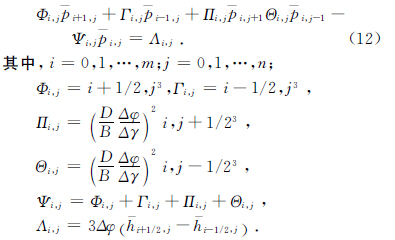
     求（qiú）解上（shàng）述方程（chéng）時，先確定承載區四周邊界的壓強，進（jìn）而求解整個求解區域上（shàng）的壓強分布．
 
    １．３．２　油膜偏位角的修正
 
    由於已知載荷方向，為了確保油膜壓力分布求（qiú）解的準（zhǔn）確性，需要進行油膜偏位（wèi）角的校核，從而保證油膜承載（zǎi）力的合力與載荷方向相反．  
  
   

    已知載荷方向為垂直於軸向，則軸承的偏位角應保證油（yóu）與膜合力方向相反，采用迭代法求（qiú）解穩定狀態（tài）下軸承的偏位角．修正方程為：
     
    
  
     １．３．３　溫粘方程的求解
      
    

    
    
     １．４　主軸熱傳遞模（mó）型
   
     已知主軸運轉過程中，動壓軸承油膜溫度如式（shì）（２１）所示，下麵討（tǎo）論求解主軸熱特性分布的（de）另一個關鍵條件（jiàn），即主軸熱傳遞模型．
 
      采用圓柱（zhù）坐標係描述主軸（zhóu）溫度分布，則不含內熱源的非穩態導熱微分方程（chéng）為

     
  
      其中，Ｔ 為溫度，ｒ 為半徑（jìng），ｚ 為軸向坐標，ｔ為時間，α為主軸散熱（rè）係數．
 
      式（２２）還基於如下假設：
 
     １）主軸材質均勻且各（gè）向同性；
     ２）主軸材料（liào）的特性係數（shù）為常數；
     ３）物體內無溫度躍變或物體相變；
     ４）主軸溫度不隨角度φ 的變化而變（biàn）化．
 
    采用分（fèn）離變量法，假定式（２２）有如（rú）下變量（liàng）分離形（xíng）式的解：
  
    

    
  
    ２　、熱誤差模型精度分析
   
    下麵以某高精度龍門導軌磨床主軸箱係統（如圖２所示）為研究對象，依據（jù）上述研究結果（guǒ）進行測試和建模，並對熱誤差模型精（jīng）度進（jìn）行分（fèn）析驗證．
   
    首先根據經驗（yàn）和（hé）初（chū）步分析確定１２個測試點（diǎn）：主（zhǔ）軸後端皮帶輪附近布置２個測點（１～２號測點）；主軸箱體上布（bù）置４個測點（３～６號（hào）測點）；主軸前（qián）段布置３個測點（diǎn）（７～９號測（cè）點）；電機上布（bù）置１個測點（１０號測點）；安裝（zhuāng）座上（shàng）布置２個測點（１１～１２號（hào）測點），如圖２所示．進行溫度測試采樣．測試條件為，磨頭主軸以１　０４０ｒ／ｍｉｎ和１　５００ｒ／ｍｉｎ的恒定轉速各空載（zǎi）運（yùn）行２．５ｈ，每間隔５ｍｉｎ用非接觸式紅外溫度測量儀（yí）測量１２個測（cè）點的（de）溫度各一次，與（yǔ）此同時，用千分表測量主軸在Ｘ，Ｙ，Ｚ 三個方向上對（duì）應的（de）熱漂移，總共獲取２組溫度和熱誤差數據（jù）．
 
     ２．１　主軸箱係統溫度測點（diǎn）優（yōu）化
   
     采用灰色關聯度分析法，將所測得的（de）主軸在Ｘ，Ｙ，Ｚ 三（sān）個（gè）方向上的熱誤差作為參（cān）考序列，所測得的１２組溫度測（cè）點數據作為比較序列．利用式（８）對各數據序列（liè）進行處理，通過式（９）和式（１０）求得各比較序列與參考（kǎo）序列間的灰關聯度，如圖３所示．
 
     經過關聯度大小的對比，排除關聯度小的溫度測點後，確定影響主（zhǔ）軸三個方向熱漂移的關鍵溫度（dù）測點總數由１２個（gè）降低為８個，分別是：１號、３號、４號、５號（hào）、６號、７號、１１號及１２號等８個溫度測點．其中，１號與７號測點位於主軸軸（zhóu）承處，需采用２．３節與２．４節建（jiàn）立（lì）的熱（rè）特性模型對該兩個測（cè）點處（chù）的溫度進（jìn）行預測．
 

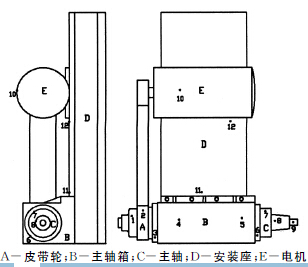
     圖２　龍門導軌磨床主軸箱係統溫度測點布置圖
   

    
    
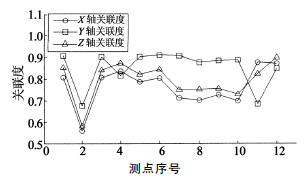
           圖３　熱誤差與（yǔ）溫（wēn）度測點間的關聯度
     
     ２．２　主軸熱特性建模與精度分析
   
     實（shí）驗（yàn）中所（suǒ）采用的磨床的主軸箱動壓軸承及其潤滑油的參數包括：寬徑比０．８，初始偏位角９０°，偏心率０．５，軸頸半徑０．１２０ｍ，軸（zhóu）瓦半徑（jìng）０．１６７ｍ，內切
圓半徑０．１２１ｍ，軸（zhóu）承張角１４７°，初始潤滑油動（dòng）力粘度０．０２Ｐａ·ｓ，初始潤滑（huá）油溫度２８℃，潤滑油比熱１　８８８Ｊ／（ｋｇ·℃），潤滑油密度８６７ｋｇ／ｍ３，軸承散熱（rè）係數８０Ｗ／ｍ２·℃，主軸轉速為（wéi）１　４７０ｒ／ｍｉｎ或１　５００ｒ／ｍｉｎ． 
   
    采用主軸熱特性模型和主軸熱傳遞模型，對１號與７號測點處溫度時間序列（liè）進行預測，同時，將預（yù）測值序列＾ｘｉ與兩個測（cè）點處的（de）溫度實測值序列ｘｉ進行對比，並（bìng）計算其相對誤差δ，結果如表１所示．相對誤差（chà）的計算公式如式（２７）所示：

      由表１可知：預測值序列與實測值序列的相對誤差較小，相對誤差（chà）平均值為１４．２％．其中，１號測點相對誤差（chà）最大值１３．３％，７號測點相對誤差３６．４％．因此（cǐ），主軸熱特（tè）性辨識（shí）模型（xíng）的預測數據與實測數據基（jī）本吻合，另（lìng）外考慮到（dào）１號和７號測點位（wèi）於主軸外露的軸頸處，測試所得溫度與軸承處的溫度本身存在一定的誤差，所以，本文建立的模型能有效地描述主軸的（de）熱特性．
   
     ２．３　熱（rè）誤（wù）差模型實驗驗證
   
     綜合主軸熱特性辨識數據和溫度（dù）測點數據，利用式（７）進行熱誤（wù）差模型的驗證．
 
     首先，基於第１組數據中各溫度測點數（shù）據序列和熱誤差數據序列，建立主軸Ｘ，Ｙ，Ｚ 三（sān）個方（fāng）向（xiàng）上的熱誤差預測模型．然後，選取（qǔ）未使用過的第２組數據中的溫度數據，代入熱誤差（chà）預測模型中，輸出Ｘ，Ｙ，Ｚ 方向的熱誤差預測值；最後，將預（yù）測值與熱誤差實測值比較．同時，預測過程中，第１號和７號測點的溫度數（shù）據采用主軸箱熱特性模型的輸出值．模型的熱（rè）誤差預測值與實測值，以及兩者之間的殘差如圖４，圖（tú）５和圖６所示．
  
  
                                表（biǎo）１　熱特性辨識（shí）結（jié）果

  
     
    
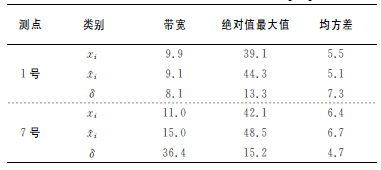
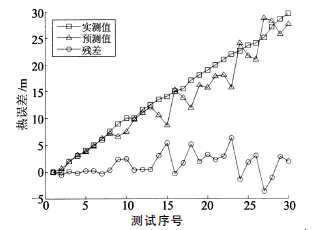
           圖４　主（zhǔ）軸Ｘ 方向熱漂移預測值與實測值比較
   

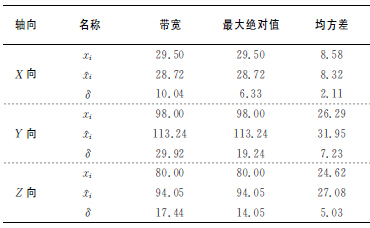
      如表２所示為本文（wén）所（suǒ）建立的熱誤差模型的性能指標．由表２可知，預測值序列＾ｘｉ與實測值序列ｘｉ的相對誤差δ較小，其中（zhōng），Ｘ 軸（zhóu）方向熱誤差相對誤（wù）差δ最大值６．３３％，Ｙ 軸方向（xiàng）熱誤差相對誤差δ最大值（zhí）１９．２４％，Ｚ軸方（fāng）向熱誤差相對誤差δ最大值１４．０５％．
 

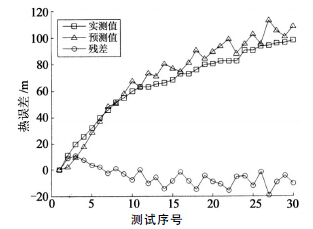
             圖５　主軸Ｙ 方向熱漂移預測值與實測（cè）值比較

  
        
  
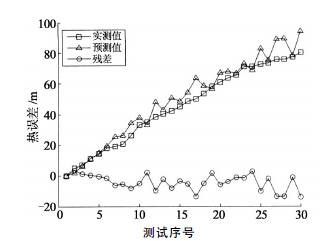
                圖６　主軸Ｚ 方向熱漂移預測值與實（shí）測值比較
 
 
                              表２　熱誤差辨識結果

     
  
  
      ３　、結　論
   
     １）基於空載實（shí）驗的精密導軌磨床熱誤差建模方（fāng）法，研究的（de）熱誤差不受其它加工因素的耦合影響，降（jiàng）低了熱誤差（chà）建模的複雜程度，對於切削力不（bú）大的精密磨（mó）削具有實用意義．
    
     ２）基於時（shí）序相關分析理論與數值計算理論的熱誤差模型（xíng）能有效地對機床熱（rè）誤差進行辨識．
   
     ３）實驗驗證了該建（jiàn）模方法的有效性與可（kě）行性，為機床精密加工精度的提高與熱誤差實時補償技（jì）術提供了理論借鑒．