數控車床圓弧麵螺紋車削研究與程（chéng）序開發-螺紋加工機床（chuáng）網-數控機床市場網

您現在的位置：螺紋加工機床網> 技術（shù）前沿>數控（kòng）車床圓弧麵（miàn）螺紋車削研究與程（chéng）序開發（fā）

數（shù）控車床圓弧麵螺紋車削研究與（yǔ）程（chéng）序開發

2016-12-8 來（lái）源：四川（chuān）工（gōng）程職業技術學院機電工程係（xì）作者：彭美武西慶（qìng）坤（kūn）苟建（jiàn）峰鍾成明（míng）

摘要： 在車削直螺紋（wén）或錐螺紋功能基礎上，提出了采用（yòng）小線段螺紋插補實現圓（yuán）弧麵上螺紋車削的思想。為了求出逼近小線（xiàn）段坐標，采用幾何算法對圓弧的圓心進行計算，確定加工圓弧的起始角和終止角，然後通過坐標變換得到逼近小線段點相對工（gōng）件原點的坐標。最後結合ＳＩＮＵＭＥＲＩＫ數控係統的Ｒ參數功能，實現（xiàn）了圓弧麵螺紋車削的數控程序開發。

關鍵詞： 圓弧麵；螺紋插補；逼近；幾何算法；Ｒ參（cān）數

目前，幾乎所有數控車床都具有螺紋加工功能及（jí）相應的指令，如ＦＡＮＵＣ數控采（cǎi）用Ｇ３２、Ｇ９２或Ｇ７６指令（lìng），ＳＩＮＵＭＥＲＩＫ數控（kòng）係統（tǒng）采（cǎi）用Ｇ３３或（huò）ＣＹＣＬＥ９７指令實現螺（luó）紋的車削加工，但這些指令主要是直接對直螺紋或（huò）錐（zhuī）螺紋加工。像一些圓（yuán）弧麵蝸杆［１－２］類零件，采用車（chē）削方式可以明顯提高加工效率，但這需（xū）要在圓弧麵上（shàng）進行螺紋加工，而直接應用上麵的指令是無法實現的，需要複雜的技術處理（lǐ）。

因此，為了解決這個難題，方便對各類圓弧麵蝸杆類零件（jiàn）進行加工，有必要開發（fā）出圓弧麵螺紋（wén）功能指令，然（rán）後隻（zhī）需要調用該指令，並進行簡單數學及（jí）工藝方（fāng）麵的處理，可以方便地加工出此類零件。下麵介紹在ＳＩＮＵＭＥＲＩＫ數控係統中開發（fā）此功能（néng）的詳細過程。

１.圓（yuán）弧（hú）麵螺紋功能開發方案

以常見的加工三角形螺紋為例，如圖１所示（shì），在逆時針圓（yuán）弧ＡＢ上加工三角形螺紋，螺距為Ｐ，圓弧起點為（wéi）Ａ，終點為Ｂ，半徑為Ｒ。其中弧長ＡＢ包含（hán）加工螺紋時需要的引入段δ１、引出段δ２長度。以（yǐ）工件右端麵中心Ｏ為坐標原點。

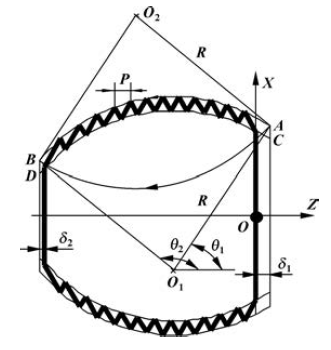
圖１　圓弧麵（miàn）螺紋示意圖

在逆時針圓弧（hú）ＡＢ上加工三角螺紋，一般可將圓弧ＡＢ細分成（chéng）若（ruò）幹（gàn）小的直線段逼近（jìn），然後應用Ｇ３３指令實現螺紋插補。每走一次循環，Ｘ方向進給一個深度（dù），直到加工到（dào）螺紋牙底，也就是從圓弧ＡＢ開始，加工（gōng）到圓弧ＣＤ。

要實現逆時針圓弧ＡＢ小線段逼近，最主要解決的問題是由已知條件算出圓弧（hú）的圓心Ｏ１，然後根據圓心可以方便確（què）定（dìng）每次進刀圓弧起點的起始角θ１和終止角θ２；同時由圓參數方程（chéng）確定出每（měi）次逼近線段相對圓心的坐標，通（tōng）過坐標（biāo）變換確定出（chū）每個逼（bī）近線段（duàn）點相對（duì）工件原點Ｏ的坐標尺寸，以便（biàn）於（yú）編程。

同理，也（yě）可以計算出通過圓弧（hú）起點為Ａ、終點為Ｂ、半徑為Ｒ的順時針圓弧ＡＢ的圓弧圓心Ｏ２，一樣可以計算出每個逼近線段（duàn）點相對工件原點Ｏ的坐標尺寸。

２.圓弧麵（miàn）螺紋功能開發過程

２.１　圓心及相關尺寸的計算

２.１.１　圓心的計算

已知一個圓弧兩（liǎng）點（diǎn）及半徑，求圓弧圓心坐標，滿足過這兩點的圓（yuán）弧有（yǒu）４個，圓心有２個，有順時針優、劣弧，逆時針優、劣弧。在數控車床，由於是回轉體零件以及車刀的角度問（wèn）題，一般（bān）不太可能是優弧，所以這裏隻討論劣弧對應（yīng）圓心的（de）計算問題，也就是確定圖１中的Ｏ１、Ｏ２。同時，在這裏隻研究（jiū）從右至左（zuǒ）加工螺紋。

通過兩（liǎng）點及半徑（jìng）求圓心，計算的（de）方法很多，比（bǐ）如帶入法、矢量計算法［３］、坐標變換法［４］、中垂線法等（děng），但這（zhè）些（xiē）方法計算（suàn）過程或（huò）公式相對較複雜，在這裏介紹一種幾何算法確定圓心［５］。如圖２所示是逆時（shí）針圓弧圓心（xīn）幾何算法原（yuán）理圖，連（lián）接線段ＡＢ，通過圓心Ｏ１向線段ＡＢ作垂線，交點為Ｍ，則Ｍ就是線段ＡＢ的中點。過點Ｍ、Ｏ１分別作平行於Ｘ軸、Ｚ軸的平（píng）行線（xiàn），交（jiāo）點為Ｅ；同樣過點（diǎn）Ａ、Ｂ分別作（zuò）平行於Ｘ軸、Ｚ軸的（de）平行線，交點為點Ｆ。很顯然△ＢＡＦ∽△ＭＯ１Ｅ，因此有：

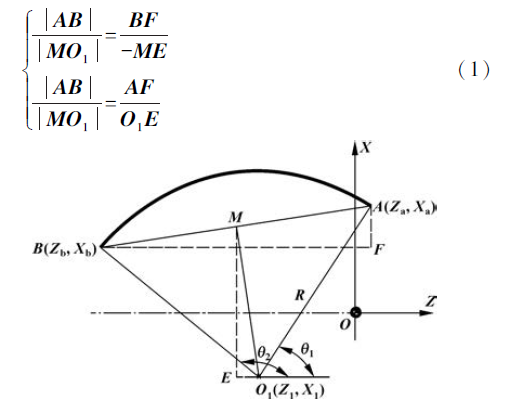
圖２　逆時針圓弧圓心（xīn）幾何算法原理圖

公式（１）中，不考慮左邊算式方向，右邊算式分子、分母均要考慮矢量方向，令Ｌ１＝ |ＢＡ |，Ｌ２＝

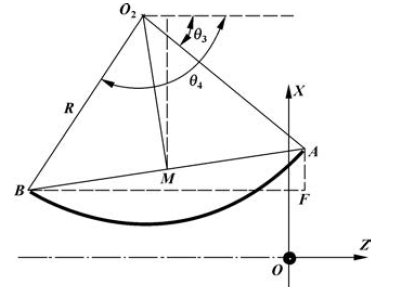
圖３　順時針圓弧圓心（xīn）幾何（hé）算法原理（lǐ）圖

公式（２）和公式（３）中計算圓（yuán）弧圓心Ｚ坐標時，如果Ｘａ＝Ｘｂ時，則無法計算，但是很明顯這時的Ｚ１＝ＺＭ，Ｚ２＝ＺＭ。因此，在程（chéng）序開發時需要先判斷Ｘａ與Ｘｂ是否相等。

２.１.２　圓弧起始角、終止（zhǐ）角的計算

為（wéi）了後續程序編（biān）製方便，在這裏采用圓的參數方程（chéng）求每點逼近線段坐標，因此需要確定圓弧的角度範圍，即要確定圖２中的θ１、θ２，圖３中的（de）θ３、θ４。由（yóu）圖２可得：

文2

２.１.３　逼近點坐（zuò）標計算

通過圓的參數方程求出（chū）每點（diǎn）逼近線（xiàn）段坐標時相對圓弧（hú）圓心的坐標，而（ér）在加工（gōng）過程中每點逼近線段（duàn）坐標應該是相對工件原點Ｏ的坐標值，因此這需（xū）要坐標（biāo）變換，得到編程需要的坐標。假如每次要用直（zhí）線逼近的圓弧半徑為Ｒ，則得到圓的（de）參數方程：

２.２　Ｒ參數（shù）程序設（shè）計

２.２.１　Ｒ參數變量定義及分析（xī）

ＳＩＮＵＭＥＲＩＫ數控係統Ｒ參數編程［６］和ＦＡＵＮＣ數控係統宏（hóng）程序編程一樣，通過對變量Ｒ進行賦值，再配合循環功能，可以方便（biàn）地實現變量的數學運算和邏輯運算，能解（jiě）決許多有規律性或較複雜零（líng）件的編程。

采用Ｒ參數定義變量，主要包含初始變量和中間變量，設定的主要初始變量如下：Ｒ０、Ｒ１：圓弧起點Ａ坐標（Ｘａ，Ｚａ）；Ｒ２、Ｒ３：圓弧終點Ｂ坐標（Ｘｂ，Ｚｂ）；Ｒ：圓弧ＡＢ半徑；Ｒ５：螺（luó）紋螺距；Ｒ６：設置（zhì）為２或３，分別代表順時針圓弧（hú）或逆時針圓弧。

通過初始變量需要計算的中間變量主要有：Ｒ７、Ｒ８：逆時針圓弧圓心坐（zuò）標（Ｘ１，Ｚ１）；Ｒ９、Ｒ１０：順時（shí）針圓（yuán）弧圓心（xīn）坐（zuò）標（Ｘ２，Ｚ２）；Ｒ１１、Ｒ１２：逆（nì）時針圓弧起始角（jiǎo）、止角θ１、θ２；Ｒ１３、Ｒ１４：順時針圓（yuán）弧起始角、終止（zhǐ）角θ３、θ４；Ｒ１５、Ｒ１６：逆時（shí）針圓弧逼近線段點相對工件原（yuán）點Ｏ的坐標（Ｘ，Ｚ）；Ｒ１７、Ｒ１８：順時（shí）針圓弧（hú）逼近（jìn）線段點相對工件原點Ｏ的坐標（Ｘ，Ｚ）。

為（wéi）了計算方（fāng）便，上述Ｘ坐標均表示半徑值。另外，為了簡化公式，將部分公式也設為中（zhōng）間變量：

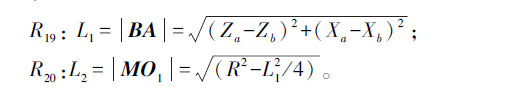
對於圓弧麵螺紋，每次（cì）Ｘ向進一層深度，每層（céng）圓弧的起點（diǎn）坐標和終點坐標是變化的，因此需要對每層圓弧的起始角、終止角（jiǎo）重新計（jì）算。根據分析，得到（dào）每層圓弧（hú）螺紋切削循環子程序流程圖如圖４所（suǒ）示，順時針、逆時針圓弧螺紋（wén）車削思路相同。

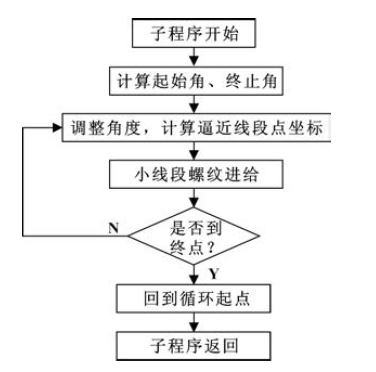
圖４　每層圓弧螺紋車削子程序流程圖

２.２.２　Ｒ參數程序設計

以圓弧麵螺紋螺距（jù）為２ｍｍ、牙深為１. ２９９ｍｍ為例（lì），像加工直螺紋一樣，按照經驗，推薦每次Ｘ向（xiàng）進給半徑（jìng）深度為０.４５、０.３５、０.２５、０.２、０.０５ｍｍ，Ｘ向每進一層深（shēn）度，調用一次螺紋（wén）加工子程序（xù）。為了保證每加工一層螺紋後，能安全退刀到一固（gù）定（dìng）點，同（tóng）時也是每次進（jìn）刀的起始點，這裏需要設置一個循環起點。循環起點的設置可以根據具體圓弧尺寸（cùn）設置，也可以設置（zhì）為（ＸＭ＋Ｒ，Ｚａ），可保證退刀時候不（bú）會打刀。

圓弧麵螺紋數控加（jiā）工主（zhǔ）程序如下：

ＹＨＬＷ.ＭＰＦ；主程序（xù）名

Ｔ１Ｄ１

Ｓ５００Ｍ０３

Ｒ０＝２０Ｒ１＝４Ｒ２＝２５Ｒ３＝－５０Ｒ４＝３０

Ｒ５＝２Ｒ６＝３；變量賦初始值，並設加工（gōng）逆時針圓（yuán）弧

Ｒ２１＝（Ｒ０＋Ｒ２）／２＋Ｒ４；定義循環起點Ｘ坐標（半徑值）

Ｒ１９＝ＳＱＲＴ（ＰＯＴ（Ｒ１－Ｒ３）＋ＰＯＴ（Ｒ０－Ｒ２））；計算Ｌ１

Ｒ２０＝ＳＱＲＴ（ＰＯＴ（Ｒ４）－ＰＯＴ（Ｒ１９）／４）；計算Ｌ２

Ｇ００Ｘ＝２*Ｒ２１Ｚ＝Ｒ１；刀具運動（dòng）到循環起點

ＩＦＲ６＝＝２ＧＯＴＯＦＳＲ；如果Ｒ６＝２，轉入加（jiā）工（gōng）順時（shí）針圓弧螺紋車削程序段；否則執行下麵逆（nì）時針圓（yuán）弧螺紋車削

Ｒ７＝（Ｒ０＋Ｒ２）／２－Ｒ２０／Ｒ１９*（Ｒ１－Ｒ３）；計算Ｘ１

ＩＦＲ０＝＝Ｒ２ＧＯＴＯＦＡＡ；判斷Ｘａ與Ｘｂ是（shì）否相等，相等則轉入ＡＡ程序（xù）段

Ｒ８＝（Ｒ１＋Ｒ３）／２＋Ｒ２０／Ｒ１９*（Ｒ０－Ｒ２）；計算（suàn）Ｚ１ＧＯＴＯＦＢＢ

ＡＡ：Ｒ８＝（Ｒ１＋Ｒ３）／２；計算（suàn）Ｚ１ＢＢ：Ｒ２２＝Ｒ０－０. ４５；計算第一（yī）層Ｘ向進給坐標

Ｒ２３＝Ｒ２－０.４５；圓弧終（zhōng）點Ｘ坐標調整

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第１次進刀

ＣＹＣＬＥ３５

Ｒ２２＝Ｒ２２－０.３５；

Ｒ２３＝Ｒ２３－０.３５

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第２次進刀

ＣＹＣＬＥ３５

Ｒ２２＝Ｒ２２－０.２５；

Ｒ２３＝Ｒ２３－０.２５

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第３次（cì）進刀

ＣＹＣＬＥ３５

Ｒ２２＝Ｒ２２－０. ２；

Ｒ２３＝Ｒ２３－０. ２

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第４次進刀（dāo）

ＣＹＣＬＥ３５

Ｒ２２＝Ｒ２２－０.０５；

Ｒ２３＝Ｒ２３－０.０５

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第５次進刀

ＣＹＣＬＥ３５

ＧＯＴＯＦＺＺ

ＳＲ：Ｒ９＝（Ｒ０＋Ｒ２）／２＋Ｒ２０／Ｒ１９*（Ｒ１－Ｒ３）；計（jì）算Ｘ２

ＩＦＲ０＝＝Ｒ２ＧＯＴＯＦＣＣ；判斷Ｘａ與Ｘｂ是否相等

Ｒ１０＝（Ｒ１＋Ｒ３）／２－Ｒ２０／Ｒ１９*（Ｒ０－Ｒ２）；計算Ｚ２

ＧＯＴＯＦＤＤ

ＣＣ：Ｒ８＝（Ｒ１＋Ｒ３）／２；計算Ｚ２ＤＤ：Ｒ２２＝Ｒ０＋０. ４５；計算第一層Ｘ向進給坐標

Ｒ２３＝Ｒ２＋０. ４５；圓弧終點Ｘ坐標調（diào）整

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向（xiàng）第１次進刀

ＣＹＣＬＥ３６

Ｒ２２＝Ｒ２２＋０.３５；

Ｒ２３＝Ｒ２３＋０.３５

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第２次進刀

ＣＹＣＬＥ３６

Ｒ２２＝Ｒ２２＋０.２５；

Ｒ２３＝Ｒ２３＋０.２５

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第３次進刀

ＣＹＣＬＥ３６

Ｒ２２＝Ｒ２２＋０.２；

Ｒ２３＝Ｒ２３＋０. ２

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第４次進刀

ＣＹＣＬＥ３６

Ｒ２２＝Ｒ２２＋０.０５；

Ｒ２３＝Ｒ２３＋０.０５

Ｇ００Ｘ＝２*Ｒ２２；Ｘ向第５次進刀（dāo）

ＣＹＣＬＥ３６

ＺＺ：Ｇ００Ｘ１００Ｚ１００

Ｍ３０

每層逆時針圓弧螺紋車削子程序程序如下：

ＣＹＣＬＥ３５．ＳＰＦ；

Ｒ１１＝ＡＴＡＮ２（（ＡＢＳ（Ｒ２２－Ｒ７），ＡＢＳ（Ｒ１－Ｒ８））；計算起始角θ１

Ｒ１２＝１８０－ＡＴＡＮ２（（ＡＢＳ（Ｒ２３－Ｒ７），ＡＢＳ（Ｒ３－Ｒ８））；計算終止角（jiǎo）θ２

Ｒ２４＝ＳＱＲＴ（ＰＯＴ（Ｒ２２－Ｒ７）＋ＰＯＴ（Ｒ１－Ｒ８））；計算進刀後的圓弧（hú）半徑

ＰＰ：Ｒ１１＝Ｒ１１＋０. １；角度遞增０. １°

Ｒ１５＝Ｒ２４*ＳＩＮ（Ｒ１１）＋Ｒ７；計算逼近線段（duàn）點相（xiàng）對工件原點Ｏ的Ｘ坐標

Ｒ１６＝Ｒ２４*ＣＯＳ（Ｒ１１）＋Ｒ８；計（jì）算逼近（jìn）線段點相對工件原點Ｏ的Ｚ坐標

Ｇ３３Ｘ＝２*Ｒ１５Ｚ＝Ｒ１６Ｋ＝Ｒ５；小線段螺紋插補

ＩＦＲ１１＜Ｒ１２ＧＯＴＯＢＰＰ；判斷是否（fǒu）到達終止角

Ｇ００Ｘ＝２*Ｒ２１；Ｘ向退刀循（xún）環起點的（de）Ｘ坐標（biāo）

Ｚ＝Ｒ０；Ｚ向退刀循環起點的Ｚ坐標

Ｚ＝Ｒ０；Ｚ向退刀循環起點的Ｚ坐（zuò）標Ｍ１７

每層（céng）順時針圓弧螺（luó）紋車削子程序程序如（rú）下：

ＣＹＣＬＥ３６．ＳＰＦ；

Ｒ１３＝－ＡＴＡＮ２（（ＡＢＳ（Ｒ２２－Ｒ９），ＡＢＳ（Ｒ１－Ｒ１０））；計算（suàn）起始（shǐ）角θ３

Ｒ１４＝ＡＴＡＮ２（（ＡＢＳ（Ｒ２３－Ｒ９），ＡＢＳ（Ｒ３－Ｒ１０））－１８０；計算終止角θ４

Ｒ２４＝ＳＱＲＴ（ＰＯＴ（Ｒ２２－Ｒ９）＋ＰＯＴ（Ｒ１－Ｒ１０））；計算進刀後（hòu）的圓弧半徑

ＰＰ：Ｒ１３＝Ｒ１１－０.１；角度遞減０.１°

Ｒ１７＝Ｒ２４*ＳＩＮ（Ｒ１３）＋Ｒ９；計算逼近線段點相對工件原點Ｏ的Ｘ坐標

Ｒ１８＝Ｒ２４*ＣＯＳ（Ｒ１３）＋Ｒ１０；計算逼近線段點相對工件原點Ｏ的Ｚ坐標

Ｇ３３Ｘ＝２*Ｒ１７Ｚ＝Ｒ１８Ｋ＝Ｒ５；小線段螺紋（wén）插補

ＩＦＲ１３＞Ｒ１４ＧＯＴＯＢＰＰ；判斷是否到達終止角

Ｇ００Ｘ＝２*Ｒ２１；Ｘ向退刀循（xún）環起點的（de）Ｘ坐標Ｚ＝Ｒ０；Ｚ向退刀循環起點的Ｚ坐標Ｍ１７

程序中Ｘ向每次（cì）進給（gěi）也可以用（yòng）Ｒ參數設定。同時，如果每次Ｘ向進（jìn）給（gěi）深度相同，程序將大大簡化，但現實加工並非如此。

3.結束語

通過對數控車床圓弧麵上螺紋車削（xuē）功能進行（háng）開發，為各類（lèi）圓弧麵蝸杆類零件車削提（tí）供了基礎平台，有了這個平台（tái），圓弧麵蝸杆類（lèi）零件車削程序將大大簡化，在實際（jì）生產中具有重要的意義。同時，該功能的開發思路與方法同樣適用於ＦＡＮＵＣ等其他各類數控係統，通過采用變量編程，能很好地實現這個功能。

投稿箱：
如果您（nín）有機床行業、企業相關新聞稿件發表，或（huò）進行資（zī）訊合作，歡迎聯係本網編（biān）輯部，郵箱：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視點

| 更多

行業數據

| 更多

博文選萃

| 更多