機器人的運動軌跡插值（zhí）方法研究與（yǔ）分（fèn）析-機器人-數控機床市場網

您現在的位置：機器人> 技術前沿>機器人（rén）的（de）運動軌（guǐ）跡插值方法研究與分（fèn）析

機器（qì）人的運動軌跡插值方法研究與分析

2016-12-5 來源：陝西理工學院陝西省工（gōng）業自動化重點實驗室作（zuò）者：趙川張鵬超潘曉磊呂（lǚ）海立

軌跡規劃對工業機器（qì）人能夠高效、穩定的（de）運動有重要的影響。機器（qì）人工作時必須保證運行軌跡的平滑。若各關節的速度和（hé）加速度突變或者不連續會在機器人（rén）工作過程中（zhōng），加劇機構的摩擦，機（jī）械臂出現振動現象，增大軌（guǐ）跡跟蹤誤差，降低跟蹤精度，縮短機器人的使（shǐ）用（yòng）壽命。為此學者們提出了多項式插值、B樣條曲線（xiàn）插值等插值方法，從而得到關節速度和加速度平穩、光滑且連續的軌跡。

本文通過在MATLAB環境中仿真研究了三次多項式與五次多項式插值後（hòu），各關節的關節角度位置、速度和加速度的變化軌跡（jì），通過研究分析提出了過（guò）路徑點的點到（dào）點（diǎn）運動間的“353”∽1多項式插值，並且得到了關節速度和加速度的平滑連續的變化軌（guǐ）跡。

1.機（jī）器人運動學模型

本文以NACHI的六自由度MZ07工業機器（qì）人作為模（mó）型研究，確定機器人的連杆D—H坐標參數，如表1所示，在MATLAB中（zhōng）構（gòu）建機器人的數（shù）學模型，如圖1所示。

表1 MZ07機器（qì）人連杆D—H參數

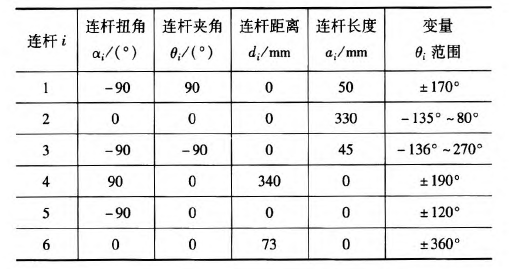
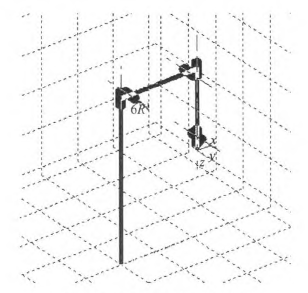
圖1機器人MATLAB=維（wéi）模型

2.關節空間軌跡插值研究

關節空間法是以含有關節角度的函數（shù）來描述機（jī）器人的軌跡，在進行關節空間軌跡（jì）規劃時，需要通（tōng）過運動學的逆解，將路徑點轉（zhuǎn）換成關節矢量角度值，再通（tōng）過對每個關節擬合一個光滑函數，使從起始點開始，依次通過所有路徑點，最後到達目標點。對於（yú）每段路徑，每個關節運行時間均相同，則保證了所有關（guān）節同時到達路徑點（diǎn）和目標點，此外，各個關節函數之間是相互獨（dú）立（lì）存在的（de）。采用關節空間法不需要在直角坐標係中描述兩個路徑點之間的路徑形狀，所以計算簡（jiǎn）單、容易，並且關節空間不會發生在直角坐標空間中的機構奇異性問題。

2．1過路徑點的三次多項式插值

在單個關節運動過程中，為了使其能都（dōu）平穩地運動，要求關節在起始（shǐ）點速度和目標點速度均要為（wéi）0，而且關節起始角吼已（yǐ）知，終止點所可由運動（dòng）學反解（jiě）求（qiú）得，則一個三次多項式可由起始點的關節角度、速度和（hé）終止點的關節角度、速度4個約束唯一確定。因此對三次多項式：

由上確定的三次多項式的係數可以代人式（shì）(1)、(2)中，分別可以得到單個關節此時刻的的關節角度、關節速度以及（jí）加速（sù）度。

但是在現實應（yīng）用中，要求規劃出過路徑（jìng）點的軌跡，然後（hòu）在經過路徑點時的機器人手臂末端狀態會有兩種情（qíng）況：一種情況是機（jī）器人手臂（bì）由起（qǐ）始點運動（dòng）到路徑（jìng）點時停留，即此時的（de）在（zài）路（lù）徑點處的速度為零，則可以直接使用前麵的三（sān）次多項式插值算法；另一種情況是機器人手臂由起始（shǐ）點運動到路徑（jìng）點時不做停（tíng）留（liú），此時的速（sù）度已（yǐ）經不再為零（líng），則該點再運動到目標（biāo）點或者下一個路徑點時，不能采用前麵的三次多（duō）項式算法，故上式需要推廣成（chéng）為具有任意約束速度的（de）三次多項式插值（zhí）。在過路徑點的軌跡中，可以把（bǎ）所有的路徑點看做是“起始點”或者“目標（biāo）點”，通過求解其逆解，得到各關節的關（guān）節矢量值，然後確定一（yī）個三次（cì）多項式插（chā）值函數，使（shǐ）各個路徑點平滑地連接起來（lái）。隻是此時的“起始點”與“目標點”處的速度不再為零。在確定此三次多項式的方法與前麵所述方法相同，隻是改變了速度約束，即：

對於各（gè）路徑點處的（de）關（guān）節速（sù）度，我們采用平均值法來確定，規定各（gè）路徑點間的運動時間均相（xiàng）等，路徑（jìng）點速度可根據兩側的軌跡的角速度（dù）取平均值。如果對於運動軌（guǐ）跡的要求更加嚴格（gé），則需要更高階的多項式對運動軌跡（jì）進（jìn）行插值。但不是（shì）階數越高越好，高階多（duō）項式軌跡會出現“龍格”現象。本文針（zhēn）對五次多項式（shì）進行研究。五（wǔ）次多項式可由6個約束唯一確（què）定（dìng），即（jí）在起始點和目標點規定了關節位（wèi）置、速度和加速度，從而來約束整個運動（dòng）軌跡（jì）。五次多項式（shì）即：

2．3仿真研究

在MATLAB中對MZ07機器人的運動（dòng）進行軌跡規（guī）劃仿真（zhēn），設有起始點A(一100，0，一300)、中間點曰（yuē）(325，225，100)和目標點C(235，300，400)。從A點運動（dòng）到B點用時1 s，從B點到c點用（yòng）時（shí）1 S，求得三（sān）點的（de）關節變量值，如表2所示。

表2軌跡（jì）點的關節角度

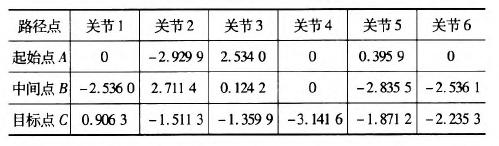
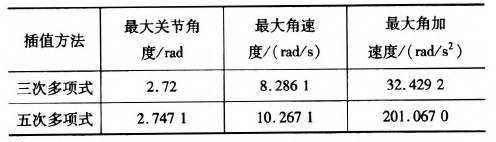
假定該運動的起始點與目標點的速（sù）度與加速度均為零。分別對該三點間的運動應用三次多項式插值和五次多項式插值，分別得到該過程中關節角度、速度和加速（sù）度的變（biàn）化（huà）情況，如圖2～7所示（shì），三次多項式與五次多項式插值後的關節角度、角速度和角加速（sù）度的產生（shēng）的最大值如表3所示。

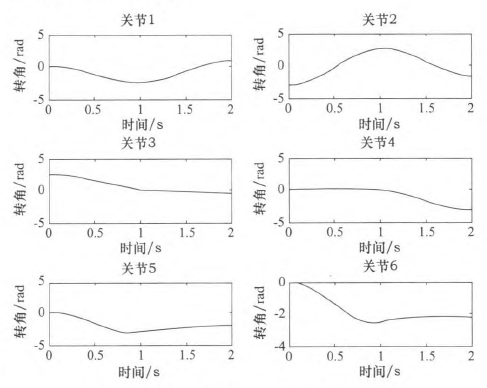
圖2三次多項式規劃後關節i一6角度位置

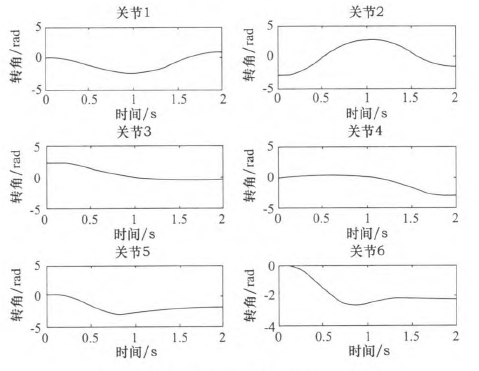
圖3五次多項式規劃後關節卜6角度位置

由仿真結果可知，三次和（hé）五次多項（xiàng）式都可以使（shǐ）運動軌跡平滑連續，但是三次多（duō）項式插值後，在關節加速度上出現（xiàn）突變，現實中機器人手臂在運動（dòng）中很可能無法完成此運動過程。五次多項式的加速度雖然可以光滑地連續起來，但是最大角加速度達（dá）到-j'201．067 0rad／s2，使運行不夠平穩緩（huǎn）和，也（yě）有害電動機的壽命。

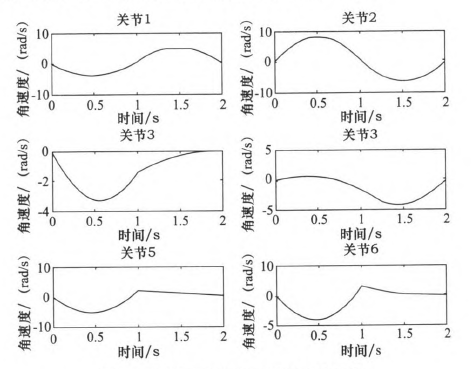
圖4 三（sān）次多項式規劃後關節1~6角速度

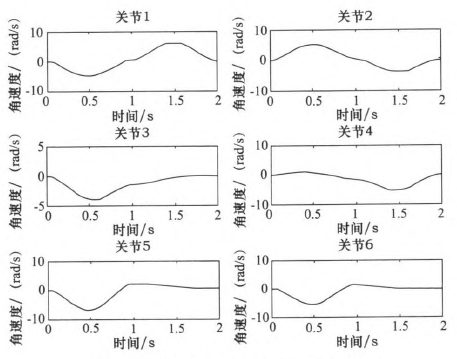
圖5 五次多（duō）項式規劃後關節1~6角速度

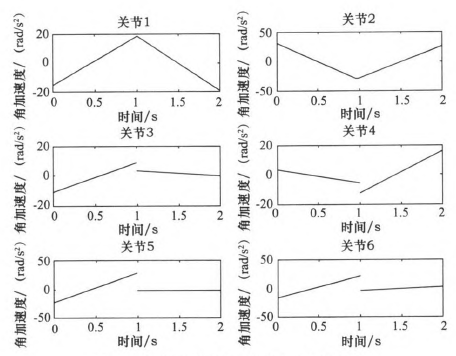
圖6三次多項（xiàng）式規劃後關（guān）節1-6角加速度

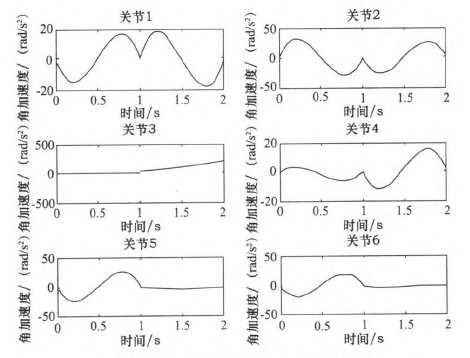
圖7五次多項式（shì）規劃後關節1～6角加速度

表3三（sān）次多項式與五次多項式最值比較

2．4過路徑點的“353”[gj多項式插值。

在實際對機器人運動軌跡規（guī）劃（huá）時，要求規劃過路徑點的軌跡，為了（le）得到加速（sù）度合適且連續、平滑的變化軌跡，介於三次多項式和五次多（duō）項式的優缺點，采用（yòng）了（le）“353”一1多項式插值，即三次多項式與五次多項式結合的（de）形式（shì）。如圖8所示，該方法將整個（gè）軌跡分為3個階段，第一階段為在0一t。時間內采用三（sān）次多項式插值，第二階段t。一t。時（shí）間內采用五次多項式插值，第三階段（duàn）t。一t，時間內采用三次多項式插值。本結構方法的要求，在兩個相鄰階段的交點處的關節角度、角速度和角加速度要求相等。其中t。、t6可分別取0一t^、t^一f，時刻的中間時（shí）刻。

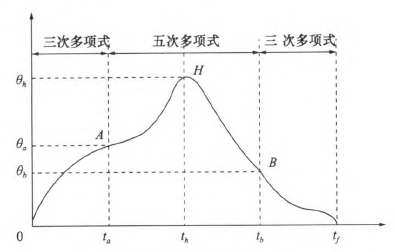
圖8“353”多項（xiàng）式結構

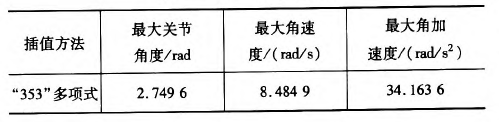
同樣使用2．3節假定的A、B、c三點。在MATLAB中（zhōng）仿真出“353”多項式結構算法規劃後的各關節的（de）關節角（jiǎo）度（dù）、角速度（dù）和角加速度變化情況，如圖9—10所示。規劃後的關（guān）節角度、角速（sù）度和角加速度的（de）最大值如表4所示。

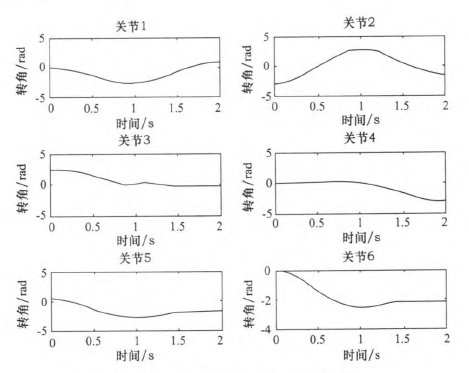
圖9 "353”多項式關節角度

根據仿真結束所示，該方法可以得到平穩、連續（xù）的關節角度、角速（sù）度和角加速度的變化軌跡。與（yǔ）表3中（zhōng）的三次、五（wǔ）次（cì）多項式最大值比較（jiào），可以看（kàn）出相（xiàng）對三次（cì）多項（xiàng）式可以得到平穩、連續的角加速度，同時相對五次多項（xiàng）式（shì）可以得到比較小的最大關（guān）節角（jiǎo）加速度，從而使整個關節運動過程中更加平滑，減小了機構間的衝擊（jī）。

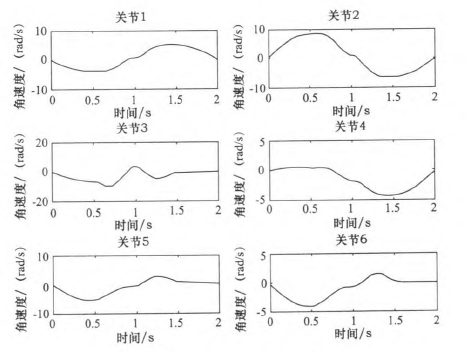
圖10 “353”多項式關節角速（sù）度

表4“353”多項式最值

3.結語

本文通過在MATLAB環境（jìng）中，基於MZ07工業機（jī）器人運（yùn）動模型，分析了三次多項式和五次多項式的軌跡插值算法，對比了兩個方（fāng）法的（de）優缺點。關節空間（jiān）在“353”多（duō）項式插值規（guī）劃後，通過仿真（zhēn）研究（jiū），“353”多項式插值既可以得到平穩、連續的角（jiǎo）加速度軌（guǐ）跡，又（yòu）可以（yǐ）得到較合適的最大角（jiǎo）加速度，解決了三次多項式插值後關節角加（jiā）速度不連續問題和五次多項式插值規劃後關節最大角加速度（dù）較大問題。在關節空間中（zhōng）多項式（shì）插值的高（gāo）低次結合使得各關（guān）節的變換優於單一使用的同次多項式插值。

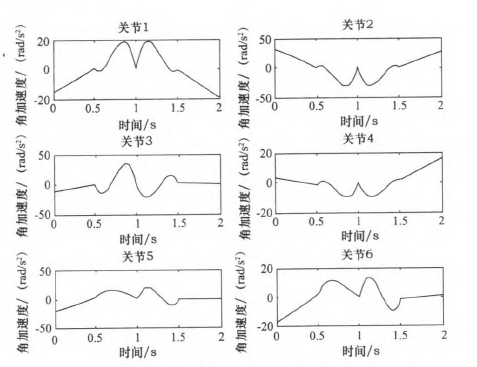
圖11 “353”多項式關節角加速度

投稿箱：
如果您有機床行業、企業相關新聞稿件發表（biǎo），或進行資訊（xùn）合作，歡迎聯係本網編輯（jí）部，郵箱：skjcsc@vip.sina.com

更多相關信息

名企推（tuī）薦

業界視點

| 更多

行業數據

| 更多

博文選萃

| 更多（duō）