基於遺傳算法的雙機器人加(jiā)工中心布(bù)局優(yōu)化
2016-8-18 來源:南京理X-大學 作者:王軍 曹春平 丁武學 孫宇
摘要:首先建立了麵向大型儀表板的雙機器人作業加工單元,為(wéi)了保證機器人和工件不發生碰撞,提出了以雙機器人(rén)的工作空間重合(hé)率最大為目標、基於遺傳算法的雙機器人加工(gōng)中心優化布局方法,建立了空(kōng)間約束的數學模型,利用MATLAB軟件進行仿真分析,並從空間重合率、加工周期兩個方麵進行比較(jiào)。結(jié)果表明:相對於公司(sī)現(xiàn)有狀(zhuàng)態,空間重合率提高了14.6%,加工周期縮短了1.2 min,驗證了(le)該方法的有效性和可(kě)行性。
關(guān)鍵詞:機器人;加工中心;布局優化;遺(yí)傳算法
0 、引言
近年來,機器人在工業領域已經被廣泛應(yīng)用,如焊接、鑽(zuàn)孔、裝配、運輸、噴塗等,尤其(qí)是在汽車製造領域。在汽車內飾領域,儀表板屬多型號小批(pī)量生(shēng)產(chǎn),不同型號儀(yí)表板上孔的位置、形狀、大小分布都不同,甚至差(chà)距很大。越來越多的企業引進(jìn)多機器人加工單元進行汽車儀表板的加工,以期在保證加工精度的前提下(xià)提高工作效率,縮短工作周期。多機器人加工(gōng)中心布局優化問題一直是國內外(wài)學者關注的重點。
在多機器(qì)人布局優化領域,Chedmail等[11通過修改(gǎi)機器(qì)人模型的D—H參數,並用八又樹表示機器人機器(qì)人工作空間和目標空間,同時引入避碰檢測來確(què)定加工中心(xīn)的布局;Kats[2。利用優化(huà)算法來求解所(suǒ)有無碰撞路徑的最小值,並以此為依據進行布(bù)局設計;Chittajallu等[31用圓形外包的方式描述布局設備,這種簡(jiǎn)化(huà)方式便於設備之間的幹涉檢驗,但布局空間不能得到合理有效的利用;Barral等H3提出了基於(yú)模擬退火算法的布局方(fāng)法,並在工業機器(qì)人軟件(jiàn)平台IGRIP上運用,由(yóu)於模擬退火算法本身的特性使得計算時間較長(zhǎng),布局方案計算耗時(shí)較(jiào)長;王召莉口3研究了機器人關節空間和操作空(kōng)間的特性,將機器人的關節軌(guǐ)跡距離作為評估指標,采用簡(jiǎn)單、高效(xiào)的自(zì)適應差分進(jìn)化(huà)算(suàn)法對典型機器人作業單元的布局優化實例進行研究。
本文以某企業典型的汽車儀表板為加工對象,研究麵向大型儀表板的雙機器人加工(gōng)中心的布局優化問題。目標為(wéi)在考慮兩(liǎng)個機器人和(hé)儀表板之間的位置關係基(jī)礎上保證機器人和工件不發生碰撞的前提下,使兩個機器人(rén)的工作空(kōng)間重合率最大(dà)。通過對機器人、工件進行數學建模,並引入相關約束條(tiáo)件(jiàn),利用遺傳算(suàn)法對雙機器(qì)人加工中心(xīn)的布局進行優化,最後(hòu)采用MATLAB軟件¨1進(jìn)行仿(fǎng)真分析,並從空間重合率、加工周期兩個方麵(miàn)進行比較(jiào)。
1、問題描(miáo)述(shù)與建模
1.1 問題描述
1.1.1儀表板的特點
汽車儀表板具(jù)有體積大、形狀複雜(zá)等(děng)特(tè)點,一般需要在銑削中(zhōng)心上完成多個孑L的加工。如圖(tú)1所示,儀表板上孔的位(wèi)置、形(xíng)狀、大(dà)小分布都不同,甚(shèn)至差距很大。此外,儀(yí)表板兩側孔的數量不同,一側孑L多(duō)一側孑L少,且在加工過程(chéng)中對象不能移動。若采用單個機器人加工則工作(zuò)空間有限,不能獨自完成(chéng)所有的任務,因此,需要至少兩個以上的機器人協調完成所有加工任務。

圖1某型(xíng)號儀表板
1.1.2加工中心的配置
根據汽車(chē)儀表板的加工特(tè)點,初步布置了雙機器人加工中心。兩個機器人分布在儀表板的(de)兩(liǎng)側,通過電機帶動機器人(rén)在導軌上左右移動,完成儀表(biǎo)板上所有工藝孔的加工,如圖2所示。
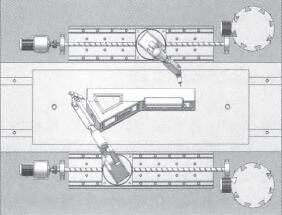
圖(tú)2 銑削加工中心布置示意圖
1.1.3方(fāng)案設計
在機器人布局設計中,在(zài)給定(dìng)機器人型號、尺寸的前提下,通過合(hé)理布局機器人(rén)和儀表板的位(wèi)置關係,提高兩個機器人的空間重合率,使孔較少一側的機器人在加工完本側的孑L後,能夠加工少量對麵的少量孔(kǒng),從而提高加工效率,以(yǐ)達到縮短生產周期的目的[7]。
1.2建模
1.2.1機器人建(jiàn)棋(qí)
一般來說,機器人前三個自由(yóu)度可以使機器人的末端執行器到達其工作空間內指定的任意位置(zhì),因此,可以(yǐ)隻考慮擁有(yǒu)前三個(gè)自由度的操作臂,至於(yú)末端姿態(tài)可以在工件外給定一個容許空間,用剩餘三個自由度來(lái)調整。單個(gè)機器人的模型簡圖見圖3。
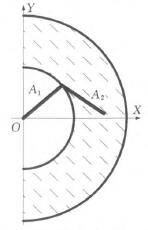
圖3單個機器人結構模型簡(jiǎn)化圖
如圖4所(suǒ)示,當機械(xiè)臂從點(diǎn)1運動到點2時(shí),機械(xiè)臂1一定會與工件發生碰撞,所以工件不能出現(xiàn)在半徑為A。的半圓內,因(yīn)此,機械臂有效工作空間為圖(tú)3所示的陰影(yǐng)部分,數(shù)學模型為R一{(z,y)l A;≤z2+Y2≤(Al+A2)2,z≥0} (1)
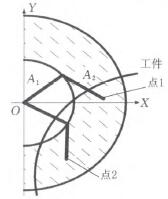
圖4 機械臂與工件一定會發(fā)生(shēng)碰撞的情況
1.2.2 工件建模
將儀表(biǎo)板向其橫截麵上投影,如圖5所示,加工對象所(suǒ)在的空間範圍簡稱為目標空(kōng)間,是由兩個半徑不同的扇形圍成的區域(yù)。
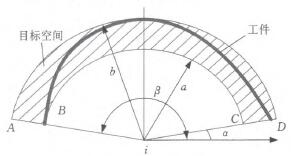
圖5 用(yòng)扇形區域表示工件
目標空間在極坐標係中表示(shì)為W一{(驢,10)l a≤妒≤盧,a≤P≤b/ (2)式(shì)中,a、b分別為(wéi)兩個圓弧的半徑;a、|9分別為目標空間在(zài)極坐標係(xì)中角度的極值。
因為在進行孔銑削時機器人末端執行器必須垂直於工件表麵,所以需要給定一容許空(kōng)間讓機器人調整末端姿態。因此,實際目標空間應當向(xiàng)外(wài)擴展一定距離,故目標空間中兩個圓弧的半徑分別為a+△L和b+AL。
1.2.3 約束模型(xíng)
要求兩個機器人同時對儀表板進行孔加工,加工中必須滿(mǎn)足兩個基本原則:①工件必須完全在兩個機器人的工作空間內;②必須提供足夠(gòu)的(de)空間(jiān),讓兩個機器人避免碰撞(zhuàng)。
為了滿足上述兩個原(yuán)則,建立三個坐標係:兩個機器人直角坐標係(xì)和一個工件極坐標係,通(tōng)過三個坐標係建立兩個機器人和工件(jiàn)之間的相對位置關係,如(rú)圖6所示,目標坐標係原點在兩個機器人(rén)的(de)直角坐標係中的坐標分別為(z,了)和(“,口),驢。和驢:為描述機器人加工(gōng)範圍的角(jiǎo)度值(zhí),其中儀表板在坐標係1一側孔較多,在坐標係2一(yī)側孔較少。
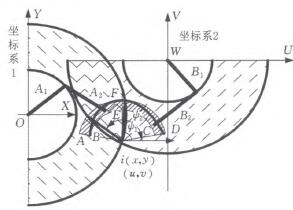
圖6 約束描(miáo)述

(1)約束一:目標空間必須在機器人工(gōng)作空間內。
要滿足約束一,點A、B必須在機器人1的加工範圍(wéi)內,點C、D必須(xū)在機(jī)器人(rén)2的加工(gōng)範圍內,即

同時(shí),孔多一側的機器人1可以加工所有本側的孔,則點E、F必須在機器人1的加工範圍內;孔(kǒng)少一側的機器(qì)人2有能力加工對側的孔,則點E、F必須在機器人2的加工範圍內。即
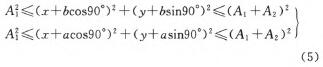
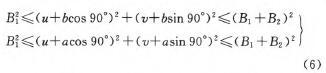
(2)約束二:A點不(bú)應該在機器人(rén)2的工作空間內部。一是為避免空間浪費,二是會造成兩個機器人距離太近,容易發生碰撞現象。

(3)約束三:為防(fáng)止機器人在姿態調(diào)整過程中與工件發(fā)生圖4所示的碰撞,工件的任一部(bù)分都不能出現在以A,為半徑的圓弧(hú)內,故應滿足如下(xià)條件:
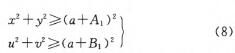
(4)約束四:兩機器人之間必須(xū)有足夠的(de)空間,以便兩個機器人的安裝、維修以及避碰等,即
其中,d需要設(shè)計者根據(jù)實際情況給出。
1.2.4 目標函數
優(yōu)化目標是在不發生(shēng)碰撞的(de)前提(tí)下,目標空間中(zhōng)兩個(gè)機器人的空間重合率盡量大。即
2、布局優(yōu)化算(suàn)法
上(shàng)述過程(chéng)將雙機器人加工中心(xīn)的布局問題轉變成非線性規劃問題。傳統的非(fēi)線性規劃算法的缺陷是計算煩瑣且精(jīng)度不高,穩(wěn)定性差,對函數初值和函數性態要求較(jiào)高,且容易陷(xiàn)入(rù)局部最優解。而遺傳算(suàn)法是一種全局搜索算法,可以克服傳統的非線性規劃算法容易陷入局部最(zuì)優解的(de)缺陷。因此,將遺傳算法應用於雙機器人布局優化問(wèn)題以改善收(shōu)斂效果,提高優化質量。
利用遺傳算法進行布局優化(huà)的步驟(zhòu)凹1如下:
(1)編碼。遺傳算法的編碼形式主要有二進製編碼和實數編碼,此處采用實數編碼。個體長度為6,4個描述位置關係的坐標值,2個描述機(jī)器(qì)人(rén)加工範圍的角度值。
(2)生成(chéng)初始群(qún)體。利用constraintdependen創建(jiàn)函數(shù)隨機地生成N一100個初(chū)始個體(tǐ),每個個體組合在一起形(xíng)成一個群(qún)體,遺傳算(suàn)法以這個(gè)群體作為初始種群(qún)進行迭代操作(zuò)。
(3)適應度(dù)函數的確定。本文通過遺傳算法求解兩個機器人的最大空間(jiān)重合率,相當於式(shì)
(10)所示的(de)目標函數。因MATLAB遺傳算法工具箱要求目標函數為求最小值,且最小值需為正值,因(yīn)此調整適應度函數為
繼而利用(yòng)工具箱提供的適應度的尺度變換函數排列(rank)來確定最終的適應度函數,以此為標準評價個體解的好壞來引導搜索,使適應(yīng)度函數最小化。
(4)選擇操作。本文采用輪盤賭選擇法(rou—lette函數)實現,假定個體i的適應(yīng)度值為(wéi).廠:,則其被選擇的概率P,為

(5)交叉操作。由於個體采用了實數編碼方式,所以交叉(chā)操作也采(cǎi)用實數交叉法,這裏采用(yòng)基於實(shí)數編碼的交叉(chā)算子為算數交叉(ArithmeticCrossover)。假(jiǎ)設兩個個體XA、X。之間進行算數交叉,則交叉後產生所(suǒ)產生的新個體為(wéi)

(6)變異操作(zuò)。因為上文(wén)采用的是實數編碼(mǎ)方式,此處采用均勻變異算子(uniform)進行變異操作。假設一個(gè)體為(wéi)x一(X。,X。,X。,X。,X。,X。),X。為(wéi)其中要變異的基因,則變(biàn)異操作如下:

(7)循環。重複步驟(2)至步驟(6)直到滿足終止條(tiáo)件(jiàn)。
(8)以最好的染色體(tǐ)作為最優解。
3、實例和結果分析
3.1 仿真實例優(yōu)化(huà)布局結果(guǒ)
以(yǐ)圖1所示型號(hào)儀表板為加工對象,並(bìng)取廠內某型號的(de)兩個機器人做實(shí)例分析,可得到兩個機器(qì)人的機(jī)械臂尺寸及工件模型的相關參數。
(1)已知條件。機械臂1的長度:A,一682 mm;A2—732 mm;機械臂2的長度:B1—1023 mm;B2—1145 mm;工件模型:a=987 mm;b一765;d一10。;盧一170。。
(2)6個變量。極坐(zuò)標係原點在兩(liǎng)個直角坐標係裏的坐標:(z,y)和(“,口(kǒu))。描述機器(qì)人加工範圍的角度值:驢。,≯:。
通過(guò)遺傳算法(fǎ)進行優(yōu)化求解(jiě),優(yōu)化後的布(bù)局結(jié)果見表(biǎo)1。
表1 布局優化結果
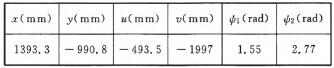
根據表1的優化結果,可得到極坐(zuò)標係原點在兩個機器人坐(zuò)標係中的(de)坐標(biāo)值,從而確定了兩個機器人和工件的(de)一個較優的位置關係(xì):

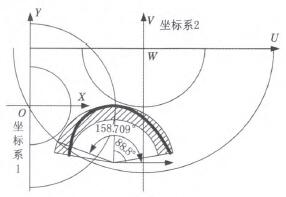
圖7 買(mǎi)際布局
3.2 仿真結果分析
根據仿真結果,對兩機器人進行重新(xīn)布局後,從機(jī)器人工(gōng)作的重合空間和加工周期兩個角(jiǎo)度進行分析,驗(yàn)證了(le)算法的(de)有效性。
3.2.1 重合空(kōng)間大小的比較
由布局優化結果得出兩機器人的加(jiā)工範圍f圖8)及幣合(hé)空(kōng)間的大小:
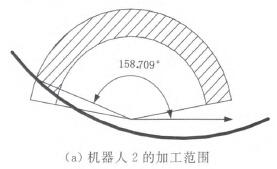
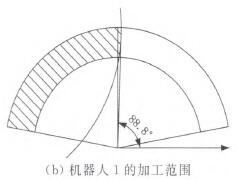
圖8 機器人的加工範圍
重合空間最大即驢z一≯,一69.9。。與實際機器(qì)人加工中心作比較,結果見表2。
表2 重合空間的比
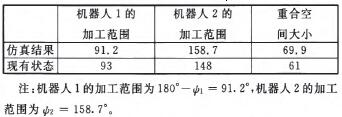
可以看出,在兩個(gè)機(jī)器人能完成各自任(rèn)務的(de)前提下,仿真(zhēn)結(jié)果(guǒ)表明此方法可以(yǐ)顯著提高兩個機器人(rén)的空間重合率(lǜ)。
3.2.2 加工周期的比較
(1)以圖1所示型號(hào)儀表(biǎo)板(bǎn)為對象,以兩個機器(qì)人加工時間相等為目標進行機器人加工任務的分配‘9|,如圖9所示。
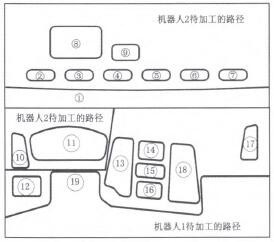
圖9 任務分配的結果
(2)在(zài)任(rèn)務分配的基礎上,以兩個機(jī)器人的運動路徑最短為(wéi)原則確(què)定銑削加工順序。該問題(tí)是典型的TSP問題,因此采用蟻群算法‘101來實現路(lù)徑優化仿真,得到(dào)的優化路徑如圖10所示。
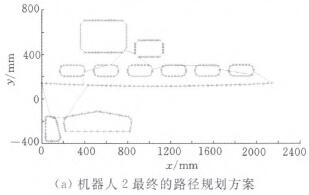
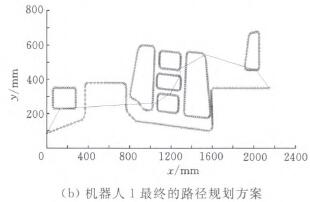
圖10 兩個機器人的路徑規劃方案
基於(yú)MATLAB平(píng)台利用Robotics Toolbox工具箱實現對工業機器人的係統仿真(zhēn)。為方便數據統計及實現自動輸出,設(shè)計機器人加工中心控製器,如圖11所示。根據(jù)上(shàng)述路徑(jìng)規劃結果以及(jí)時間最優(yōu)軌跡規劃,仿真得(dé)出機器人加工中心在(zài)加工過(guò)程中的總時間,並與現有的加工周期進行對比(bǐ)。

圖11 仿真控製器
仿真後得到(dào)單個儀表板的加工時(shí)間t。與工廠實際加工周期t。作比較,結果見表3。
表3加工周期的比較
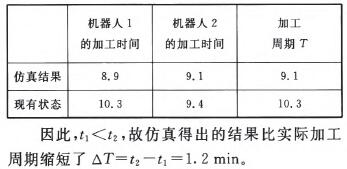
4、結語(yǔ)
本文通過對雙機器人(rén)加工(gōng)中心建立數學模型,引入相關約束。結(jié)果表明,該數學模型可以(yǐ)準確描述兩個機器人和儀表板之間的位置關(guān)係,為後續的仿真及布局奠定基礎。
遺傳算法是一種全局搜索算法,可以有效解決傳統非線性算法容易陷入局部最優解的問題,成功求解雙機器人加工中心的(de)最佳布局。
從仿(fǎng)真結果可(kě)以看出,通過該數學模(mó)型(xíng)和遺傳算法的有效結合,可以顯著提高兩個機器人的空間重合率,為後(hòu)續進行加工中心的(de)任務分配及路徑規劃提供較大的靈活(huó)性,從而達到最小化加(jiā)工周期的目標。
投稿箱:
如果您有機床行業、企業相關(guān)新聞稿件發表,或進行(háng)資訊合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關(guān)新聞稿件發表,或進行(háng)資訊合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相(xiàng)關信息
業界視點
| 更多
行業(yè)數據
| 更多
博文選萃
| 更多
- 機械加工過(guò)程圖示
- 判斷一台加工中心精度的幾種辦法
- 中走絲線切割機(jī)床的(de)發展(zhǎn)趨勢(shì)
- 國產數控係統和數控機床何去何從?
- 中國的技術工人都去哪裏了?
- 機械老板做了十多(duō)年,為何還(hái)是小作坊?
- 機械行業最新自殺性營銷,害人(rén)害己(jǐ)!不倒閉才
- 製造業大逃亡
- 智能時代(dài),少談點(diǎn)智造,多談點製造
- 現實麵前,國人沉默。製造業的騰飛,要從機床(chuáng)
- 一文搞懂數(shù)控車床加工(gōng)刀(dāo)具補償功能
- 車床鑽孔(kǒng)攻螺紋加工方法及工裝設計
- 傳統鑽削與螺旋銑孔加工工(gōng)藝的(de)區別





