考慮傳感器（qì）故障檢測能力的 PHM 係（xì）統傳感器優（yōu）化配置方法-機床（chuáng）電器網-數控機床市場網

您現在的位置：機床電器網> 技術前沿>考慮傳感器故障檢測能力的 PHM 係（xì）統傳感器優化配置方（fāng）法

考慮傳感器故障檢測能力的 PHM 係統傳感器優化配置方法（fǎ）

2015-2-24 來源：空軍工程大學陝西飛機工業集團等作者：朱喜華李（lǐ）穎暉侯世芳晏海波

摘要: 傳感器優化配置是航空航天設備 PHM 係統功能得以有（yǒu）效（xiào）實現的（de）基礎和保證。針對目前傳（chuán）感器（qì）配置研究中未考慮傳感器實際屬性的問題（tí），建立了考慮傳感器故（gù）障檢測能力的 PHM 係統傳感器優化配置模型。首先分析了係統故障（zhàng）－傳（chuán）感器（qì）相關性矩陣的含義，將傳感器的故障檢測（cè）能力和相關性矩陣（zhèn）相（xiàng）結合，以概率形式描述（shù）了傳感器對故障的（de）檢測性能（néng）。在此基礎上根據係（xì）統（tǒng）的測試性指標要求建立傳感器優化配（pèi）置模型，並采用（yòng）混沌二進製粒（lì）子群優化算法求解。仿真（zhēn）實例結果表明，本文建立的優化模型更加（jiā）符（fú）合實際情況，配置結（jié）果更加準確和可靠。

引言

傳感器優化配置是係統測試性設計的重（chóng）要內容，也是故障預測與健康管理(Prognostics andHealth Management，PHM) 係統的基礎，對 PHM係（xì）統功能的實現具有至關重要的作用。傳感器優化配置需要解決以下兩個問題:(1) 在保證（zhèng）係統故障覆蓋和辨識的前提下，確定需要（yào）采用的傳感器的類型和數目;(2) 對選定傳感器的布局進行優化，其優化準則（zé）是在保證係統（tǒng）具有較高可靠性（xìng）的前提下具有較好的檢測性能。從理論上講，傳（chuán）感器數量越多所（suǒ）獲取的係統性能參數就（jiù）越多，對係統健康狀態的描述就（jiù）越準（zhǔn）確越全麵。然而對於航空航天設備PHM 係統這樣的大型複雜係統，其監測變量成千（qiān）上萬，由於結構特點和經濟因素等（děng）原因的限製，不（bú）可能對所（suǒ）有變量都安（ān）裝傳感器進行測量。此（cǐ）外，傳感器的安裝和布局方式可能會對設備（bèi）的工作狀（zhuàng）態產生影響。因此，在滿足 PHM 係統測試性指標要求（qiú）的條件下，研究其傳（chuán）感器優化配置的理論和方法，選擇在其最關（guān）鍵的位置配置合適數量的傳感器，具有十分重要的理（lǐ）論意義及工程（chéng）實用價值。

近年（nián）來（lái），國內外（wài）學者對傳感器優化配置問題（tí）開展了廣泛的研究。BHUSHAN 等人提出了基於符號有向圖(SDG)在可靠性準則下的傳感器分布設計問題，其設計思（sī）想是從係統可靠性（xìng）最（zuì）薄弱的環節入手，以解決係統整（zhěng）體的可靠性問題;Bagajewica提出了一個混合整數（shù）線性規劃(Mixed Integer LinearProgramming，MILP) 模型以解決傳感器的選（xuǎn）擇問題，但是沒有考（kǎo）慮傳（chuán）感器（qì）故障的影響;清華大學的楊帆研究了利用概率符號有向圖(SDG)模型（xíng）來描述大規模複（fù）雜係統故障檢測的可靠性問題，並針對係統中（zhōng）各種傳感器的不同故障概率（lǜ），分析傳感器的（de）選（xuǎn）擇（zé）和分布對故障檢測可靠性（xìng）的影響;哈爾濱工業大學的（de）徐敏強針對某衛星一次電源係統，提出了一種基（jī）於可觀測性（xìng）和可靠性的傳感器分布優（yōu）化設計方法。

以上對於傳感器優（yōu）化配置的研究都沒有考慮傳感器自身的（de）故障檢測性能，都是假設傳（chuán）感器正常工作時能以（yǐ） 100% 的概率對相應的故障進行檢測，而這種假設是不符合實際（jì）情況（kuàng）的。實（shí）際工作（zuò）過程中，傳感器也有一定的故障率，其故障檢測能力除受自身性能的影響外，還與環境因素密切相（xiàng）關（guān），是各種因素綜合作用的結果。本文在他人研究的（de）基礎上，在建立優化模（mó）型時把傳感器的故障檢（jiǎn）測（cè）性能考慮在（zài）內，以增加（jiā）傳感器優化配（pèi）置結果的準確性和可靠性，並（bìng）以阿波羅號發射前的檢測為例進行了仿真驗證。

1 、係統故障－傳感器相關性矩陣

PHM 係統狀態監測（cè）和故障診斷的質量很大程（chéng）度上（shàng）依賴於（yú）傳感器所采集的信息，如果傳感器配（pèi）置不當（dāng），可能導致（zhì）某些故障無法（fǎ）檢測或對其不敏感，以（yǐ）致造成嚴重後果，因此傳感器的配置方（fāng）案必須（xū）保證對（duì）設備故障狀態的全（quán）部（bù）覆蓋和有效（xiào）辨識。這就要求對設備的故障模式具有一定的先驗知識，進而基（jī）於設備的故障模式分析進行傳感器優化配置，設備的故障模式（shì）可以（yǐ）通過對其進行故障（zhàng）模式影響及危害（hài）分析(Failure Modes，Effects and Criticality Analysis，FMECA)得到。為實現對設備故障模式的檢測和辨識，首先需要建立（lì）故障模式集（jí）合與傳感器集合之間的（de）相關性矩陣。

設某係統有 m 種故障模式，可供選擇的傳感器測量信號有 n 類（lèi），則該係統的故障－傳感器相關性矩陣（zhèn）可記為布爾邏輯矩陣 D = ［ dij］，其（qí）中 i = 1， 2，…， m， j = 1， 2， …， n。矩陣（zhèn）行表示故障模式，列表示傳感器類型，如（rú）表 1 所示。

表 1 故障－傳感器相關（guān）性矩陣

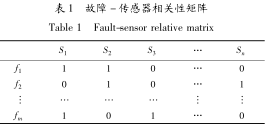
表 1 中，元素 dij= 1 表示故障 fi能被傳感器 sj檢（jiǎn）測到，元素 dij= 0 表（biǎo）示（shì）故（gù）障 fi不能被傳感器 sj檢測到（dào）。故障－傳感（gǎn）器相關性矩陣（zhèn）描述了係統故障與傳感器的二元（yuán）相（xiàng）關性關係，是對複雜係統進行（háng）傳感器優化配（pèi）置的基礎。

2 、傳感器故障（zhàng）檢測能力分析

係統（tǒng）故（gù）障－傳感器相關性矩陣隻是粗略地描述了係統故障集和（hé）傳感器集之間的簡單對（duì）應關係，其元素 dij= 1 可以有兩（liǎng）種含義:(1) 傳感器 sj能檢（jiǎn）測到故障（zhàng） fi的（de）發（fā）生，即二者有相關關係;(2) 當（dāng）故障fi發生時，傳（chuán）感器sj檢測到fi的概率為1，即隻要故障fi發生（shēng），傳感器 sj就能檢測到。同理（lǐ）可得 dij= 0 時的含義。顯（xiǎn）然，第一種含義更合理（lǐ），第二種含（hán）義則不符（fú）合（hé）實際情況。在實際係統中，由於傳感器自身的可靠性問題及（jí）環境因素的影響，即使（shǐ） dij= 1，傳（chuán）感器 sj也（yě）不一定能檢測到故障（zhàng） fi的發生。

傳感器對故障的檢測能力取決於多種因素，如（rú）傳感器的可靠性(故障率)、信（xìn）噪比、靈敏度等。定義傳（chuán）感器 sj對故障 fi的檢測能力如下:

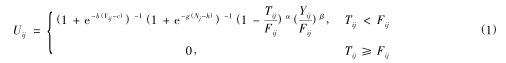
其中: Vij為傳感（gǎn）器 j 對故障 fi的檢測靈敏度;Nj為傳感器（qì）j的（de）信噪比;Tij為故障fi的發（fā）生時刻與傳感器 j 檢（jiǎn）測到該故障（zhàng）的時刻之間的時間間隔;Fij為故障 fi發（fā）生的（de）時刻與該故障導致（zhì）係統不能正常工作時刻之間的間隔;Yij為傳感器j能檢測到故（gù）障fi的征兆的持續時間;b、c、g、h、α和 β為（wéi）常數。由式(1) 可知，傳感器的故障檢測能力為(0，1) 之間的實數，可以理解（jiě）為檢測的（de）概（gài）率值。

根據經驗，典型的傳感器故障檢測能力可描述為（wéi）如下形式:

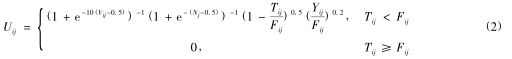
由於實際的傳感器具有一定的（de）故障率，在工程（chéng）實際中，對於一些重要變量的監測需要設置傳感器（qì）冗餘，即對於同一監測變量用多個傳感器測量，以提高故障檢（jiǎn）測的（de）可靠（kào）性，在本文（wén）的研究（jiū）中不考慮冗餘，即隻考慮傳感器是否（fǒu）安裝。假設各類傳感器（qì）的安裝數（shù）量為 Q = {q1，q2， …，qn}， qj∈ {0，1};各傳感器的故（gù）障率為λ = {λ1，λ2，…，λn}。綜合係（xì）統故障－傳（chuán）感器相關性矩陣和傳感（gǎn）器故障檢（jiǎn）測能（néng）力，在傳（chuán）感器不發生故障（zhàng）的條件下，當故障 fi發（fā）生時（shí），傳感器 sj對其進行有效檢測的能力為:

3 、傳感器配置優化模型的建立及（jí）求解

3． 1 優化模型的建立

傳感（gǎn）器優化配置就是在滿足係統各種測試性指標要求的前（qián）提下，選擇盡可能（néng）少的傳感器，使成本最小，同時滿足（zú）係統的故障檢測可靠性要求。假設係統各故障模式的（de）先驗概率集為 P = {p0，p1， …，pm}，且有∑mi =0pi= 1，其中 p0為正常狀（zhuàng）態的概率值。PHM 係統要求傳感器配置方案（àn）對係統所（suǒ）有故障模式的覆蓋，即對於每一種故障（zhàng） fi，都要有至（zhì）少一個傳感器對其進行檢測，數（shù）學描述為:

此外，PHM 係統對故障檢測率、故障隔離率和虛警率都有一定（dìng）的要求，分別如式(5)、(6)和(7)所示:

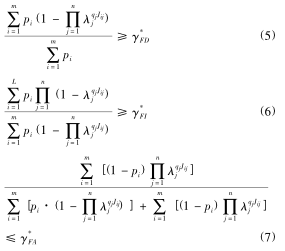
一個（gè）最優的傳感器配置（zhì）不僅要求能夠檢（jiǎn）測到被監控係（xì）統所有的故障，還要盡可能提高故障檢測的可（kě）靠性。故障檢測可靠性可以描述為:當係統發生某種故障時，其相關傳感器至少有一個（gè）正常工（gōng）作，保證能檢（jiǎn）測到該故障的發生;如果該（gāi）故（gù）障的所有相關傳感（gǎn）器都同時發生了（le）故障，則該故障不能被有效（xiào）檢測，即發生漏檢，從而導（dǎo）致故障檢測的可靠性降低。對於故障 fi，構造其故障檢測可靠性函數如下:

類似故障（zhàng）檢測率，用平均值來描述係統的故障檢測可（kě）靠性，該值（zhí）越小，故障檢測可靠性越高，如式(9)所示:

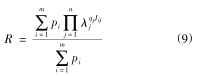
對於大型複雜係統，需（xū）要安裝的傳感器數量（liàng）極其龐大，成本是一個必須考慮（lǜ）的因素，主（zhǔ）要包括傳感器的購買、安裝（zhuāng）、維護，以及相應的數據采集（jí）和處理（lǐ）費用等（děng）。假設（shè）折算到每一個傳感器的成本為 cj，則總的成本為:

PHM係統（tǒng）傳感器優化配置的目的是在滿足係統測試性指標（biāo）(故障檢測率、故障隔離（lí）率等)的前提下，配置盡（jìn）可（kě）能（néng）少的傳感（gǎn）器（qì），使係統的總（zǒng）成本最低，同時滿足係統的可靠性要求，則優化模型為在滿足（zú）約束條件(4) ～ (7)條件下，使目標函數(9)和(10)取最小值。

3． 2 二進製粒子群算法的（de）混沌改（gǎi）進

傳（chuán）感器優化配置是（shì）一個集合覆蓋和多目標組合優化問題，屬於（yú）典型的 N- P 難題，許多文獻都（dōu）提出了相應（yīng）的求解方（fāng）法（fǎ），如基（jī）於邏（luó）輯運算的方法、基（jī）於貪婪策略的方法、基於遺傳算法（fǎ）的方（fāng）法和基於粒子群算法等，並在工程中得（dé）到了廣泛的應用（yòng）。粒子群算法(PSO)由於具有參數少、收斂速度快等優點，本文利用其改進離散形式（shì）— — —混沌二進製粒子群算法對傳感器優化模型進行求解。

基本（běn）粒子群（qún）優化算法中各粒（lì）子按式（shì）(11)更新（xīn）其速度和位置信息:

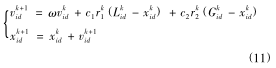
二進製粒子（zǐ）群算法中的速度向量不再是位置變化，而是（shì）作為粒子位置取 1 或 0 的概率。根據速度的大小來選擇粒子在對應位置上為 1 或 0，表（biǎo）示該位置上是否安裝傳感（gǎn）器（qì），其概率值（zhí）可以用 sigmoid 函數來描述:

為了防止 sigmoid 函數出現飽和（hé），將粒子的速度設（shè）定在一定範圍之內，其修改形式如下所示:

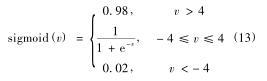
二（èr）進製粒子群算法粒子的（de）位置更新規律為:

式(14)中， δk+1id 為(0，1) 之間（jiān）的（de）隨機數。混沌優化方法（fǎ）是一種新穎的優化方法，它利用混沌係統特有的遍曆性特點來進行優化搜索，而且不要（yào）求目標函數具有連續和可微（wēi）的性質，其基本思想是首先產生一（yī）組（zǔ）與優化變量相同數（shù）目（mù）的混沌變量，用類似載波的方式（shì）將混沌（dùn）引入優化變量使其呈現混沌（dùn）狀（zhuàng）態，同時（shí）把混沌運動的遍曆範圍放大到優化變量的取值範圍然（rán）後直接利（lì）用混沌變量（liàng）進行搜索。一般應用 Logistic 映射(邏輯（jí）映射)來產生混沌變量（liàng），其映射形式如下:

其中μ ∈［ 0，4］為控製變量，zk∈［ 0，1］，k =0，1， 2，…。當 μ = 4 時，係統完（wán）全處於混沌狀（zhuàng）態，此（cǐ）時，軌道布滿區間［ 0，1］，即混沌軌道在區間［ 0，1］內遍曆。由任意初值（zhí） z0∈［ 0，1］可迭代出一個確定的混沌時間序列 z1，z2，z3， …。

4 、仿真實例（lì）分析

以中（zhōng）阿波羅號發射前（qián）的檢測為例，根據上述方法進行仿真分析。該係統有（yǒu） 10 種故障模式，可提供 15 個傳感器（qì）測量點。假設係統的故障檢測率、故障隔離率要（yào）求（qiú）分（fèn）別為不低於 90% 和 85%，虛警率要求不高於 5%。該係統的部分故障－傳感器相關性矩陣 (S1－ S10) 如表 2 所示（shì），故障（zhàng）先驗概率和各傳感器成本分（fèn）別見表 3 和表 4。

根據（jù）本文的（de）混沌二進製粒子群（qún）算法對建立的傳感（gǎn）器優化配置模型進行求解，結果為:各傳感器配置數（shù）量為［ 1，0，0，0，0，0，0，0，1，0，1，0，0，1，0］，故障檢測率為 95．2%，故障隔離（lí）率為 91．5%，虛警率為 3．7%，故障檢測可靠性指標為 0．0368，總成本（běn）為 1．1。文獻13］的配置（zhì）結果為:各傳感器配置數量為［ 0，0，0，0，0，0，0，0，0，0，1，0，0，1，0］，係統故障檢測率 100%，故障隔（gé）離（lí）率為 100%，總成本為 0．7。

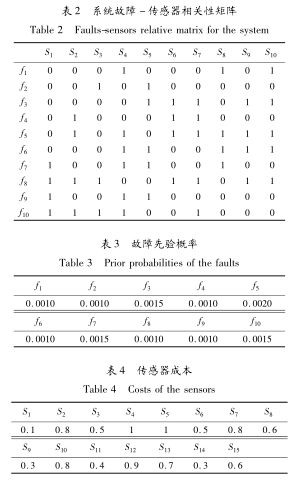
由仿真計算（suàn）結果可知，各項性能（néng）指標都能滿足係統的要求。跟的結果對比分析得: 本文方（fāng）法要（yào）比多安裝傳感器 S1和 S9; 故障檢測（cè）率（lǜ）、故障隔離率結果都較有所降（jiàng）低，但都能滿足係統的故障診斷要求（qiú）。導致這一結（jié）果的原因有:(1) 本文建模時將故障檢測可靠（kào）性作為一個優化的性能指標;(2) 本文模型考慮了傳感（gǎn）器對故障的檢測性能，即傳感器對故障的檢測能力不是簡單的0 或者1，而（ér）是介於 0 和 1 之間的實數（shù）。由（yóu）於考慮了傳（chuán）感器檢測故障能力的實際（jì）屬性，本（běn）文建立的模型更加符合實（shí）際情況（kuàng），優化結果也（yě）更加準確和可靠（kào）。

5 結論

信息獲取（qǔ）的完備性和準確性是 PHM 係統功能有效實現（xiàn）的基礎。隨著航空航天技術的飛（fēi）速發展，航空航天設備的功能日益強大，複（fù）雜性也越來越高，為了對其工作狀況和健康狀態（tài）進行實時監測，需要安裝大量的傳感器以采集其各（gè）種信息。大型（xíng）複雜設備具有數（shù）量龐大的監測變量，對（duì）其進行有效（xiào）的選擇性測量顯得尤為重要，這就需要在係統設計（jì）之初就對傳感器的選（xuǎn）擇和配置進行全局優化，安裝盡可能少的傳感器對其關鍵變量進行監測，以滿足係統的（de）PHM 要求。本文在參考他人研究的基礎上，將傳感器的故障檢測能力加入優（yōu）化配置模型之中，用概率的形式對傳感器（qì）的（de）故障（zhàng）檢測性能進行描述:傳感器的故（gù）障（zhàng）檢（jiǎn）測（cè）能力不是係統故障－傳感（gǎn）器相關性矩陣中簡單的 0 或者（zhě） 1，而是介於 0 和 1 之間的實數，具體取決於傳感器的可靠性(故障率)、信噪比、靈敏度等和（hé）環境因素等多種因素（sù）。仿真實例（lì）結果說明了本文方法的可行性（xìng）和（hé）準確性，對航（háng）空航天設備 PHM係統的傳感（gǎn）器優化（huà）配置具有（yǒu）參（cān）考價值。

投稿箱：
如果您有機床（chuáng）行業、企業相（xiàng）關新聞稿件發表，或進行資訊合（hé）作，歡迎聯係本網編輯部，郵箱：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視點

| 更多

行（háng）業數（shù）據

| 更（gèng）多

博文選萃

| 更多

數（shù）控機床