摘　要：針對由離散刀位點數據（jù）生成的五軸加工等距非（fēi）均勻有理（lǐ）Ｂ樣條曲線刀具路徑中兩條非均勻有理Ｂ樣條曲線參數不（bú）同步的問題（tí），建立了一種等距雙非均勻有理Ｂ樣條曲線參數的同步模（mó）型，實現等距雙非均勻有理Ｂ樣條曲（qǔ）線刀（dāo）具路徑插補過程中兩條非均勻有理Ｂ樣條曲（qǔ）線參數的同步運動。將（jiāng）三軸非均勻有理Ｂ樣條（tiáo）曲線插補算法應用於五軸加工等距雙非均勻有理Ｂ樣條曲線刀具路（lù）徑中的刀具中心點非均勻有理Ｂ樣條曲線，根據參數同步模型將插補算法同步到刀軸點非均勻有理Ｂ樣條曲線（xiàn）中。仿真表明，采用該算（suàn）法能夠使刀具始終沿著（zhe）等距雙非均勻有理Ｂ樣條（tiáo）曲線刀（dāo）路進行同（tóng）步插（chā）補，參數同步插補精度主要（yào）集中（zhōng）在１０－６　ｍｍ級數上，適用於複雜曲（qǔ）麵的五軸加工。

       關鍵詞：五軸加工；等距雙非均（jun1）勻有理Ｂ樣條曲線；參數同步；插（chā）補算法

       ０　引言

      隨（suí）著航空航天、國防、運載工具、動（dòng）力、裝備（bèi）等行業（yè）的飛速發展，由裁剪曲麵、組合曲麵和流行網格等複雜曲麵構成的薄壁零件被廣（guǎng）泛應用，如螺旋（xuán）槳、整體葉輪以及汽車（chē）覆蓋件精密模具等。五軸加工以其（qí）高速高精度的特點被廣泛應用（yòng）於該類自（zì）由曲麵零件加工［１］。五軸加工刀具軌跡是影響加工效率和加工（gōng）質量的重要因素，並直（zhí）接影響刀具壽命和機床損耗（hào）［２］，複雜曲麵的（de）零件（jiàn）通常對（duì）精度要求高、加工工藝性差，在（zài）切削力等（děng）因素的作用下，容易發生加工變形和（hé）切削振動。因此，獲得高質量的刀具路徑不但（dàn）可以提高加工過程的平穩性、減少機床頻繁加減速從（cóng）而提高整個加工的切削效率，縮短加（jiā）工時間，而且可以大大提高曲（qǔ）麵的加工精度及（jí）光順性、減少後續工序的工（gōng）作量。

      為獲得高品質的五軸加工刀具路徑，近些年來許多國（guó）內外學者對五軸（zhóu）加（jiā）工雙非均勻有理Ｂ樣條曲線（Ｎｏｎ－Ｕｎｉｆｏｒｍ　Ｒａｔｉｏｎａｌ　Ｂ－Ｓｐｌｉｎｅ　ｃｕｒｖｅ，ＮＵＲＢＳ）刀具路徑的規（guī）劃進行了深入研究。Ｌａｎｇｅｒｏｎ等［３］提出了分別對刀具中心點和刀軸點進行ＮＵＲＢＳ來擬合獲取雙ＮＵＲＢＳ曲線刀具路徑的方法，但（dàn）使用（yòng）所提方法生成的雙ＮＵＲＢＳ刀路（lù）並不等距。通過等（děng）距雙ＮＵＲＢＳ刀路（lù）能夠確定唯（wéi）一的刀具姿態，因而能獲得更加光順且精度更高的加（jiā）工路徑，實現高速平（píng）滑加工。基於此，Ｂｉ等［４］提（tí）出一種等距雙ＮＵＲＢＳ路徑的生成算法，利用四元數來描述刀具運動，分別擬合生成（chéng）雙ＮＵＲＢＳ刀路。Ｙｕｅｎ等［５］通過計算機輔助製造（Ｃｏｍｐｕｔｅｒ　Ａｉｄｅｄ　Ｍａｎｕｆａｃｔｕｒｉｎｇ，ＣＡＭ）係統獲得刀具中心（xīn）點和刀（dāo）軸矢量數據，將（jiāng）其分別擬（nǐ）合成五次（cì）樣條曲線，然（rán）後將各樣條曲線重新參數化，以獲得足夠（gòu）光順的樣條曲線刀具路徑。楊堂勇（yǒng）等［６］針對等距雙（shuāng）ＮＵＲＢＳ刀具路徑中不滿足精度的特（tè）點，給出了一種對偶四元數Ｂｅｚｉｅｒ矢量函數的光（guāng）順方法。通過研究發現，先前的生成雙（shuāng）ＮＵＲＢＳ刀路的方法中，在生成刀具中心點和刀軸點曲線時都使用了同一個參數ｕ。由於生（shēng）成兩條曲線的離散數據點不同，由累積弦長參數化等參數化方法得到的兩組節點向量勢必不同，如果使（shǐ）用同一個節點向量進行擬合，則（zé）將導致另一條曲線的擬合精度下降，從而降低刀（dāo）具路徑插補的精度。因此，為了獲得更高的加工精（jīng）度，在擬合雙ＮＵＲＢＳ曲線時應使用不同參數（shù）。

      本文（wén）針（zhēn）對刀具（jù）中心點的曲線參數和刀軸點的曲線參數不相同這（zhè）一特點，構建了一個雙ＮＵＲＢＳ曲線參數同（tóng）步模型，使得給出任意一個刀具（jù）中心點曲線的參（cān）數值（zhí）都能得出刀軸點曲線的參（cān）數值，以解決刀具中心點曲線和刀軸點（diǎn）曲線的參數同步問題，並應（yīng）用該模型實現等距雙（shuāng）ＮＵＲＢＳ刀具路徑的（de）同步插補。

     １　、五軸等（děng）距雙ＮＵＲＢＳ刀具路徑生成

     不同於三軸加工刀具（jù）路徑，五軸加工的刀具（jù）路徑不僅包含刀具中心點，還包含刀軸矢量信息。五軸等距雙ＮＵＲＢＳ刀具路徑中的一條為刀具中心點ＮＵＲＢＳ曲線，另一條為刀軸（zhóu）上某點的ＮＵＲＢＳ曲線，如圖１所示。任意（yì）時刻，通過對應（yīng）的刀具中心點與刀軸點即可確定刀軸矢量。

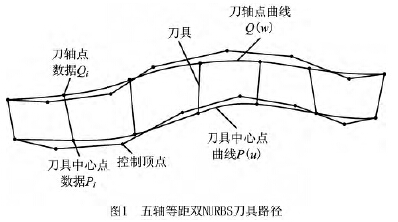
     將有序的離散刀位（wèi）點數據進行ＮＵＲＢＳ曲線插（chā）值，其主（zhǔ）要目的是求節點矢量和（hé）控製頂（dǐng）點。為簡化運算，將權重ωｉ賦值為１，此時ＮＵＲＢＳ曲線可（kě）簡化為Ｂ樣條曲線（xiàn）計算。由於高次插值（zhí）曲線（xiàn）存在難以給出的邊界條件，實踐中廣泛采用Ｃ２ 連續的三次Ｂ樣條曲線作為插（chā）值曲線［７］。

   
     １．１　刀具中心（xīn）點ＮＵＲＢＳ曲線的生（shēng）成

      三次Ｂ樣條（tiáo）曲線（xiàn）可定義為：

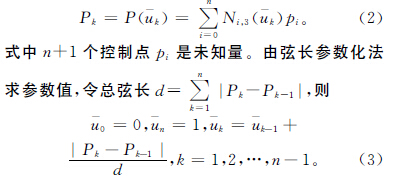
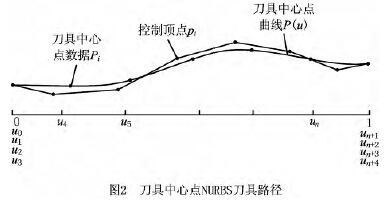
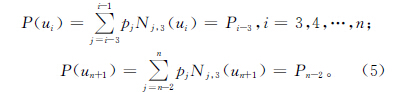
      式中含ｎ－１個方程與ｎ＋１個未知（zhī）頂點。對於Ｃ２連續的三次Ｂ樣條閉（bì）曲（qǔ）線，因具（jù）有（yǒu）周期（qī）性，首末數據點相重，不計重複，方（fāng）程數減少一個。ｎ＋１個頂（dǐng）點中的首末三個依次相重：ｐ０＝ｐｎ，ｐ１＝ｐｎ＋１，ｐ２＝ｐｎ＋２，未知（zhī）數頂點減少到ｎ－２個。因此（cǐ），可從ｎ－２個方程中求（qiú）解出ｎ－２個未知頂點。上述方程組可寫成下列矩陣形式：

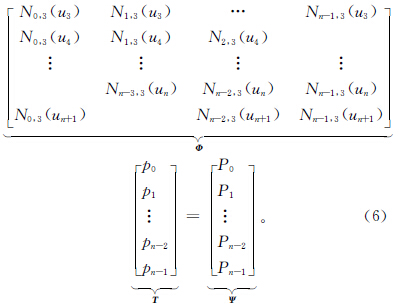
　    刀軸點ＮＵＲＢＳ曲線的（de）生（shēng）成

      圖３為刀軸點的刀具（jù）路徑示（shì）意圖，給定的（de）離（lí）散刀位點數據（jù）為一係列刀具（jù）中心點數據Ｐｉ和刀（dāo）軸矢量數據Ｏｉ，已知刀具為剛（gāng）體，則刀具上某（mǒu）點到刀具中心點的距離Ｈ 是一定的，因此刀具（jù）上某點的數據可（kě）以表（biǎo）示為

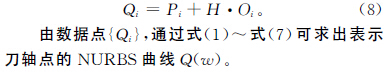
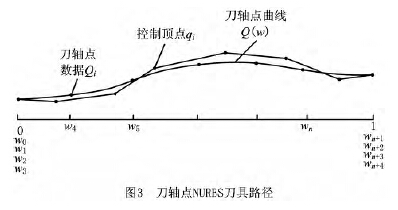
      ２　、等距雙ＮＵＲＢＳ曲線參數關（guān）係模型

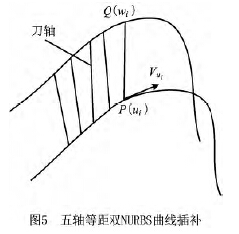
      五（wǔ）軸（zhóu）加工時刀具的運動不僅要保（bǎo）證刀具中（zhōng）心點的速度平滑，還要保證（zhèng）刀（dāo）軸矢量（liàng）轉動的速度平滑，而刀軸矢量轉動的（de）速度平滑可以通過刀軸上某點的速度平滑來保證。等距雙ＮＵＲＢＳ刀具路徑中刀（dāo）具中心點與刀軸點（diǎn）的（de）距離為一固定值Ｈ，分析（xī）五軸聯動雙ＮＵＲＢＳ 刀具運動軌（guǐ）跡可知（zhī），刀具中心點ＮＵＲＢＳ曲線Ｐ（ｕ）與（yǔ）刀軸點ＮＵＲＢＳ曲線Ｑ（ｗ）是平行並列（liè）關係，對任（rèn）意時刻曲線Ｐ（ｕ）的參（cān）數值ｕ∈［ｕｋ，ｕｋ＋１］時，都有曲線Ｑ（ｗ）的參數值ｗ∈［ｗｋ，ｗｋ＋１］。為保證刀具沿兩條ＮＵＲＢＳ曲線同步平滑運動，推導出任一瞬時兩ＮＵＲＢＳ曲線之間的（de）關係，並建立兩ＮＵＲＢＳ曲線的參數關係模（mó）型，如圖４所（suǒ）示。

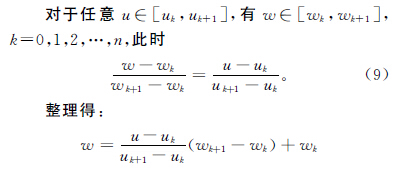
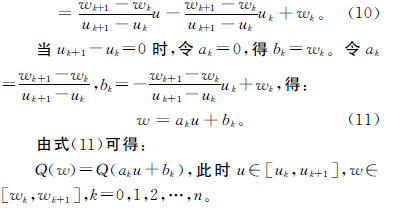
      在刀具中心點ＮＵＲＢＳ曲線（xiàn）Ｐ（ｕ）上任取一個參（cān）數（shù）值ｕ，都能在刀軸點曲線Ｑ（ｗ）上找到一（yī）個（gè）參數（shù）值ｗ＝ａｋｕ＋ｂｋ與之對應。

      ３　、五軸等（děng）距雙ＮＵＲＢＳ刀具路徑同步插補

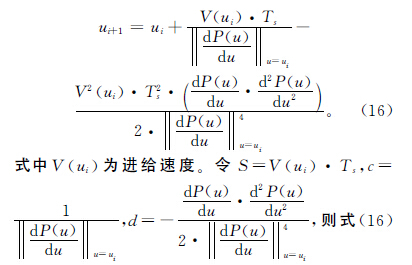
      不同（tóng）於三軸（zhóu）加工ＮＵＲＢＳ刀（dāo）具路（lù）徑的插補，五軸加工等距雙ＮＵＲＢＳ刀具路（lù）徑的插補不僅要（yào）考慮刀具中心（xīn）點的插補，還要考慮刀（dāo）軸矢量的插補，而刀（dāo）軸矢量的插補（bǔ）比（bǐ）較困難。本文先（xiān）求刀具中心點（diǎn）曲線Ｐ（ｕ）的（de）下一插補點參數（shù）值，再由兩ＮＵＲＢＳ曲線參數關係推導出刀軸點曲線（xiàn）Ｑ（ｗ）下（xià）一插補點的參數值。圖５所示為五軸等（děng）距雙ＮＵＲＢＳ曲（qǔ）線插補示（shì）意圖。

      由泰勒二階展開法，得刀具中心點曲線Ｐ（ｕ）下一插補點的參數值

       ４　、算例仿真

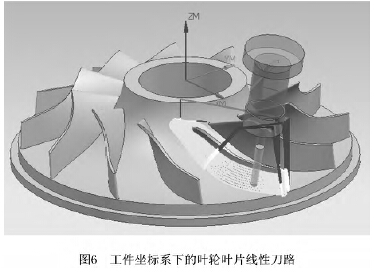
       本文采用基體高為９３ｍｍ、直徑（jìng）為３７２．６９ｍｍ的葉輪進（jìn）行仿真驗證，建模仿真如圖６所示（shì）。仿真算例驗證了本文所提同步插補算法的有（yǒu）效性，能（néng）夠對（duì）加工（gōng）葉輪葉片的線性刀路進行（háng）光順擬合，生成達到Ｇ１ 以上連續的等距雙ＮＵＲＢＳ刀具路徑，保證插補過程中的任意（yì）時刻（kè）均能保（bǎo）持（chí）等（děng）距，實現高速平滑加工。

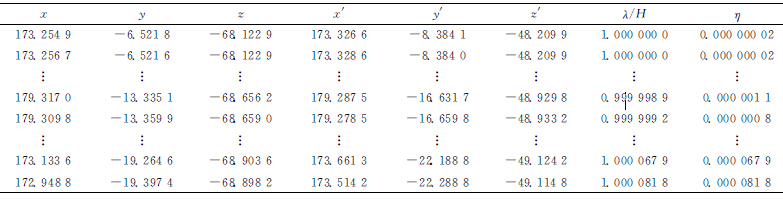
      由ＣＡＭ 加工模塊獲（huò）取工件坐（zuò）標下葉片模型的刀位點數據為一係列（liè）ＧＯＴＯ語（yǔ）句：

       其中，前三列為刀具中心點數據Ｐｉ，後三列為刀軸單位矢量數據Ｏｉ。由刀位點（diǎn）數據Ｐｉ和（hé）Ｏｉ，得到刀軸上某點的（de）數據Ｑｉ＝Ｐｉ＋Ｈ·Ｏｉ，設（shè）置（zhì）刀具中心點與（yǔ）刀軸點的距離Ｈ＝２０ｍｍ。將數據Ｐｉ和Ｏｉ分別進行三次ＮＵＲＢＳ插值，並采用文（wén）獻［９］給出的方法（fǎ）計算雙ＮＵＲＢＳ刀路的擬合誤差，以獲（huò）得滿足精度要求的兩條ＮＵＲＢＳ曲線Ｐ（ｕ）和Ｑ（ｗ），最後（hòu）對（duì）等距（jù）雙ＮＵＲＢＳ刀具路徑進行同步（bù）插補。為便於仿真計算，將ＮＵＲＢＳ曲線的權重ωｉ賦值為１，應用的插補算法是三軸ＮＵＲＢＳ插補中常用的泰勒二階展開法。

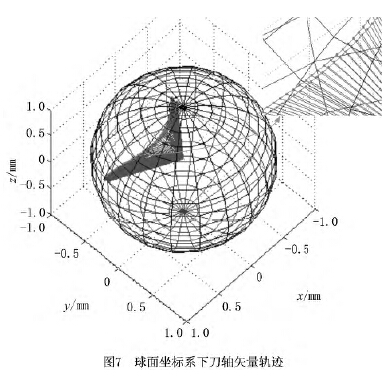
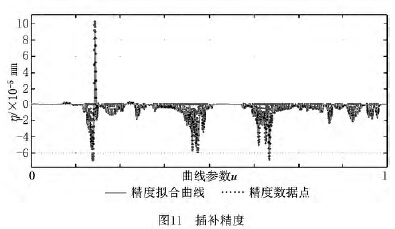
      由ＭＡＴＬＡＢ進行（háng）仿真驗證可（kě）得圖７～圖１０，圖７為球麵坐標係（xì）下刀（dāo）軸矢量軌跡（jì）的仿真圖，如圖可見刀軸矢（shǐ）量光滑地分布在球麵上，表（biǎo）明擬合光順性較好；圖（tú）８是在ＭＡＴＬＡＢ軟件下插值生成的五軸加工等距雙ＮＵＲＢＳ刀具路徑仿真圖，圖中的兩（liǎng）條ＮＵＲＢＳ曲線的任意對應點的間距都是（shì）Ｈ ＝２０ｍｍ；圖９為五軸等距雙ＮＵＲＢＳ刀具路徑的運行軌（guǐ）跡仿真圖，直觀地展現了刀（dāo）具任意時（shí）刻的位置和姿態；圖１０為等距雙ＮＵＲＢＳ插補圖（tú），由圖８插補仿真（zhēn）而來。

      設（shè）（ｘ，ｙ，ｚ）為刀具中心點ＮＵＲＢＳ曲線上的插補點，（ｘ′，ｙ′，ｚ′）為對應的刀軸點ＮＵＲＢＳ曲線（xiàn）上的插補點，      ，則λ表示兩點間的距離，η 表示刀軸矢量偏移量即插補精度。表１給出了部分等距（jù）雙ＮＵＲＢＳ刀具路徑的插補數據，λ／Ｈ 為兩條ＮＵＲＢＳ曲線上的插補點間距的（de）模，η＝λ／Ｈ－１為插補精度。如圖１１的插補精度中，數（shù）據點表示插補精度（dù）η，精度曲線由η擬合得到（dào），表示插補精度的大小。從圖１１可以看（kàn）出，插補精（jīng）度η 的值在１０－５　ｍｍ 的級數以下且主要集中（zhōng）在１０－６　ｍｍ的級數上，算法（fǎ）的插補精度較高（gāo），表明采用本文算法能夠（gòu）使刀具始終沿著等距的雙ＮＵＲＢＳ刀路進行同（tóng）步插補，能獲得更加光順（shùn）且精度更高的加工路（lù）徑，從（cóng）而使零件表麵的加工（gōng）質量更好。

 
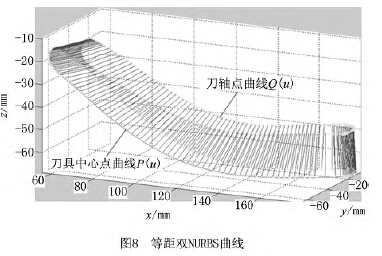
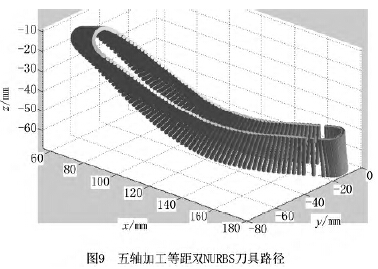
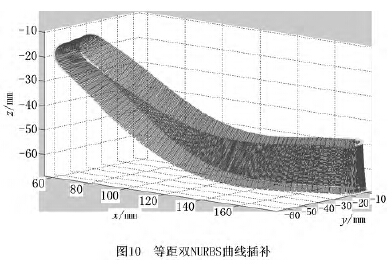
表１　等距雙ＮＵＲＢＳ刀（dāo）具路徑插補數據

       ５　、結束語

       本（běn）文提（tí）出一種（zhǒng）構建等距（jù）雙ＮＵＲＢＳ曲線參數同（tóng）步關係模（mó）型的算法，針對工件坐標係下的離散線性刀路（lù）進行光順（shùn），以（yǐ）獲取滿足給定精度且達到Ｇ１ 以上連續的等距雙ＮＵＲＢＳ刀具路徑，並實現高精（jīng）度的同（tóng）步插補。首先獲取刀位點數據並進行三次ＮＵＲＢＳ曲（qǔ）線插值，生成等距雙ＮＵＲＢＳ曲線刀具路徑；然後（hòu）分（fèn）析五軸加工等距（jù）雙ＮＵＲＢＳ刀路（lù）運動（dòng）軌跡，推（tuī）出任一瞬時兩條ＮＵＲＢＳ曲線之間的關係，並建立兩條ＮＵＲＢＳ曲（qǔ）線參數同步關係模型；最後根據三軸ＮＵＲＢＳ曲線插（chā）補算法求出刀具（jù）中（zhōng）心點曲線Ｐ（ｕ）下一插補點的參數值，並通過曲線參數關係推出對應的刀軸點曲線Ｑ（ｗ）下一插補點的參數值。仿真算（suàn）例表明（míng），所提算法可以生成等距雙ＮＵＲＢＳ刀（dāo）具路徑且參數同步插補模型精度在１０－５　ｍｍ級數以下並主要集中（zhōng）在１０－６　ｍｍ級數上。因此，算法（fǎ）的插補精度較高，適用於複雜曲麵的五（wǔ）軸加工中。本文的等距雙ＮＵＲＢＳ刀路同步插補算法，並未考慮機床運動（dòng）學與（yǔ）動力學等約（yuē）束。因此，可進一步研究機床運動學與動力學等約（yuē）束下的五軸聯動插補算法和機床各軸伺服能力約束下的進給速（sù）度、進給加速度的規劃問題。