基於EMD 分解在電火花數據分析的(de)應用
2017-1-9 來源:合肥工業大學電氣與(yǔ)自動化工程學院 作(zuò)者:劉春 杜雲(yún)
摘要: 經驗模(mó)態分解( empirical mode dccomposition,EMD) 是處理非平(píng)穩、非(fēi)線(xiàn)性信號一種有(yǒu)效的(de)新方法(fǎ)。運用EMD 分解法將(jiāng)脈衝典型負荷—電火花信號中(zhōng)本征模態函數( intrinsic mode function,IMF) 分量逐級(jí)分離出來,得到原信號的多尺度振蕩特性; 分析各個(gè)分量與原序列的顯著性檢驗和相關係數以及各個分量自身的周期性。用IMF 分量和趨勢項合成原序列並作誤差分析,得到信號的總(zǒng)誤差率通過理論計(jì)算為4. 3%。利用bior4. 4 和db2 兩種小波基在3 層分解係數(shù)基礎上對(duì)電火花數(shù)據展開小波包變換。最後借助MATLAB 平台對EMD 和(hé)小波包分解方法進(jìn)行仿真並做理論對比分(fèn)析。結果(guǒ)表明,EMD 分解法在提取機床運行放電特(tè)性及不同工況下信號更具優越性和有效性,提取結果更能滿足實際工程應用需求。
關鍵詞: 脈衝電能; 電火花(huā); 經驗模態分解; 小波包變換
1.引言(yán)
近幾年,采用電火花加(jiā)工技術在加工複雜型麵、深槽和窄縫等應用中(zhōng)所占(zhàn)比重越來越大(dà)。脈衝電能負荷不同的工況應用條件,造成脈衝電能質量擾動(dòng)因素種類繁多。放電狀態又(yòu)是對電火花加工過程實施(shī)準確控製的主要依據,直接決定了加工質量、加工效(xiào)率(lǜ)和電極損耗等工藝指標(biāo)的優劣[1]。然而,傳統電火花加工工藝效果受多種工藝參數( 尤其是電參數) 影響,加工工藝效果難以實(shí)現自動化生產。因此,研究電火(huǒ)花加工電參數的優化選擇,對工藝效果控製及自動化加工的實現具有重要意義[2]。從而(ér),進一步提高加工效率、精度及加工過程的穩定性(xìng)。
為了更(gèng)好地提高電火花加(jiā)工(gōng)表麵質量,國內外(wài)學者對其加工(gōng)表麵微觀形貌(mào)做了大量的研究(jiū)。研究比較多的有高斯濾波和小波(bō)濾波(bō)。Raja 等人(rén)[3]將快速傅立葉變換引入高斯濾(lǜ)波。Hara 等人[4]用兩階Butterworth 高通濾波器模擬高斯濾波的轉換(huàn)特性,提高(gāo)了運算速度卻導致了相移,降低了運算精度。但是,傅裏葉變換由(yóu)於信號的複雜性導致頻率(lǜ)變化劇烈,且它的窗口的大小固定不變,導致分(fèn)辨率固定。針(zhēn)對該缺陷,陳慶虎等人[5] 選擇Shannon 小波(bō),采用Mallat 快速分解算法,提出基於小波分析的理(lǐ)論和(hé)方法,小波濾波產生的三維基(jī)準麵,光滑自然,能(néng)精(jīng)確地把表麵粗糙度和其他表麵結構成份分(fèn)離。小波變換(huàn)繼承了窗口變換的局部化思想並改進了傅裏葉變換(huàn)的弊端,是一種自適應的(de)時頻分析方法; 但是小波變換在小波基選擇、小波(bō)基函數固定、閥值確定對於不同信號很難做出最佳選擇。為徹底解決傳統分析方法對電火花信號的的局限性[6-8],將不需(xū)要信號先驗知識(shí)和無需定義基函數的經驗模態分解( EMD) 法引入到電火(huǒ)花信號分析中(zhōng),把電火花信號內在的放電特性通過本征模態(tài)函(hán)數( IMF) 分量展現出來。
本(běn)文運用EMD 分解法對(duì)機床放電特性的電火花數據進行逐級分解,並綜合已有的小波分析方(fāng)法作對比,重點(diǎn)分析了(le)IMF 分(fèn)量與原數據顯著性檢驗和相關係數,采(cǎi)用自相關函數求功率譜尋找每個分量周期值; 將IMF 分量和趨勢分量逆變(biàn)換疊加還原(yuán)數據,對比原數據做誤差分析並考(kǎo)量原序列的主成分。本文最後部分,將實測電火花的電流信號分段做EMD 生產實際分析。EMD 分解法是分(fèn)析電火(huǒ)花機床的一種有效方法,IMF 分量(liàng)可體現電(diàn)火花機床的內在多尺度振蕩(dàng)特性(xìng)—放電特性,為電火花機床的運行狀態進行實時監控提供指導。
2.理論(lùn)基礎
2.1 IMF
EMD 將原序列分解成有限個IMF 分量,並且分量的瞬時頻率各不相同; 使得IMF 分量有物理意義的必要定義是: 函(hán)數關於零均值線是局部對稱,並且(qiě)穿零點和極(jí)值點的數目是一樣的。鑒於此,給出本征模(mó)態函數的確切定義: 1) 在信號序列裏,極值點的數目與穿零點的數(shù)目必須相等或者(zhě)最多相差一個; 2) 由局部極大值所構成的包絡線以及由局部極小值所構成的包絡線的平均值為零。對於非平穩信號而言(yán),定義一要對“局部平均”一段一段求,然(rán)而局部時間長度很難知道; 定義二是一個新思路,用上下包絡(luò)線的局部(bù)平均值為零來表征局部對稱性,巧妙的避開了局部時間尺度的問題(tí)。
ZMF 表征了信號序列內(nèi)在的,固有(yǒu)的振蕩狀態; “狀態”一詞,泛指漲落、起伏、變化,不一定具有周期(qī)性; 但(dàn)是如果一個振(zhèn)蕩經(jīng)過顯著性檢驗具有周(zhōu)期性,則稱之為周(zhōu)期性振蕩。
2.2 經驗模態函數分量IMF 的篩選過程
EMD 的關鍵性問題就是如何把一個非平穩非線性的信號分解成有限個IMF 分量和一個趨勢項。采用合適的篩選方(fāng)法,篩選出符合定義的IMF分量[9-11]。給定原信號,把所有(yǒu)局部極大值用(yòng)3 階樣條曲線連接起來(lái)得到上包絡線,運用同樣方法把局部極(jí)小值連接起來得到下包絡線; 上下包(bāo)絡線分別涵蓋信號全部極(jí)大值和極小值; 再取上下包絡線的均值(zhí)線m1,將原序列 X( t) 與均值(zhí)線 m1 ( t) 做差得到:
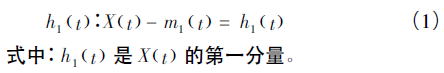
上述步驟隻(zhī)是篩選過程(chéng)的第1 步,得(dé)到的(de)h1 ( t) 不符(fú)合對 IMF 的要求,原因是: 1) 經 3 次樣條連接後把某些極大值誇大了,出現了一些(xiē)過(guò)高峰和過低(dī)穀; 2) 信號複(fù)雜,在峰或穀上有很多(duō)騎行波,就是零均值線的上下方起伏的彎曲,騎行波不滿足IMF 要求且一次篩選不能完全消除騎行波;3) 非線性信號來(lái)說,包絡的均值線和真正的局部平均線不一樣,某些非對稱波形依(yī)然存在,一次篩選無法消除非對稱波形。鑒(jiàn)於上述原因,必須進行重複多次篩選。
進行第2 次(cì)篩選時,把h1 ( t) 當作“原始序列”,重複第1 篩選步(bù)驟h1 ( t) - m11 ( t) = h11 ( t) ,

SD 的門限值要根據具(jù)體的信號來設定,門限的參考數值可取0. 2 ~ 0. 3。前後2 次篩選結果(guǒ)的SD 值達到預先設定值,則停(tíng)止篩選過(guò)程。第1 步篩選結果得到的C1應是信號的(de)特征時間尺度(dù)最(zuì)小的高頻IMF 分量。接下來,就把C1從原序列中分離(lí)出去,得到一個剩餘序列r1 ( t) :

2.3 小波包理論及濾波算法過程
小波分析的思想是用一簇函數去(qù)表示或逼近信號,這簇函數稱為小波函數係。在小波包分解過程中,隨(suí)分解層數增加數據點成倍減(jiǎn)半[12]。若電火花數(shù)據長度為2N ( 本文實(shí)測的電火花數據長度N = 10 ) ,分解L 次,則每(měi)個頻段數(shù)據長度變為2N - L。利用小波包可以將信號按任意時頻分辨率分解,將信號正交(jiāo)分解到相應的頻段。並根據先驗(yàn)知識,保留分(fèn)解序列中任意一個(gè)或幾(jǐ)個頻段序列進行重構,重構信號長度仍(réng)為2N。小波包濾波算法的實現過程:



3.仿真(zhēn)結果及(jí)分析
本文以一組實測機床放電電流全(quán)過(guò)程(chéng)電火花信號作為擾動信號樣本進行EMD 分解(jiě),得到5 個IMF 分量和一起(qǐ)趨(qū)勢分量R 如圖1 所示。根據實際經驗門限值通常去0. 2 ~ 0. 3。本次實(shí)驗的EMD門限值取0. 2。
3.1 IMF 分量的周期性分析
為了分析(xī)IMF 分量的周(zhōu)期性特征,本(běn)文采用基於自相(xiàng)關函數法(fǎ)求本征模態函數的(de)功率譜進而尋找周期性[13-14]。在MATLAB 中對(duì)各個分量進行(háng)功率譜分析,將獲得的最大(dà)譜對應的(de)周期如(rú)表1所示。

圖1 本征模態(tài)函數( IMF 分量和趨勢分量)
表1 自相關函數求功率譜尋找電流時間序列(liè)周期(qī)
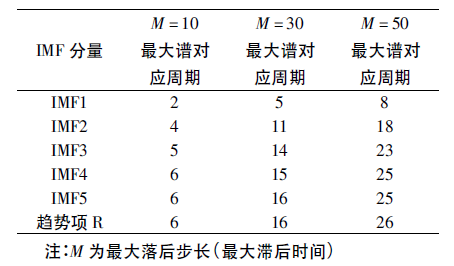
表(biǎo)1 結果(guǒ)表明: 本組數據EMD 分解後的每個細致分(fèn)量IMF 都(dōu)表現(xiàn)出一定的周期性。在最大落(luò)後步長M = 10,30,50 不(bú)同情況下,IMF 分量表現出不同的周期性,這是因為最大(dà)落後步長越(yuè)小導致時間序列越短,因而在基於自相關函數的功率譜(pǔ)最大譜上麵對應的周(zhōu)期越小; 但在低頻分量IMF4 和IMF5,對於最大落後步長對(duì)其周期性的影響減弱。深入分析IMF2 和IMF3 分量周期在不同M 值(zhí)的情況下周期跳躍(yuè)性(xìng)較大,結合圖1 中IMF2 和IMF3的幅值是其餘分量的10 和100 倍,假定IMF2 和IMF3 可(kě)能是原始信號的主成(chéng)分。
3.2 IMF 分量的顯著性和相關係數分析
為了更加準確地表征(zhēng)每個IMF 分量與原電流序列統有無(wú)顯著性差別和相關性程度[15],在MATLAB 中對每(měi)個分量進行顯著性檢驗和相關係數測定,結果(guǒ)如表2 所示。
表2 IMF 分量與原(yuán)電流時間序列(liè)的(de)顯著性檢驗和相關係數
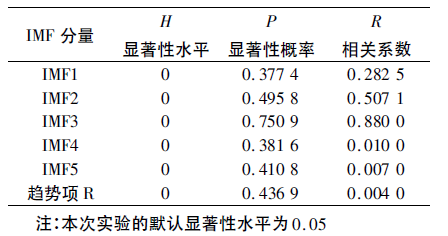
表2 結果表明: 在每個IMF 分量對原序(xù)列做顯著性檢驗時,發現顯著性水平H 值都為0,說明所(suǒ)有的IMF 分量(liàng)都(dōu)通(tōng)過了的顯著性檢(jiǎn)驗,結合上述的周期性分析,理論(lùn)上認為本組(zǔ)數據是周期性振蕩的。然而,每個分量的顯著(zhe)性概率卻不相同,表明每個分量(liàng)對於原序列的影響有(yǒu)大(dà)小之分(fèn); 結合相關係數的數據特點,有理(lǐ)由證實IMF2 和IMF3 是原序列的主成分,並且其攜帶了原信號大(dà)部(bù)分信息。
3.3 IMF 分量的逆變換和誤(wù)差(chà)分析


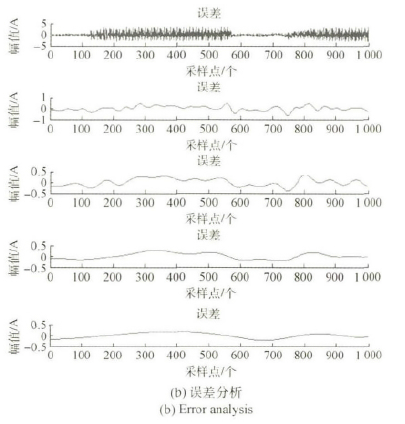
表3 誤差分(fèn)析
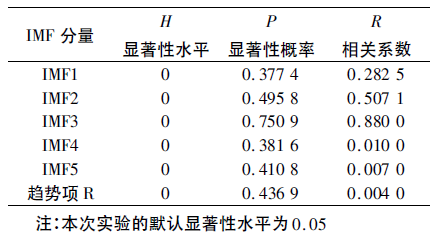
圖2 和表3 聯合結果表明(míng): IMF2 + IMF3 分量(liàng)雖然有(yǒu)誤差(chà)但在可接受範圍內,能較(jiào)好好擬合原電流時間序列,說明IMF2 和IMF3 是原(yuán)信號的主要分量,實驗(yàn)驗證了前(qián)麵理論分(fèn)析的正確(què)性。當(dāng)所有的IMF 分量相加後得到的信(xìn)號與原信號的總誤差率通過(guò)理論計算為4. 3%,說明EMD 分解法不(bú)僅可以表現信號的本質性質,同時不會減少信號的完備性; 也實現了EMD 分解法的逆變換。
4.應(yīng)用(yòng)分析
為(wéi)了更(gèng)清(qīng)晰地分析EMD 分解法的有效性,將同時利用小波分析和EMD 分解法對電火花數據進行分析。
4.1 小波包的電火花應用分析
以(yǐ)采樣時間為20 個工頻周期,采樣點N =1 000,采樣頻率fs = 1 kHz,取信號額定頻率為50 Hz。本文小波基函數分解是在3 層分解係數基礎(chǔ)上展開。利用MATLAB 的強大信(xìn)號處理功能,實現上(shàng)述過程,結果如圖3 和4 所示。
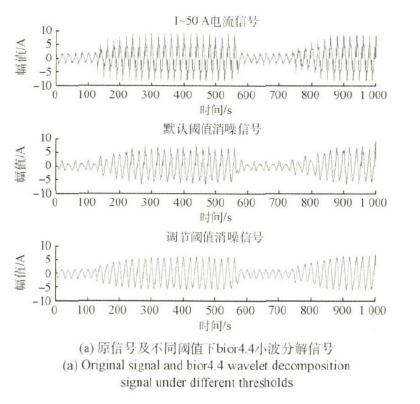
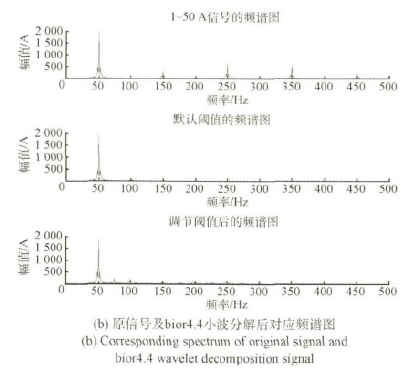
圖3 電火花50 A 信號bior4. 4 小波分解(jiě)
4.2 EMD 分(fèn)解的電火花應用分析
利用EMD 分解法(fǎ)對實測的機床電流放電過程進行分段分割分(fèn)析,並分析每(měi)個分量的頻譜特(tè)性,找到各分量的物理意義,從而更好地理(lǐ)解機床電流放電的內部過程。EMD 門限值取0. 2,利(lì)用MATLAB 繪製結果如圖5 和6 所示。
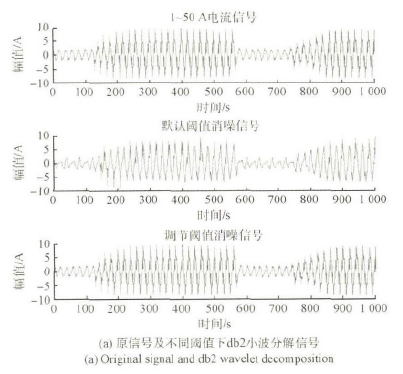
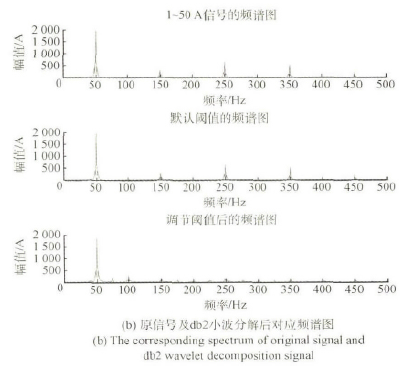
圖4 電火(huǒ)花50 A 信號db2 小波分解
4.3 小結
從圖3 和4 可以看到: db2 小(xiǎo)波在(zài)對(duì)電火花50A 信號的濾波效果不如bior4. 4 好,然而在(zài)頻率保持方麵db2 小波變現(xiàn)的更為出色。bior4. 4 小波(bō)在不同閥值對電火花去噪影響情況(kuàng)下,默認閥值的波形沒有調節閥值的好,而默認閥值的卻濾除了其餘諧波的影響(xiǎng)。圖5 和6 結果表明: 對於不同的機床運行過程,從IMF1 分量到IMF5 分量,都可以逐級清(qīng)晰(xī)地分解出原電流時間(jiān)序列不同階段的高頻和(hé)低頻分量。結合圖1 的趨勢項以及上一節的理論分析,可以看出經過(guò)EMD 分解後的電流序列個(gè)分量隨(suí)著時間變化(huà)呈現一些周期性(xìng)變(biàn)化。對(duì)於各分量(liàng)可以很容易看出: IMF1 包絡了信號的(de)5 次、7 次和9 次諧波含量,IMF2 包(bāo)絡了號的3 次、5 次和7 次諧波含量; IMF3 包絡了信(xìn)號的基波含量; IMF4 和IMF5 包絡了信號的低頻分量。
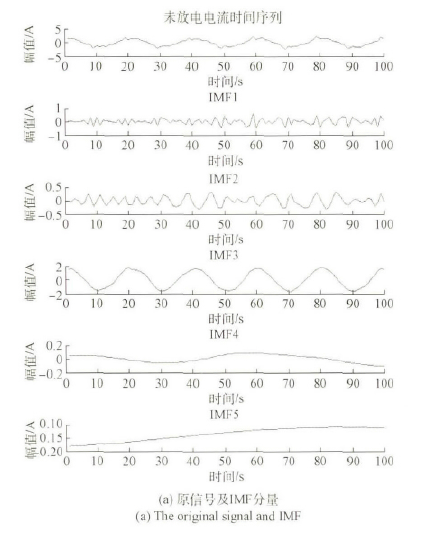

圖5 未放電電流時間序(xù)列EMD 分解和頻譜
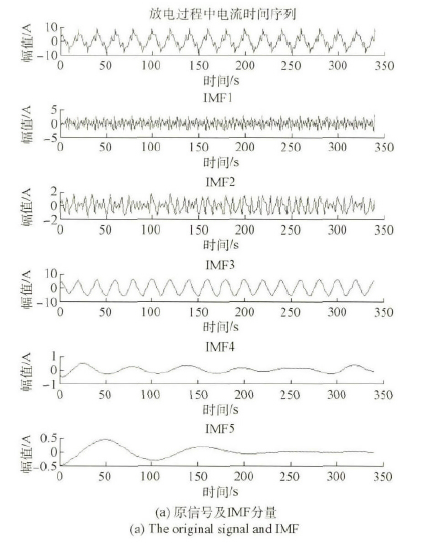

圖6 放電過程中電流時間序列EMD 分解和頻譜
對實測信號的試驗表明,采(cǎi)用需(xū)選擇合適的小波包算法,並給定合適的閾值才(cái)能(néng)分(fèn)析出點火花(huā)信號的部分特性。與小波分析法相比,一方(fāng)麵(miàn),EMD分解不(bú)僅無需(xū)信號的先驗知識(shí)和固(gù)定的基函數; 且可(kě)獲得電火花信號的內在放電特(tè)性。另一方麵,EMD 分解法在提取機床運(yùn)行的早期信號、微弱信號和突變(biàn)信號等各方麵信號更具優越性和高效性,提取(qǔ)結果(guǒ)更能滿足實際(jì)工程應用需求。
5.結論
EMD 分(fèn)解(jiě)法是一(yī)種新的(de)序列分解方法,本文以一組機床放(fàng)電電流特性(xìng)數據為基礎,借(jiè)助MATLAB 平台對EMD 分解過程和其分量進行細致的理論和實(shí)驗對比論證(zhèng),得出其在保(bǎo)證(zhèng)信號完備性的基礎上,具備處理(lǐ)間歇性、非平穩和非線性序列的良好效果,同時具有直(zhí)觀、簡潔(jié)和適應(yīng)性強等優點。因(yīn)此EMD 分(fèn)解方(fāng)法特別適用於電火花這類非平(píng)穩與非線性信號的處理給研究電火花加工(gōng)工藝參數和加工工藝效(xiào)果之(zhī)間的關係的研究人員提供了一種新思路(lù)。從而實現電火花加工向高效、高精、自動化(huà)方向發展。EMD 分解法剛剛起步,研究領域眾(zhòng)多,本文缺乏將EMD 分解法與經典信號分解法的對比性分析,將在以後的研究中改進。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資(zī)訊合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資(zī)訊合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息
業界(jiè)視點
| 更多
行業數據
| 更多
- 2024年11月 金屬切削機床產量數據
- 2024年11月 分地區金屬切削(xuē)機床產量數據
- 2024年11月 軸承出口情況
- 2024年11月 基本型乘用車(chē)(轎車)產(chǎn)量數據
- 2024年11月 新能源汽車產量數據
- 2024年11月 新能源汽車銷(xiāo)量情況
- 2024年10月 新(xīn)能源(yuán)汽車產量數據
- 2024年(nián)10月 軸承(chéng)出口情況
- 2024年10月 分地區金屬切削機床(chuáng)產量數據
- 2024年10月 金屬切削機床產量(liàng)數據
- 2024年9月 新能源汽車(chē)銷量情況
- 2024年8月 新能源汽車(chē)產量數據(jù)
- 2028年8月 基本型乘用車(轎車(chē))產量數據
博文選(xuǎn)萃
| 更多




