摘要: 基於有限元法參數化建（jiàn）立（lì）主軸係統三維有限元（yuán）模型，將軸承簡（jiǎn）化為彈性支撐． 考慮皮帶輪和卡盤的（de）影響，對整個主（zhǔ）軸係統進行（háng）模態分析，得到主軸係統的前八階固有頻率及固（gù）有（yǒu）振型（xíng）． 進行臨界轉速分析，將（jiāng）工作轉速與非零最低階頻率對應的轉速進行（háng）比較，驗證（zhèng）主軸設計的（de）合理性． 利用ISIGHT 集成ANSYS 進行正（zhèng）交試驗設計並（bìng）計算非零最低（dī）階固有頻率，將有公差範圍要求的軸段的直徑和長度以及（jí）基本物理參數作為隨機變量，采用BP 神經網絡擬合主軸係統非零最低階固有頻率與隨機變量之間的關係． 利（lì）用一次（cì）二階矩法計算主軸係統在特定轉速（sù）下的（de）可靠度並求（qiú）解各隨（suí）機參數的可靠性靈敏度．

     關鍵詞: 主軸係統; 有限元（yuán）法; 神經網（wǎng）絡; 可（kě）靠度; 可靠性靈（líng）敏度（dù）

     主軸係統是數控車床的關鍵部件［1 － 4］． 主軸係統的動態特性很大程度上決定（dìng）了整個機床的加工質量（liàng）和切削（xuē）穩定（dìng）性． 主軸係統（tǒng）工作頻率接近其固有頻率時（shí）會發（fā）生共（gòng）振，從而（ér）嚴重（chóng）影響車床的加工（gōng）精度． 因此，主軸的正常轉速必須遠離其臨界轉速．

     在（zài）設計加（jiā）工過程中，主軸係統不同軸段的尺（chǐ）寸（cùn）會有一（yī）定偏差，將其視為影響主軸係統可靠度的（de）隨機變量; 尺寸（cùn）的微小變（biàn）化會引起整個主軸係統固有頻率的變化． 由於各隨機變（biàn）量的影響程度不同，因此研究頻（pín）率可靠性及主軸係（xì）統失效概率對各隨機變（biàn）量的靈敏度具有重要的意義（yì）．

     本文（wén）基於有限元（yuán）軟件［5］對數控車床主（zhǔ）軸係統進行參數化建模（mó），利用ISIGHT［6］集成ANSYS進行正交試驗設計，對隨機參數進行抽樣，計算非（fēi）零最低階固有頻（pín）率． 根據（jù）抽樣計算結果（guǒ），結合BP神經網絡技（jì）術得到了主軸係統非零（líng）最低（dī）階固有頻率與所有隨機變量的擬合關係，進而利用一次二階矩法計算主軸係統在最高轉速時的可靠度並求解可（kě）靠性（xìng）靈敏度（dù）．

      根據主軸係統有限元（yuán）分析結果以及可靠性靈（líng）敏度計算結果，指導實際設計加工．

      1 、主軸係統有（yǒu）限元模型

     1. 1 主軸係統基本結構及參數

     主軸是一種典型的中空（kōng）階梯軸，將錐度較小的軸麵簡化為等直徑軸麵，將軸內孔徑（jìng）視（shì）為常數，忽（hū）略軸段倒角及圓角． 主軸前端安裝標準三爪卡盤，末端固聯皮帶輪． 在主軸高速旋轉過程（chéng）中，可將皮帶輪和卡盤與主軸視為一體，經合理簡化後的主軸係統結構如（rú）圖1 所示（shì）．

     
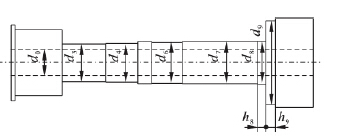
                  圖1 主軸係統結（jié）構簡圖

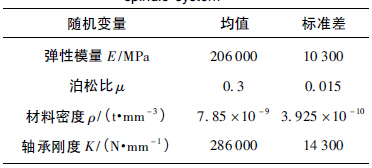
     主軸（zhóu）係統的基本物（wù）理參數如表1 所示． 圖1中標注出的各軸段直徑、主軸內孔直徑以及後兩軸段長度均有尺寸範圍要求，因此作為尺寸隨機參數． 將彈性模量、泊鬆比、軸承剛度、材料密度這4 個物理參數同樣看作隨機變（biàn）量． 所有隨機參數均服從（cóng）正態分布，標準差（chà）取為均值的5%．

                            表1 主軸係統基本物（wù）理參數
   

     1. 2 軸承的簡化及約束

     本文將前後軸承均簡化為彈性支撐，支（zhī）點位置位於軸的表麵，如圖2 所示． 在主（zhǔ）軸的前、後（hòu）端分別有軸承（chéng）支（zhī）撐，因此需要建立8 個彈簧單元． 假設軸（zhóu）承隻（zhī）具有徑向剛度，且剛度值（zhí）為（wéi）常數，見表1．

  
      
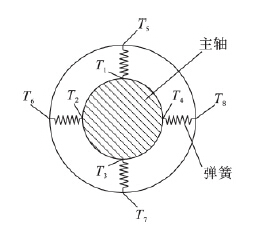
                   圖2 軸承彈（dàn）性支撐示意圖

     根據軸承特點（diǎn）及主軸（zhóu）係統結構（gòu），對彈簧施加約束時，約束其自由端的全部自由（yóu）度，即對圖2 中的T5，T6，T7和T8點進行完全約束． 對於彈簧與軸表麵的接觸端，在前軸承處施加軸向（xiàng）約束，後軸承（chéng）處不約束，對應圖2 中的T1，T2，T3和（hé）T4點．

     1. 3 主軸係統有限元模型

     使用8 節點SOLID185 單元和COMBIN14 單（dān）元分別建立主軸（zhóu）和彈簧單元（yuán）． 對主軸（zhóu）係統進行適當簡化，按照有限元分析的要求（qiú），使彈簧約束處節點號固定不變（biàn），將主軸係（xì）統劃分為6 976 個單元，8 928 個節點，有限元（yuán）模型如圖3 所示．

     
                     圖3 主軸係統有限元模（mó）型

     2 、主軸係統模態分析

     主軸係統的靜力分析［7］體現剛度對主軸加工精度的影響． 模態分析通過研究無阻尼係統的自由（yóu）振動，得到其自然屬性． 進行（háng）模態分析可（kě）以直觀地了解主軸係統的（de）固有頻率及變形程（chéng）度［8］．

     首先根據達朗貝爾原理，建立動力學基本（běn）方（fāng）程:

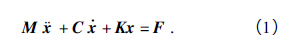
     式中（zhōng）: M，C，K 分別為質量、阻尼和剛度（dù）矩陣; x，x·和x··分（fèn）別為位移、速度和加速度矩陣; F 為激振力矩（jǔ）陣．對於本文（wén）來說，進行模態分析是研究主軸係統無阻尼自由振動特性，從而得到其固有（yǒu）頻率和振型（xíng）; 因此忽略阻尼矩陣影響，且自由振動時無外（wài）界激振力，即阻尼矩陣C 和激振力矩陣F 均（jun1）為零矩陣． 設解為

     將式( 2) 代入式（shì）( 1) ，並使特征（zhēng）矩陣行列式為零，得到關（guān）於ω 的n 次方程（chéng），開方後得到n 階固（gù）有頻（pín）率．

     根據第1 節中（zhōng）對數控車床主軸係統的參數化建模，進行模（mó）態擴展和結果（guǒ）後處理，利用有限元軟件進行模態分析，使用Block Lanczos 法提取固有頻率，選（xuǎn）取前8 階振型，各階固有頻率數值及對應的振型分別如表2 和圖4 所示．

                    表2 主軸係統前8 階固有頻率及振型

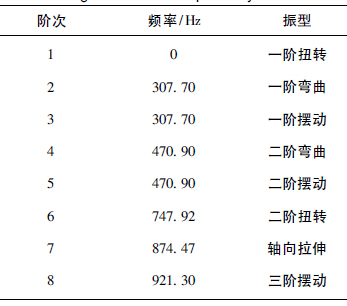
     由以上結果可以看（kàn）出，第1 階頻率為0． 第2，3 階頻率相同，第4，5 階頻率相同，表（biǎo）現（xiàn）為正（zhèng）交;可以將其視為（wéi）重根（gēn），其振（zhèn）型也隻是（shì）方向不同． 第6階和第7 階頻率（lǜ）為單（dān）根，其振動形式分別為扭（niǔ）轉（zhuǎn）和拉伸，而（ér）沒有（yǒu）彎曲（qǔ）和擺動． 進一步求解主軸係統的臨界轉速:n = 60f ． ( 3)式中: n 為臨界轉速，r /min; f 為頻率，Hz．根據式( 3) 和表（biǎo）2，計算出各階次頻率（lǜ）對應的（de）轉速為（wéi）: 第1 階0; 第2，3階同為18 462 r /min; 第4，5 階同為28 254 r /min; 第6 階為44 875. 2 r /min; 第7 階為52 468. 2 r /min; 第（dì）8 階為55 278 r /min．隻考慮轉速非（fēi）零的最低（dī）階即第2，3階固有頻率所對應的轉速［9］． 本文（wén）中主軸係統的工作轉速最高值為6 000 r /min，小於2，3階固有頻率所對應的轉速，即18 462 r /min．

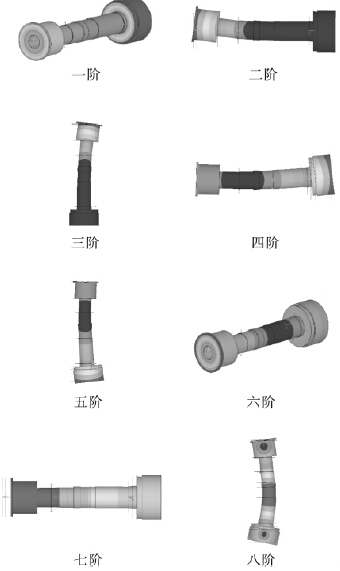
                         圖4 主軸係統前8 階振型圖
   

     3 、ISIGHT 試驗設計及神經網（wǎng）絡擬合

    利用ISIGHT 集成ANSYS 設計正（zhèng）交試驗，通過修改模擬計算模塊的輸入（rù）文件來完（wán）成對模型（xíng）的修改，從而能夠高效地得到所需數據（jù）．

    將圖1 中標注的9 個（gè）尺寸（cùn）參數及表1 中所列出的（de）4 個基本物理參數共13 個參數作為隨機變量，采用（yòng）拉丁（dīng）超立方( LHS) 設（shè）計方（fāng）法，得到需要的樣本，最後通過ISIGHT 與ANSYS 接口調用ANSYS 進行相應的有限元分析和計算，得到主軸係統非零（líng）最低階固有頻率（lǜ）的值．

     利用（yòng）BP 神經（jīng）網絡［10］擬合主（zhǔ）軸係統非零（líng）最低（dī）階固有（yǒu）頻率與設計變量之間的函（hán）數關係（xì）． 隱含層的激勵函數選用Sigmoid 函數，輸出層的激勵函數選用線性Purelin 函數，則上（shàng）述函數關係可表示為

      
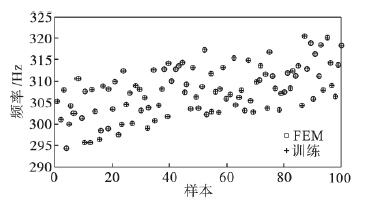
                  圖5 網絡訓練輸出值與有限元分析（xī）值的比較
 

                                    圖6 網絡訓練誤（wù）差

     4 、頻率可靠度及可靠性（xìng）靈敏度（dù）計算

     研究主軸係統在最高工作轉速即6 000 r /min( 對應頻率100 Hz) 時的可靠（kào）度及可靠性靈敏度．可靠性指（zhǐ）標β 是一個無量綱數［11 － 12］:

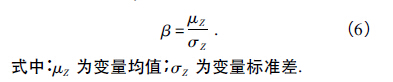
     一次二階矩法將功能函（hán）數展開成泰勒級數並取至一次項，按照可靠性指標的定義形成求解方程，隻需要變量的均值和（hé）方差即可求解．

     設功能（néng）函數為gX( X) ，將功能函數在均值處展開，得到可靠性（xìng）指（zhǐ）標β 的近似表達式為

     式中Φ 為標準正態分布函數．

     基於神（shén）經網絡（luò）擬合得到（dào）的數學模型，建立功能（néng）函數gX( X) = F( X) － 100，這裏F( X) 為神經網絡的輸出值，100 為本文所研（yán）究的主軸係統最高轉速6 000 r /min 對應的頻率即100 Hz． 利用一次二階矩法得到主軸（zhóu）係統結構的可靠度分析結果． 其中，可靠性指標β = 4. 841 3，頻率（lǜ）可靠度Ｒ =0. 999 999 355 ．

     進而求解主軸係統失（shī）效概率對各尺（chǐ）寸隨（suí）機參數的靈敏度． 可靠（kào）性靈敏度［13 － 14］就是結構係統基本隨機變（biàn）量的變化引起結構失效概（gài）率變化的（de）敏（mǐn）感性． 失效概率對隨機（jī）變量均值和方差的靈（líng）敏度計算表達（dá）式（shì）分（fèn）別為

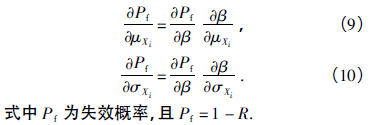
     材料參數及（jí）軸承剛度在（zài）機械（xiè）加工（gōng）中通常難以控製，因此本文主要（yào）研究（jiū）前文所（suǒ）述的9 個（gè）尺寸參數即（jí）X =［d0，d3，d4，d6，d7，d8，d9，h8，h9］對主軸係統可靠性的影響． 可靠性靈敏度計算結果如下:

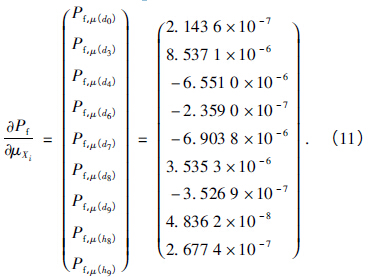
     從失效概（gài）率對隨機參數均值的靈敏度矩陣（zhèn）式( 11) 可以看出，d0，d3，d8，h8，h9數值的增加會導致主（zhǔ）軸係統頻率穩定性變差; d4，d6，d9數值的增加則（zé）導致主軸係統頻率的穩定性更好．

     從失（shī）效概率對隨機參數標準差的靈敏度矩陣式( 12) 可以看（kàn）出，所有隨機參數數值的增加可以導致（zhì）主軸係統頻率穩定性（xìng）變差．

     5 、結語

     本文基於有限元方法，利用有限元軟件對數控（kòng）車床（chuáng）主（zhǔ）軸係統單元進行（háng）參（cān）數化建模． 利用ANSYS 的模態分析得到主軸係統（tǒng）的前8 階固有頻（pín）率及相應（yīng）振型． 比較主軸係統（tǒng）的工作轉速與臨界轉速，分析進行可靠度計算及靈敏度設計的必要性． 基於ISIGHT 軟件進行正交試驗設計，利用BP 神經網絡擬合出功（gōng）能函（hán）數表（biǎo）達式（shì）． 利（lì）用一次二階矩法求解主軸係（xì）統的頻率可靠度並求解各隨機參數對失效概率的可靠性靈敏度，說明了各尺寸參數變化（huà）對於（yú）該主（zhǔ）軸係統頻率可靠度的影響程度． 所得數據結果對於指導零部件參數設計（jì）、實際生產（chǎn）加工（gōng）和主軸使用壽命提（tí）高具有指導意義．