摘要: 滾削（xuē）力產生機理複雜並具有時變（biàn）特性，是機床受迫振動（dòng）和顫振的重要因素，影響（xiǎng）齒輪加（jiā）工精度，但（dàn）滾齒加工原（yuán）理和刀具造型的（de）複雜性導致該問題一直（zhí）是切削力研（yán）究的難點，當前研究以實驗測量為主，理論分析較少。從實驗測試、理（lǐ）論計算和數值仿真這三（sān）個（gè）角度綜述了當今（jīn）滾齒切削力的研究進展，介紹了各自的主要（yào）研究方法、研究重點及已取得的成果，總結了（le）現階段（duàn）國內研究（jiū）存在的不足和尚需攻克的難點，為類似研究提供參（cān）考。
 
      關鍵詞: 滾削力; 測量; 理論分析（xī）; 仿真
   
      0 引言
 
     齒輪（lún）加工中，機床的動靜態特性對加（jiā）工質量有很大影響，滾齒產生的時變切削力是迫使機床振動的重要（yào）因素。對於高速、高（gāo）精的數控滾齒機而言，力、溫度等（děng）物理參數是自適應控製的重要依據［1］。切削力直接導致刀具磨損（sǔn）、崩刃以及摩擦生熱，嚴重影響（xiǎng）齒輪加工精度。切削力研究（jiū）有（yǒu）助於（yú）刀齒強度設計、切削過程優化、機（jī）床結構設計、製定（dìng）合理的工藝過程及切（qiē）削顫振分（fèn）析，是（shì）關乎切削穩定性和機床動態特性的重要因素，掌握（wò）滾削力的發生（shēng）機理對機床設計（jì）和切削控製意義重大，能更（gèng）好地發揮（huī）機床（chuáng）的切削性能，提高加工精度。
 
      到目前為止，眾多學者從實驗和理論角度測（cè）量、分析和計算了各種條件下的最大（dà）切削力和平均（jun1）切削（xuē）力，總結了影響滾削力的主要因素，取得了一定的（de）研究成果，但因滾刀造型、切削原（yuán）理和切削過程的複雜性以及昂貴的試驗費（fèi）用，使得實驗及理論計算存在一定（dìng）的誤差，尤其對於理論分析，建立起能完（wán）全估算各類工藝參數如（rú）切屑幾何、刀具磨損和滾削力的分析模型較困難，要完全考（kǎo）慮加工過程中的各種因（yīn）素更為困難。
 
      滾削力可沿工（gōng）件圓周徑向、切向和軸向分解為Fx、Fy和 Fz三個相互垂直的力，若忽（hū）略滾刀直徑因素，則上述（shù）分力也同時作用於（yú）刀杆上。實驗測量、理論計算和軟件仿真都是通過得出三向分力，繼（jì）而集成（chéng）得（dé）到總的滾削（xuē）力。滾削力的測量和理論研究基本（běn）處於同時發展，相互推進的現狀，研究人員根據大量的測量數據推導了一些經（jīng）驗公式; 在理論計算時（shí）需要實驗驗證計算結果的準確度（dù）。
 
      1 、滾削（xuē）力測量
 
      早期，多數學者（zhě）以實驗作為研究手段，測量結果的準確程度依據測量裝置本身的測量精度。設計合理的實驗裝置和係統（tǒng）是必要條件。測量對象可（kě）分為對飛刀和滾刀兩種切齒方式的測量，測量方法（fǎ）可分為在滾齒機上直接測量和以飛刀作為替代的間接測量，飛刀應用（yòng）較為靈活，在不具備滾齒機的條件下也可使用［2］。
 
       1． 1 硬件測量裝置
   
      不同於壓電測力儀［3］等測力裝置在（zài）其他金屬切削工（gōng）藝中的（de）廣泛應用，滾削（xuē）範成運動自身的複雜性導致高精度滾削力測試裝置的設（shè）計製造仍（réng）然較為困難［4］，多采用傳統的三向（xiàng）測力裝置，該裝置一般由應變式傳感器、動態應變儀和光線示波器組成（chéng），但該（gāi）裝置存在動態特（tè）性差、抗（kàng）幹擾能力弱及效率低的缺點，因此，為達到精確測量的目的，所設計的測（cè）力儀需滿足如下性能要求［1］。
 
      1) 具有足（zú）夠的靈敏度且能測出瞬態三向切削分（fèn）力的（de）變（biàn）化（huà）值，各切削分力之間（jiān）的相互幹（gàn）擾要小，讀數穩定，重複性小（xiǎo）。
      2) 具有足夠的（de）剛度（dù）和較高的自振頻率，保證（zhèng）測試數據（jù）的可靠性（xìng）。
      3) 切削力作用位（wèi）置點改變時，不 應 產 生 測 量誤差（chà）。
      4) 結構簡單，製造容易，裝配方便。
 
      1． 1． 1 接觸式測量裝置
   
     一般的滾削測（cè）力儀具有（yǒu）特製的刀具心軸和工件心軸，以此（cǐ）作為彈性元件，並在變形（xíng）敏感部位貼有（yǒu）電阻應變片以組成（chéng）橋式電路，切削力信號由集（jí）流環或遙感裝置輸出［5-6］，但這種測力儀通用性較差，一種滾刀（dāo）直徑隻能（néng）對應一種滾齒機，靈敏度受切（qiē）削力作用（yòng）點影響，集流環的使用增加了測量誤差（chà），設備的布置及安裝需在床身上打孔［7］，安裝極為不便。電阻應變片式測力儀使（shǐ）用廣泛［8-11］，變（biàn）形原件常見形式（shì）有直筋式、八角環式和薄壁筒式等（děng），直筋式（shì）在保證精度的前提下易於製造，應用較廣［1］，測試係統原理及流程圖分別如圖 1 和圖 2 所示（shì）。圖 1 和圖 2 中，Fx、Fy和 Fz分別為工件圓周徑向（xiàng）、切向和（hé）軸向滾削力，M 為切削力矩。
 

      1 、測試係統原理（lǐ）圖
 

      2 、滾削力采集流程圖
 
     除此之外，應變片與（yǔ）刀具一體式測量（liàng）儀也見諸報道。圖 3 所（suǒ）示為一種飛刀三向測力儀［9］，圖中 A、B、C皆為應變片，分別（bié）測量主分力 P1、橫向分力 P2和徑向力 P3，P 為總切削力。通（tōng）過（guò）檢測十字環的變形可測出三向（xiàng）分（fèn）力，在切（qiē）向（xiàng）進給機構的作用下，該裝置可沿徑向進給以實現整個齒槽的切削。此裝置安裝簡單方便（biàn）並可實現順銑和逆銑兩種方式的切削，但（dàn）製作較為（wéi）複雜。
 
     電阻應變片造價較（jiào）低，但測試靈敏（mǐn）度（dù）與其自身剛度相關。要精確測量切削力（lì），測（cè）力儀自身（shēn）剛度（dù）要高（gāo），必須使其固有頻率（lǜ） ωn 大於或等於切削（xuē）力激（jī）振頻率 ω，但剛度的升高又（yòu）會影響靈敏度，故需要綜合考慮切削（xuē）速度和測試係統自身的（de）各種因素（sù），以尋找兩者之間的平衡點。
 
     因（yīn）此，要（yào）克服電阻應變片測（cè）量裝置存在的上述缺點，精確測定滾削力，需要新型傳感器及微（wēi）機采樣（yàng）係統（tǒng）。
 

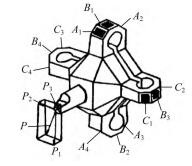
     圖 3 飛刀三向測力儀
 
     微機測（cè）試係統具有高（gāo）精度、高分辨率和較高靈敏（mǐn）度（dù），即使受到幹擾也能夠通過軟件補償［6］，圖 4 所示為一種查詢式滾削力微機測試係統框圖，從（cóng）圖 4 中可以看出，由滾齒測力儀應（yīng）變片（piàn）測（cè）得的電阻變化信（xìn）號依次經（jīng）過動態應（yīng）變儀（yí）、放大電路和 A /D 轉換器，最（zuì）終轉換為數（shù）字信號，由霍（huò）爾元件構成的控（kòng）製信號電路對此信號處理後即可以（yǐ）切削力圖的方式（shì）通過微機輸出，測試結果直觀易懂。
 
      4 、查（chá）詢式滾（gǔn）削力微機測試係統框圖
 
     圖 5 所示為滾（gǔn）削力微機測（cè）量係統，是一種更為複雜的測試裝置［12］，此係統能測（cè）量（liàng）並計算整個齒輪加（jiā）工過程中的滾（gǔn）削分力，計算機（jī）實時監測並管理所有測量設備，被（bèi）測的力信號由大容量存（cún）儲單元存儲並與計算結果進行比較，繼而（ér）通過（guò）顯示器顯示。
 

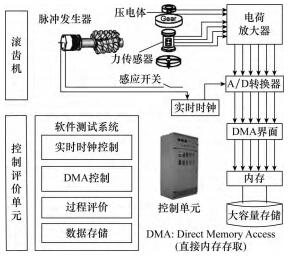
     圖 5 滾削力微機測量係統
 
     上述幾種測量裝置雖在精度上有所提高，但不易安裝，測量精度受應變（biàn）片粘附位置的影響，因（yīn）此需開發新的測量裝置。
 
     1． 1． 2 非（fēi）接觸式（shì）測量（liàng）裝置
 
     非接觸式測量裝置主要由無線遙測應變儀構成［4，13］，因應變儀對稱安裝並能隨著夾具旋轉，從而消除了質量不（bú）平衡引起的自激振動。
 
     圖 6 所示為一種無線遙測裝置的結構鋼工件夾具，三個壓電測力儀間距 120°沿底麵圓周排列，可在不改變（biàn）結（jié）構或幾何尺寸（cùn）的（de）前提下安裝在（zài）各類滾齒機（jī）上，並能隨工作台一（yī）起轉動。無線遙測裝置能實（shí）時檢測加工過（guò）程（chéng）中的切削力，最後通過電腦顯示。此外，紅（hóng）外成像儀也有應（yīng）用［2］，監測時將切削部位作為對焦點，即能在測量滾削力的同時監測切削熱。
  
  

    
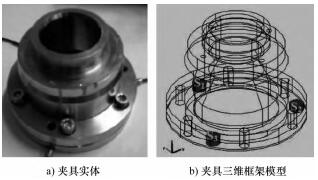
     圖 6 無線遙測裝置（zhì）的工（gōng）件夾具
 
     1． 2 實驗所得結論及（jí）影響因素
 
     大量滾削力測量實驗表明，滾削力為隨時間變化的交變力，滾（gǔn）刀（dāo）每一轉代表一個變化周期，一（yī）個周（zhōu）期內的波峰數（shù）與滾刀容屑槽數正相關。圖7 所示為平均滾削力在一個（gè）周期的變化過程，圖7 中顯示（shì）十個波峰，說明該滾刀有十排刀齒［14］; Umezaki 的研究表明: 主切削力（lì） 沿 工 件 軸 向 最 大，其他兩個方向切削力較小（xiǎo）［15］。除（chú）此之（zhī）外，切削參數、刀具幾何參數、切削工藝（yì）和工件材料等因素對滾削力的影響如下（xià）。
 
     1) 切削參數（shù）: 對同一種材料，滾削力隨切削（xuē）深度、垂直進給量、軸向進給量、齒輪螺旋角和齒輪齒數的增加而上升，隨切削速度的升（shēng）高而（ér）下降。
 
     2) 刀具參數: 滾（gǔn）削力隨刀（dāo）刃夾角減小而上升［16］;滾刀後角對滾削力影響比前（qián）角大（dà）; 正前角（jiǎo）和較大後角（jiǎo）刀（dāo）具的切削動態性能較好; 模數與力（lì）和力矩成正比;側刃比（bǐ）頂刃（rèn）的金屬切除率大，但頂刃因切（qiē）削次（cì）數少故受力（lì）比側刃大; 齒數( 齒輪、滾刀) 對（duì）切削力（lì）矩無影響。
 
    3) 切削（xuē）工藝: 幹切削比濕切削的滾削力大（dà），但若為高（gāo）速（sù）幹切，則切削力與低速幹切（qiē）相比又會降低; 逆滾時滾削力大於順滾，順滾時 X 向滾削分力 Fx 更大，Fz 較小，而 Fy 則在 0 周圍波動［17］，斜齒輪情況類似;滾削力矩和溫度也有類似的結論，因此采用高速（sù）滾齒技術有較多優點。
 
    4) 工 件（jiàn） 材 料: 對於（yú）硬齒麵（miàn）加工，在 HＲC36 ～HＲC46 範圍內，滾削力一般低於同材質軟（ruǎn）齒麵（miàn）滾削（xuē）力，但中（zhōng）硬齒（chǐ）麵的齒輪（lún）其滾（gǔn）削力（lì）梯度值遠大於軟齒麵滾削力（lì）梯度值，產生這一結果（guǒ）的原因可認為是齒麵硬度、強度的增加與塑性降低的（de）相互（hù）作用，若（ruò）後者起（qǐ）主導作用，則滾削力下降; 梯度值的升高歸因於加工硬齒麵時刀具所受的較大衝（chōng）擊。由此可見，滾切中硬（yìng）齒麵（miàn）齒輪時，由衝擊和振動帶（dài）來的動載荷問題不能忽略［18］。由以上分析（xī）可以看出，采用測（cè）力裝置能較為直觀地反映加工過程中的切削力大（dà）小（xiǎo），根據切（qiē）削力圖可實時調整切削速度（dù）、進給量等切削參數，避免由切削力引起的受迫振動及顫振，可提高（gāo）加工穩定性，還可整理出較為合適（shì）的切削數據庫，但操作過程繁瑣複雜，需（xū）要大量實驗，耗費大量人力、物力及財力; 而理論公式的欠缺也不利於進一（yī）步的研究。
 

     圖 7 平均滾削力變化
 
    2 、軟件仿真
 
     近年來有限元理論在金屬切削（xuē）領域應用廣泛，各種 軟 件 層 出 不 窮（qióng），如 AdvantEdge、DEFOＲM 3D、ABAQUS 等。部分學者利用上述軟件（jiàn）進行了滾齒切削力的研究［19］。因滾削運動較為特（tè）殊，而通用有限元軟件計算精度較低［20］，故研究人（rén）員開發了幾種基於通（tōng）用 CAD 平台的（de）嵌入式專用程序，依賴 CAD 軟件自身強大的計（jì）算能力可（kě）獲得更高的（de）計算精度，如HOB3D［21］、WZL SPAＲTApro［22］及基於 Matlab 的 FＲSDNY［20，23］。鑒於上述（shù）軟件所（suǒ）依賴的數學模型不同，可將軟件分為兩類: 1) 基於有限元方法（fǎ）的切削力計算軟件; 2) 基於切屑（xiè）幾何參數的（de）計算軟件。
 
     第一類軟件計算過程有大量的資料可供參（cān）考，不再贅述; 第二類軟件（jiàn）的操作過程具有相似（sì）性: 計算前要作前處理，需輸（shū）入加工所必須的參數如（rú）中心軸距、刀具與工件的幾何參數以及加（jiā）工環境條件。依 據（jù）Kienzle-Victor 模型並通過計算未變形切屑的各項參數，即（jí）可得各向（xiàng）分力。計算（suàn）時需知刀刃在每個（gè）切削層上（shàng）切屑的（de）幾何形態並將切屑垂直於切削刃離散，滾（gǔn）削分（fèn）力離散示意（yì）如圖 8 所（suǒ）示，可見切屑被離散為四邊形單元，以每個四（sì）邊形邊緣中點為著（zhe）力點進行分解，算出每個單元寬度 b 和高（gāo）度 h 之後便可計算相對應的切削分力。各（gè）項（xiàng）分（fèn）力分別用 Fr、Fs和 Fv表示，其中，Fr平行於（yú）切削刃，Fs與切削速度同向，Fv則（zé）分別與 Fr和 Fs相垂直，三者疊加可得總切削力。該模型（xíng）誤差主要來自於切屑麵寬（kuān）度的選擇，即實際麵積與等效四邊形麵積之差。另外此類軟件可實（shí）時模（mó）擬每個刀刃產生的切屑形態，以便觀察每個刀刃（rèn）的切削量。
  

    
  
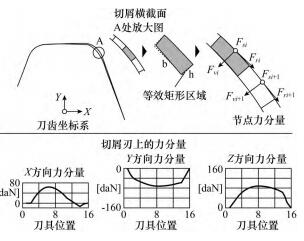
     8、 滾削分力離散示意
 
     圖 9 所示為切削（xuē）一個齒槽時切屑形態的變化情況［21］。因一個齒槽由多個滾刀刀齒（chǐ）切削而（ér）成，故不同切屑對應不同刀齒，為（wéi）便於區（qū）別（bié），將切（qiē）屑（xiè）刃按照數字進行編號: 當（dāng）刀齒（chǐ）滾過齒槽中心時，若刀（dāo）齒的局部坐標 Y1 平行於工件（jiàn）局（jú）部坐標 X2，則該刀齒被記為“0”;早於（yú）刀齒“0”通過工件中心（xīn）的記為“1”，反之則記為“－ 1”，以此例（lì）推（tuī）。可看出: 左、右兩側刃及頂刃的切削量各不相同。Nikolaos［21］研究得出: 切屑主要由頂刃（rèn）產 生，約 占 60% ，而兩個側刃僅僅參與齒形的形成。
  
  

   
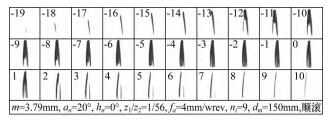
    圖 9 切（qiē）屑形態變化
 
    圖 10 所示為通用有限元軟件與 FＲSDYN 計（jì）算結果（guǒ）的比較。可見，雖然三條曲線在形狀上極（jí）為相似，但幅值相差甚大，有（yǒu）限元軟件計算結果明（míng）顯偏大。引起此偏差的原因可能為刀具（jù）和工件有限元（yuán）模型離散化程度過高，這（zhè）種偏差隻能靠（kào）提（tí）高建模精（jīng）度來（lái）彌補，但太高的（de）建模精度會消耗大量的計算時間（jiān）和硬件資源，並（bìng）不可取。由此可見，有限元算法距離實際應（yīng）用還有較大差距，而基於切屑橫（héng）截麵參數的專用滾削仿真程序則存在較高的實用價值，但專（zhuān）用程序也存在（zài）一定問題。圖 11 所示為 SPAＲTApro 計算的（de）滾削力矩（jǔ）與（yǔ）實際測量值的比較，可看出力矩的變化（huà）雖然在時間進程（chéng）上一致，但（dàn）幅值有一定差別，究其原因是計算程序中沒（méi）有考慮實際切削時的動態（tài）效應( 如切屑流動) 的影響。
  
  

   
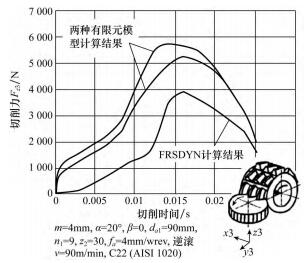
    圖（tú） 10 有限（xiàn）元軟件與 FＲSDYN 計算結果比較
  

   
  
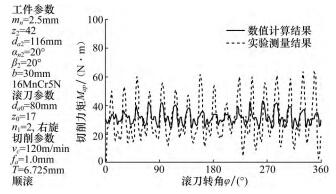
    圖 11 SPAＲTApro 計算結果（guǒ）與實際測量值比較
 
    3 、理論分析及計（jì）算
 
    理論分析主要在於（yú）對切削區域（yù）大小和形狀的確定、滾刀幾何形狀對切削力（lì）的影響和滾（gǔn）齒（chǐ）過程中的切屑變形規律的（de）研究［24-30］，前兩類主要基於實驗現象，所建立的模型較為簡單，大多隻考慮頂刃切削而忽略了側刃和（hé）切屑厚度的變化。因此，滾（gǔn）削力的理論分析大致基於兩種方法: 1) 基於實驗測量（liàng）的（de）經（jīng）驗公式; 2)考慮切屑幾何參數的（de）數學計算。
滾削力（lì）簡化模（mó）型可（kě）分為兩類: 齒條模型和飛刀模型［16，31-34］。滾刀造型的複雜性使（shǐ）得（dé）理論研究較為困（kùn）難，根據滾刀形成原（yuán）理和齒輪齧（niè）合（hé）原（yuán）理，滾刀（dāo）由蝸（wō）杆變化而（ér）來，且單頭滾刀與齒條共軛，因此多數研究以齒條作為研究對象［32，34］; 另外，滾刀刀齒形狀和切削原理也與飛刀近似，故大多對滾削力、切屑變形［23］、切（qiē）削溫度［35］和刀具磨損［36］等的研究都以飛刀為對象進行。
 
    3． 1 基於實驗測量的經驗公式
 
    根據大量（liàng）實驗結果數據擬合而成的公（gōng）式為經驗（yàn）公式，但因實驗條件的差異以及所考慮因（yīn）素的不同，滾削力公式形式多樣，往往為單參數公式［11］，如切削速度影響下（xià）的滾削力: F = 305． 8V － 0． 005［13］等（děng）。上述公式假定其他工藝參數不變，隻研究某一參數影響下的滾（gǔn）削力，雖可得出（chū）較合（hé）理的計算結（jié）果，但沒有考慮其他工（gōng）藝參數（shù）的（de）影響，普適性較差。除此之外多參數影響下的滾削（xuē）力公式也有不少，如:
  
    
  
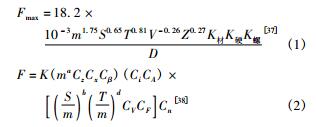
    式中: Fmax為最大滾削（xuē）力; m 為法向模數，mm; S 為軸向進給量，mm / s; T 為吃刀深度，mm，T = t /2． 25，其中 t為進刀深度; V 為切削速度（dù），m /min; Z 為工件齒數; K材為工件材料修正係數; K硬 為工件硬度修正係數; K螺 為螺旋角修正係數; D 為（wéi）滾刀外徑，mm; F 為主切削力（lì），N; m 為模數，mm; Z 為齒數; x 為位移量，mm; β 為螺旋
角，( °) ; i 為滾刀的排屑槽數; S 為走刀量，( mm /t·r) ; T 為切削深度（dù），mm; V 為切削速度（dù），m /min; F 為滾切方法; W 為齒輪材料; K 為常數（shù）; C 為係數; a、b、d 均為指數。
 
    上述兩式分別從不同角度衡量滾削力，但參（cān）數極多且需嚴格按照實際加工工藝確定，過程複雜（zá）; 因（yīn）此，要迅速精確地計算滾削力還需（xū）從切屑形成本質上進行（háng）分析。
 
    3． 2 考慮切屑變形幾何參數的理論計算
 
    與銑削力（lì）的三（sān）維模（mó）型類似［39］，滾（gǔn）削力理（lǐ）論計算的關（guān）鍵在於齒廓（kuò）生（shēng）成位置上未變形（xíng）切屑橫截麵積的確定，主要考慮兩個因素: 切屑寬度（dù）和厚度（dù）［40-41］。為確定切削力分量（liàng），需記錄在加工過程中單個（gè）刀齒的各旋轉位置上每個切屑（xiè）生成時前刀麵的各切削參數，即在（zài）切削區域內建立切削層，沿滾刀長度方向計算每（měi）一層切（qiē）屑的橫截麵（miàn）積。滾削單元分力確定如（rú）圖 12 所（suǒ）示，相對於刀齒的前刀麵參考係，在滾（gǔn）削的每個旋轉位置，前刀麵上的切削刃和切屑（xiè）被分（fèn）解成微（wēi）小單元［20］，作用在單元（yuán） i 上（shàng）的切削力（lì） Fi 會對該刀齒產生影響，此力可分解為 Fci和 Ffpi，如圖 12 右半部分車削模型所示（shì）。在計算得切屑寬度 bi和厚度 hi後，利用（yòng） Kienzle-Victor 模型的計算公式 Fi = Ki × b × h( 1 － Z)即可得出該切削分力，其中（zhōng） Ki為材料係數。圖 12 下半部（bù）分所（suǒ）示為滾刀齒上的切削力（lì）模型，其中符號 F、Fxi和 Fyi分（fèn）別與前述的 Fi、Fci和 Ffpi類似，M 為滾（gǔn）削力矩。以上是對單齒所受切削力的（de）計（jì）算，若要得到整個滾刀（dāo）切削過程的滾削力，則需將其轉換（huàn）至刀具，並在考慮時間因素（sù）的基礎上對各刀（dāo）齒上的滾削分力進行集成（chéng）。
   

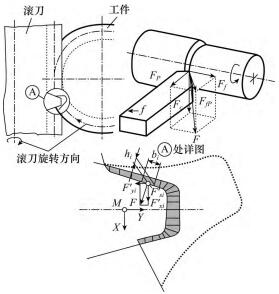
    圖 12 滾削單元分力確定
   
    圖 13 所示為測（cè）量結果與計算（suàn）結果，從滾削力變化周期和幅值（zhí）角度可以看（kàn）出實驗結果（guǒ）與計算結果較為一（yī）致（zhì），微（wēi）小誤差可能來自（zì）切屑流動［20］。除 KienzleVictor的計算（suàn）模型之外，Gutmann［20］、Bhattacharyya［34］、Toshio［16］、Kenichi［42］和 Ali［31，43］等人都對切削力做過較為詳盡的理論推導，綜合各種方法可以得出滾削力的理論計算常用思（sī）路如（rú）下。
 
    1) 確定切削區域。
    2) 計算切（qiē）屑等效厚度和等效寬度。
    3) 利用（yòng）公式 Fi = Ki × b × h計算滾削分力。
    4) 滾削分力（lì）集成。
 

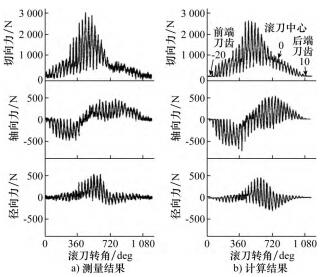
    圖13 實驗測量結果與計算結果比較
 
    在理（lǐ）論分析中，切削力係數可通過正交切削（xuē）實驗（yàn）得到，難（nán）點在（zài）於如（rú）何準確地確（què）定切削麵積、切（qiē）屑厚度和寬度。麵對上述難點，Bhattacharyya 等人采取間接方法，由（yóu）功-能（néng）關係計算出滾刀每轉切削特定體積時（shí）所做的（de）功（gōng）和消耗的能量［34］。除此之（zhī）外，Vedmar［32］等人通過大量計算（suàn）推導了未變形切屑的橫截麵積（jī）、最大切屑厚度、平均切屑厚度和切屑寬（kuān）度的微分方程，但推導過程極為複（fù）雜; Terashima［42］等人利用（yòng）幾何方法，對每個刀齒（chǐ）編號並將每（měi）個（gè）刀齒輪廓線劃分了節點，在（zài）對滾刀（dāo）和工件的接觸區域劃分切削層（céng）的基礎上推導了每個刀齒（chǐ）的切削區域以及切屑厚度和寬度; 初黎和Abood［38，43］在考慮運動關係和切屑層變化的基礎上，推導出了滾削（xuē）分力表達（dá）式，Abood［43］用 Matlab 編程語言實現（xiàn）了滾（gǔn）削力和力矩的模擬，模擬結果與試驗結果基本一致。
   
    大量計（jì）算結果表明: 滾削力變化與切屑寬度變化成正比，與切屑厚度關係較小［44］; 切屑參數與滾刀直徑密切相關，不同（tóng）形狀的切（qiē）屑（xiè）由不同的切削參數導致［45］; 刀具角度減小引起的滾削力上升可解釋為“切屑幹擾”現（xiàn）象（xiàng）［16］; 軸向進給增加導致（zhì）的切削力上升歸（guī）因於（yú）切屑厚度和寬度的增加; 每齒切（qiē）削力的波動由切屑厚度的變化（huà）引起。
   
    由此可以看出，目前對滾削力的研究，核心問（wèn）題是對切屑變形規律和未變形切屑幾何（hé）參數的確定，在（zài）有限元法還不能對滾削做（zuò）精確分析（xī）之時，如（rú）何更精（jīng）確地確（què）定滾（gǔn）削過程中切削區（qū）域及（jí）其麵積、未變形切屑的寬度、厚度和（hé）切屑的流動規律，是精確計算滾削力的前提。 
 
     4、 結果與討論
   
    與國外研究相比，國內滾齒切削力研究目前還局限於實驗測量階段，理論分析才剛起步［34，46-50］。實驗設備上，雖然都是基於傳統三向測力儀，但國外已應用無線遙測應變儀進行了一係列研究，且將紅外攝像（xiàng）機和高速攝像機［51］作為輔助設備，不僅能有效地觀察切（qiē）屑的產生和流動，而且能監測切削熱的產生及分布。理論分析上，國外基於金屬切削理論，對未變形切屑橫截麵參數著重討論，無（wú）論對切屑變形規律抑或滾削力都推導（dǎo）出了相應的公式，在一定條件下具有較高的準確度，而國內對於滾削力（lì）的理論研究少之又（yòu）少。軟件仿真（zhēn）上，國外已開發出模擬滾削加工的專用程序，能計算（suàn）每一（yī）層金屬切屑的變形程度（dù）和（hé）每個刀齒的切（qiē）削（xuē）分力以及滾刀每轉的切削分力，或利用 Matlab進行（háng）數值模擬，而國內（nèi）的相關報道較少，仿真往往局限於利用（yòng）通用（yòng）有限元軟件對單個刀齒進行受力分析，基於金屬切（qiē）削理論的仿（fǎng）真研（yán）究的報道也較少。
   
    因此，國內的滾削力（lì）研究需做大量工作，綜合起來應從三方麵（miàn）展（zhǎn）開: 1) 研製或搭建先進的測量平台;2) 從金屬切削原理入手（shǒu），分析切（qiē）屑產生（shēng）和變化（huà）的機理，推（tuī）導相應的滾削力公式; 3) 亟待開發專用的滾（gǔn）齒切削模擬軟件。從本文分析（xī）可看出（chū），滾削力的理論推導是開（kāi）發軟（ruǎn）件係統的理論基（jī）礎，因此，軟件開發歸根結底還是需要提（tí）高滾齒切削機理的理論研究水平。

     來源：常熟理工學院機械工程學院  江蘇省機電產品循環利用技（jì）術重點建設（shè）實驗室  蘭州理（lǐ）工大學機電工程學院