超精密(mì)車床主軸回(huí)轉誤差測試係統的研究
2016-12-14 來源:哈爾濱工業大學 作者:王世良
第 4 章
傾角運動誤差分離及實驗研究
本章將主要分析主軸傾角運動(dòng)誤差,在徑向運動誤差的基礎上推導傾角運動(dòng)誤差求解算法;進(jìn)行超(chāo)精密車床主軸傾角運動誤差(chà)實際測量實驗,並對不(bú)同轉速下主軸傾角誤差運動進(jìn)行研究。
4.1 傾角運動(dòng)誤差分析
4.1.1 軸線平均線的確定
為理解軸線(xiàn)平均線,我們先看一下國際(jì)機械生產(chǎn)研究學會(CIRP)對回轉軸(zhóu)線(xiàn)的定義。1976 年 CIRP 發表了“關於回轉軸性能的描述和測定”的統一文件,定義了回轉軸線(xiàn),即“回轉軸線是一條某指定物體(tǐ)繞(rào)其自身旋(xuán)轉的線段,此線段與該指定物體一起運(yùn)動,並相對於軸線平均線呈現出軸向、徑向和角向的運動。”文件對回轉軸的回轉(zhuǎn)軸線給出了以上明確定義,但是並沒有對回轉中心給(gěi)出明確定義[48]。
回轉軸線是(shì)回轉軸(zhóu)在任意一個瞬(shùn)時具備的屬性線,軸線平均線是(shì)一段(duàn)時間內對回轉軸線位置進行平均化得到的。在超精密(mì)車床主軸回轉誤差(chà)測量中,信號(hào)的同(tóng)步運動誤差,即是將主軸的回轉誤差運動作為周期性誤差運動(dòng)處(chù)理。在同步誤差運動中,軸線平均線即為主軸周期性回轉一(yī)周時,回轉軸線的平(píng)均位置。

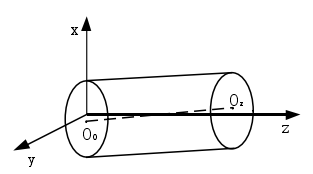
圖 4-1 回(huí)轉體軸線平均線模型

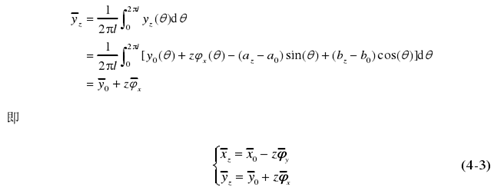
在上述方程處理過程中,我們假設回轉軸的回轉運動具(jù)有周期性。實際超精密車床主軸回轉誤差測量中,我們提取主軸的同(tóng)步運動(dòng)誤差,實際上就是將主軸的回轉誤差運動作為周期性運動(dòng)處理的。方程(4-3)為一空間直線方程,從方程(chéng)中(zhōng)看出,任意截(jié)麵中的任意點(diǎn)在回轉軸回轉一個周期(qī)內平均位置不變(biàn),這個平均位置點即為(wéi)平均回轉中(zhōng)心。雖然在推(tuī)導過程中,應用的是最小二乘圓心,但是沒有(yǒu)用到最小二乘圓心的任何性質(zhì),對截麵內任意一點,公式(shì)依然成立。上式中的空間方程即為軸線平均(jun1)線(xiàn),由平均回轉(zhuǎn)中心組成(chéng)。
從以上分析和概念可知:已知截(jié)麵內任意一點的運動軌跡,可求出此截(jié)麵的平(píng)均回轉中心;軸線平均線是一條空間直線,即各個截麵求出的平均回轉(zhuǎn)中心在一條空間直線上。所以說,已知任何兩截麵中任一點(diǎn)的(de)運動,都可以唯(wéi)一的求出回轉軸的軸線平均線。而軸線平均(jun1)線(xiàn)是求回轉軸(zhóu)傾角運動(dòng)誤差的絕對參考線,每個(gè)時刻回(huí)轉軸(zhóu)的瞬時回轉(zhuǎn)軸線(xiàn)與平(píng)均回轉軸線有一個相對位置。
4.1.2 雙截麵測(cè)量坐標係的(de)相對位置
回轉軸(zhóu)每(měi)個瞬時的回轉(zhuǎn)軸線(xiàn)與軸線平均線有一個(gè)傾角關係。回轉軸線是在雙截麵中的兩個測量坐標係中確定的,而平均回轉軸線在空間中是固定的,處於固連(lián)在大地上(shàng)的絕對坐標係中。所以在計算傾(qīng)角誤差之前(qián)首先要明確的是測(cè)量坐標係與絕對坐標係的位(wèi)置關係。
測量坐標係不(bú)能簡單(dān)地(dì)理解成由傳感器(qì)的布置(zhì)決定,也不(bú)要(yào)簡單(dān)地把三個(gè)傳感器軸線的交點當成測量坐標係的原(yuán)點。以下將對這兩個誤區進行分析。
傳感器布置如圖 4-2 所示(shì),兩傳(chuán)感器相互垂直對截麵進行(háng)測量。建絕對立坐(zuò)標(biāo)係 2,其原點是該(gāi)截麵最小二乘圓心回轉一周的平均(jun1)位置。坐標係 1為測量坐標(biāo)係。水平和垂直方向(xiàng)上(shàng)的傳(chuán)感器測量值記為S1(θ) 、S2(θ)。
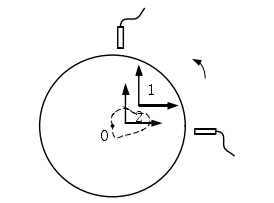
圖 4-2 測量坐標係與絕對坐標係的位置關(guān)係


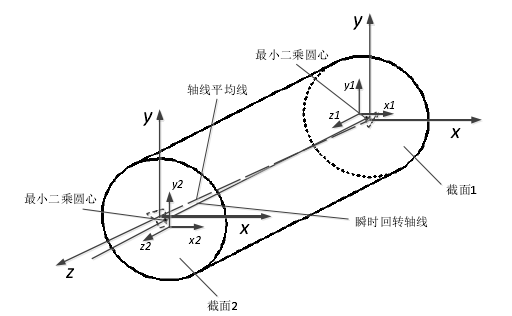
圖 4-3 雙截麵測量坐標係與絕對坐標係的位(wèi)置關係
4.1.3 傾角運動誤差計算
定義回轉軸的軸線(xiàn)平均線的意義在(zài)於給出決定傾角誤差運動的參考基準,以軸線平均線建(jiàn)立(lì)絕對坐標係,在此坐標係中計算回轉軸回轉周期內的傾角運動誤差。傾角運動誤(wù)差即是回轉軸每個瞬時的回轉軸線在絕對坐標係中對x 軸和 y 的轉角關係。
計算回轉(zhuǎn)軸的傾角運動誤差要對回轉軸(zhóu)的兩個截麵的回轉運動誤差進行測量,對兩個截(jié)麵的數據進行綜合處理得出傾角運動誤(wù)差。當(dāng)回轉軸以一定轉(zhuǎn)速穩定轉動(dòng)後(hòu),其軸線(xiàn)平均線在空間中是(shì)一條固定的直線,基於此線(xiàn)建(jiàn)立絕對坐標(biāo)係。每個截麵由傳(chuán)感器的安裝位置各自決定此截麵的測量坐標(biāo)係(xì),兩(liǎng)個(gè)測量坐標係(xì)在絕對坐標係中處(chù)於不同的位置。
兩個(gè)截麵數據要進行綜合處理的一(yī)個非常關(guān)鍵的因素是確定兩個截麵的測(cè)量(liàng)數據要轉(zhuǎn)化到一個坐標係中進行處理,否則結果(guǒ)就是失真的。測量數據是依賴於測量坐標係的,根據上節的結論,去掉直(zhí)流分量的傳感器測量值將依賴於絕對坐標係(測量坐標係與絕對坐標係重合),測量坐標係(xì)在(zài)絕對坐標係中的(de)位置,所以可以將測量坐標係的數據(jù)轉化到絕對坐標係中進行求解。
第(dì)一個測量截麵為定義為基準麵,在此(cǐ)截麵上測(cè)量的徑向運動誤差將作(zuò)為基準,通(tōng)過第二個截麵的徑向運動誤差(chà)來求得主(zhǔ)軸的傾角運動誤差(chà)。




主軸的兩個截麵上的(de)徑向運動誤差相差很小,對(duì)於一般主軸差(chà)值是微米(mǐ)級,對超精密車床來說此差值的數量級(jí)都是在亞微米級。而兩個測量截麵的(de)間距 l 是毫米級或是更大,所以公式(4-4)和公(4-5)可做如下簡化為
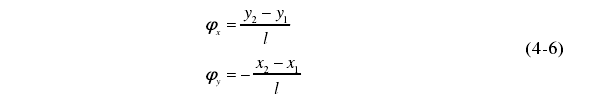
4.2 傾角運動誤差測量實驗及分析(xī)
4.2.1 傾角運動誤差測量實驗方案
傾(qīng)角誤差是指主軸軸線繞 x,y 軸的轉動傾角,測量時要對被測試件垂直(zhí)於軸線的兩個截麵進行同時測量。基於每個(gè)截麵需要 3 個位移傳感器進行徑向運動誤差的分離,如果進(jìn)行(háng)在線時時(shí)測量,則共需 6 個傳感器。鑒於實驗設備的(de)缺乏,傾角誤差試驗將分兩步進行。
第一步,對兩個截麵(miàn)分別進行三點法頻域誤差分離試驗,如圖 4-4。此(cǐ)步的目的是得到被測試件在(zài)各個(gè)截麵(miàn)的圓度誤差,同時也能得到(dào)主軸在此截麵平麵內的徑向運動誤差。
第二步,在兩(liǎng)個(gè)截麵內的 x,y 方向上同時架設 4 個位移傳感器,對主軸(zhóu)的誤差運動進行(háng)測量,如圖 4-5,數據處理將在下麵的小節中詳細介紹。

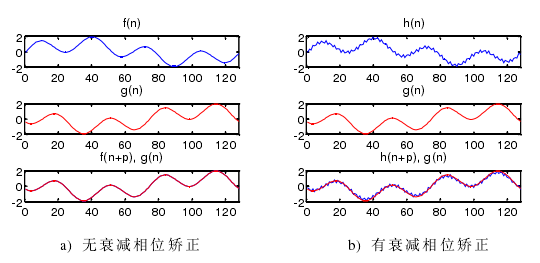
圖 4-6 相位矯正
4.2.2 相同(tóng)點位非同時測量值的相位矯正
因(yīn)為傾角運動誤差需(xū)要分兩次測量,而且本(běn)實驗所用超精(jīng)密(mì)車床的(de)編碼器是(shì)增量式(shì)而非絕對(duì)式的,給實際測量實驗帶來了一定困難。本節將研(yán)究傳感器在同一位置的兩次(cì)測量值(zhí)如何保證具有相同的測量起點。
給定一離散周(zhōu)期信(xìn)號 s(n),從信(xìn)號 s(n)中兩個不同點位開始分別取一(yī)個周期的數據,個數為 N。兩次(cì)采樣點序列記為 f(n),g(n),其中 g(n)=f(n+p),其中 p 為(wéi)兩信號的(de)相移點(diǎn)數。則問題歸化為已知(zhī) f(n),g(n),求兩個離散信號序(xù)列的相移點數 p。
對 f(n),g(n)做傅裏葉變換得


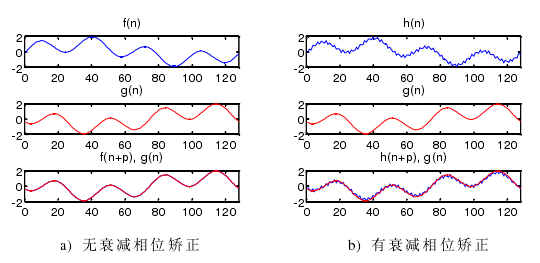
圖 4-6 相位矯正(zhèng)
4.2.3 傾角運動誤(wù)差分離實驗數據處理
傾(qīng)角誤差分離試驗(yàn)將按兩(liǎng)步進行,首先要到的(de)是被(bèi)測試件在兩個截麵內的圓度誤差。通過對每個截麵內三個傳感器采(cǎi)集的數(shù)據進行處理,得到被(bèi)測試件在此截麵內的圓度(dù)誤差信號。此時需要關注的是被測試件每個(gè)點位上實際值,後續雙截麵同時處理時要用到這(zhè)些具體值。
第一步操作(zuò)如下:
這裏不再贅(zhuì)述單截麵主軸(zhóu)徑向(xiàng)運動誤差和被測試件的圓度誤差,下麵直(zhí)接給出被測試件兩個截麵分別進行(háng)三點法誤差(chà)分離試驗的數(shù)據結果。表 5-1和圖 4-7 給出兩個截麵測量數據的最小二乘評價表和實際(jì)數據的(de)極坐標圖。
表 5-1 兩截(jié)麵分別測量得出的圓度誤差和徑向運動(dòng)誤差


圖 4-7 雙截麵分離出的圓度(dù)誤差(矯正(zhèng)前(qián))
雖然通過這一步已經分離出主軸在兩個(gè)截麵內主軸的徑向運動誤差,但是我們不能(néng)用這兩個截麵在這(zhè)一步測得的數據來求解主(zhǔ)軸傾角運動誤差。原因有二:第一(yī),這兩(liǎng)個截麵的三點法頻域誤差分離試驗是分開進行的,也就是(shì)說兩截麵的徑向運動誤差不是同時得到的;第二,本試驗所采用的超精密車(chē)床主軸電機編碼器(qì)不是絕對式編碼(mǎ)器,即便不考慮原因一,徑向運動(dòng)誤差圖也存在相位(wèi)移動。這些(xiē)問題(tí)將通過第二步來解(jiě)決。
第二(èr)步操作如下:
四個位移傳感(gǎn)器分別安裝在被測試件的(de)兩個截麵內 x,y 方向(xiàng)上(shàng),對主軸運動進行同時測量(liàng)。我(wǒ)們已知從每個傳感器采集數據中提(tí)取的同步運動誤差信號(hào)中隻包含被測試件的圓度誤差(chà)信號和主軸在此方向上的徑(jìng)向運(yùn)動誤(wù)差。而(ér)經過第(dì)一步試驗的處理我們(men)已知被測試件兩截麵的圓度誤差值(zhí),此時從任何一個傳感器的同(tóng)步運動誤差信號(hào)中減掉被測試件對應(yīng)點位(wèi)的圓度誤差值就會(huì)得到主(zhǔ)軸在此傳感器方向(xiàng)上的徑向運動誤差值。
四個傳感器同時測量可以解決第一步兩(liǎng)截麵徑向運動誤差非同時測量的問(wèn)題,鑒於試驗(yàn)用超精密車床主軸電機編(biān)碼器不(bú)是絕對編碼器,另一個需要解決的(de)問題是同一位置處的傳感器的兩次測量數據中相位匹配,此處的相位匹配是指測量點位的匹(pǐ)配對應,用(yòng)軟(ruǎn)件匹配的方法解決硬(yìng)件編碼器在(zài)此次測量試驗中帶來的(de)困難。
主軸電機轉速為 1000 r/min,傳感器采樣頻率設為 25600 Hz。主軸每旋轉一周(zhōu)采樣 1536 點,主軸轉動角度分辨率為 0.2344°,相當於每轉分度 1536線的編碼器。在同一位置處(傳感(gǎn)器的位置,而(ér)不是測試件的測點的位置)的傳感器兩次分別測量 20 轉數據,從兩次測量數據中提取的同步運動誤差(chà)信號分別記為(wéi)S1和S2 。因為沒有絕對編碼器,所以每次測量不能保證(zhèng)相同的起始測點。S1 和S2會在相位上出現偏差,如圖 4-8 a),利用算法矯正過的(de)圖形如圖 b)。
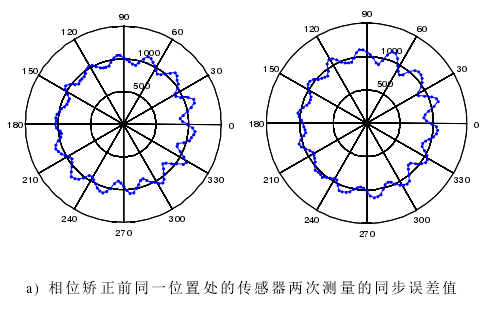
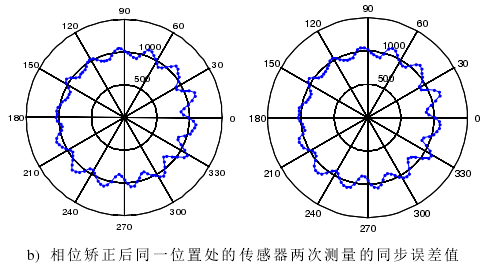
至(zhì)此,我們已經解決(jué)無絕對編碼器帶來的相位捕捉問題。主軸旋轉時對被測試(shì)件相同(tóng)位置處的兩次測量數據經過相位矯正後可以(yǐ)保證測量點位從同一點開始采集。從圖 4-8 b)可以看出(chū)相位矯(jiǎo)正(zhèng)效果是很好的。
將第(dì)一(yī)步和第二步傳感器信號進行相位矯(jiǎo)正後,從兩個截麵 x,y 方向上的傳感器的同步運動誤差(chà)中減掉第一步的(de)分離(lí)出的圓度誤差即(jí)可(kě)得到(dào)兩個截麵的徑向運動誤差,如圖 4-9 所示。
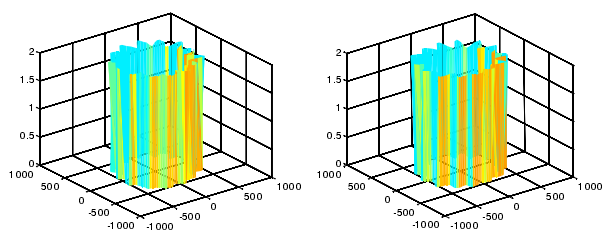
圖 4-9 左側圖為兩截麵 x 軸方向運(yùn)動(dòng)誤差,右側圖為兩截麵 y 軸方向運(yùn)動誤差
根據公式(4-8),可計算出主軸在(zài) x 軸和 y 軸方向上的傾角運動誤差,如圖 4-10 所示(shì)。
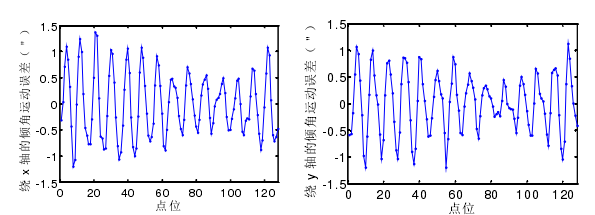
圖 4-10 繞(rào) x 軸和 y 軸的傾角運(yùn)動誤差
4.2.4 主軸(zhóu)轉速對傾角運動誤差的影響
上節分析的(de)是轉速在 1000 r/min 時,主軸繞 x 軸和 y 軸的傾(qīng)角運動誤差的分離過程。為研究主軸轉速對傾角(jiǎo)運動誤差的(de)影響,試(shì)驗還對主軸轉速在600 r/min 和 200 r/min 時進行傾角運動誤差的分離運動,試驗結果如圖 4-11。
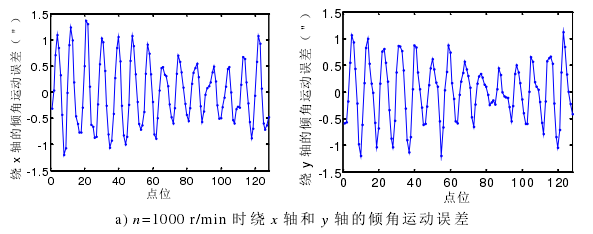
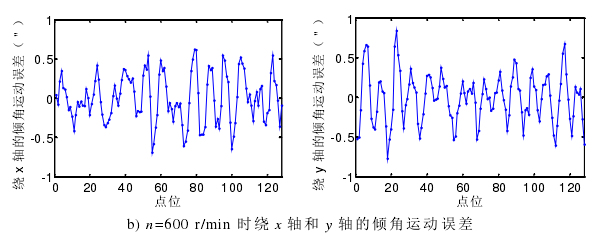
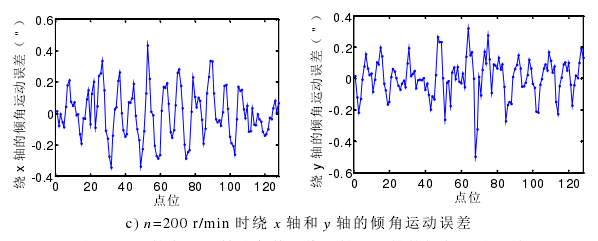
圖 4-11 主(zhǔ)軸(zhóu)在不同轉速條件下繞 x 軸和 y 軸的(de)傾角運動誤差
從圖 4-11 可(kě)知,隨著主(zhǔ)軸(zhóu)轉速的降低,傾角運動誤差隨之(zhī)減小。綜合(hé)之前分析的主軸的徑向回轉運動誤差(chà)隨主(zhǔ)軸轉速的降低而減小,可知(zhī)主軸的在 1000 r/min 以內轉動,轉速越低,其轉動穩定性越(yuè)好(hǎo)。
4.3 本章小結
本章主要分析雙截麵測量實驗數據在去掉(diào)直流分量後(hòu),是處在同一個坐標係——絕對坐標係中的,為傾角(jiǎo)運動誤差的計算提供有效數據;在徑向運動(dòng)誤差的(de)基礎上推導傾角運動誤差求(qiú)解算法;進行超精密車床(chuáng)主軸(zhóu)傾角運動誤差實際測量實驗,並對不同轉速下主軸傾角誤差運動進行研究。
結論
超精密(mì)主軸回轉(zhuǎn)誤差是(shì)影響加工工件表麵質量的最(zuì)主要因素,研究超(chāo)精密主軸回轉誤差對於評價主(zhǔ)軸回轉(zhuǎn)精(jīng)度,監測診斷主軸運行故障,預測機床加工工件表麵形狀誤差,加工誤差補償及提高機床加工精度等有重要意義。本文(wén)以三點法頻域誤差分離技術(shù)為基礎,以(yǐ)超精密車床主軸為研(yán)究對象,研究主軸的徑向運動誤差和傾角運動誤差的分(fèn)離。結論如下:
(1)從傳感器測量(liàng)值實際數學模型的解析構(gòu)成角度證明最小二乘偏心運動對主軸徑向誤差運動的不可分離性。給出實(shí)際測量環境下傳感器安裝角(jiǎo)位置偏差和安裝線偏差對誤差分離精度的定量分析,為超精密車床主軸回轉誤差納米級測量(liàng)采集數據的可(kě)靠性提高理論保證。
(2)在頻域中對除噪、濾波、同步運動誤差的提取以及三點法算法的前半部分進行連續性處理,減少測量信號(hào)在時域頻域中的變換計算。從超(chāo)精(jīng)密車床加工工(gōng)件表麵成形角度分(fèn)析去除一階諧波分量的依據。
(3)實際測出超(chāo)精密車床主軸徑向運動誤差,並根據推導出的主軸傾角運動誤差分離算法,測得超(chāo)精密車床(chuáng)主軸傾角誤差。
本文搭建的超精密車床主軸回轉誤差測試係統還存在一定的問題。雖然摒棄了安裝標準件到主軸上進行測量的方案,采用超精(jīng)密(mì)車床自身加工高精度測試件在無拆卸狀態下(xià)直接進行測(cè)量,依然不能很好地解決最(zuì)小二(èr)乘偏心運動對主(zhǔ)軸回轉誤差的影響。在今後的工作(zuò)中,將(jiāng)重點解決一下幾個問題:
(1)主軸徑向運動誤差的一階(jiē)諧波分量(liàng)與被測(cè)截麵最小二乘(chéng)偏心運(yùn)動量(liàng)的分離。一階諧(xié)波分量的分離同樣影響到傾角運動誤差(chà)的(de)分離,所以此問(wèn)題需待解決。
(2)主軸回轉誤差是影響超精密車(chē)床加(jiā)工對稱回轉(zhuǎn)體和快刀加工非對稱回轉體的表麵(miàn)質量最主要的因素,所以回轉誤差的加工補償(cháng)也是後續工作的重點。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進(jìn)行(háng)資訊合(hé)作,歡迎聯係本網編輯(jí)部(bù), 郵箱(xiāng):skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進(jìn)行(háng)資訊合(hé)作,歡迎聯係本網編輯(jí)部(bù), 郵箱(xiāng):skjcsc@vip.sina.com
更多本專題新聞
專題點擊前十
| 更多










