１　單對齒輪的齧合剛度模型（xíng）

      本文主要考慮在輸入轉速和負載扭矩不變的條件下，輸出齒輪轉角的變化情況。齧合剛度模型是一個最基本的齒輪副分析模型，隻考慮了齒輪副本身的影響因素，忽略了傳動軸的彎曲變形、扭（niǔ）轉變形和軸承的（de）支（zhī）撐剛度等。齒輪的（de）齧合剛度分析模型如圖１所示。

      其中，θｐ、θｇ分別（bié）為驅動（dòng）齒輪、從動齒輪（lún）的扭轉位移；

      Ｒｐ、Ｒｇ分別為（wéi）驅動齒輪、從動齒輪的（de）基（jī）圓半徑；Ｔｇ、Ｔｐ分別為負載轉矩和輸入轉矩（jǔ）；Ｊｐ、Ｊｇ分別（bié）為驅（qū）動齒輪、從（cóng）動齒輪的轉動（dòng）慣量；ｋｍ為輪齒的齧合綜合剛度；ｃｍ為輪（lún）齒的齧合阻（zǔ）尼。

      齒輪齧合剛度模型的建模條件是：驅動輪（lún）ｐ勻速轉（zhuǎn）動，負載（zǎi）扭（niǔ）矩Ｔｇ為恒定負載。假設在齧合線方向上齒輪的相對位移為ｘ，則ｘ＝Ｒｐθｐ－Ｒｇθｇ。由（yóu）於齒輪間的（de）齧合力Ｆｋｍ＝ｃｍｘ　·＋ｋｍｘ，則Ｆｋｍ為：

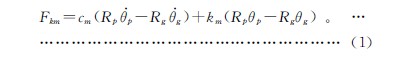
      齒輪副（fù）的動力學方程為：

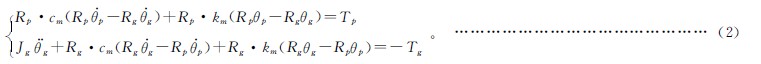
      ２　傳動鏈齧合剛度（dù）動力學模型（xíng）

      ２．１　直齒輪係統齧合剛度（dù）動力學模型［１］

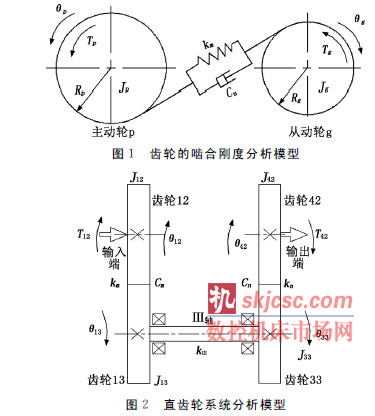
      在單對齒輪副（fù）齧合剛度分析模型的（de）基礎之上，考慮了傳動軸的扭轉（zhuǎn）剛度之後就形成了直齒輪（lún）子係統的動（dòng）力學模型，如（rú）圖２所示。其中，Ｊ１２、Ｊ１３、Ｊ３３、Ｊ４２分別為各直齒輪的轉動慣量；θ１２、θ１３、θ３３、θ４２分別為各直齒輪的旋轉角；Ｔ１２為輸入端的驅動扭矩；Ｔ４２為輸出端的負載扭矩；ｃｎ為（wéi）齒輪副的齧合阻尼；ｋｎ為齒輪副的齧合剛度；ｋⅢ為Ⅲ軸（zhóu）的扭轉（zhuǎn）剛度（dù）。

      直齒輪係統分析模（mó）型的前提條件是：輸入（rù）齒（chǐ）輪為勻速（sù）旋（xuán）轉運動，輸出負載扭矩為恒定負載。結合（hé）式（shì）（２）和牛頓力（lì）學理論，可以得到如下的微分（fèn）方程組：

      其中：Ｒ１２、Ｒ１３、Ｒ３３、Ｒ４２分別為（wéi）各直齒輪的基圓半徑。

      根（gēn）據Ｌａｐｌａｃｅ變換對式（３）進行處理，得到（dào）關於變量ｓ的多元一次方程組，代入（rù）設計數據（數據保密），得出直齒輪子係統動力學模型的轉角傳遞函數Ｇ４２為：

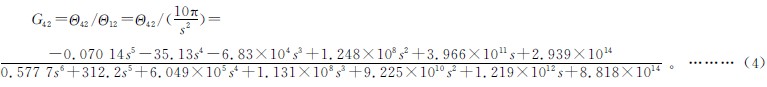
      其中：θ１２、θ４２分別是θ１２、θ４２的Ｌａｐｌａｃｅ變換。

      其（qí）中（zhōng）：ＲＳ、ＲＮ分別為太（tài）陽輪（lún）和行星輪的基圓半徑（jìng）。

      （２）內齒圈與行星輪在齧合線方（fāng）向上的相對位移δＲＮ為：

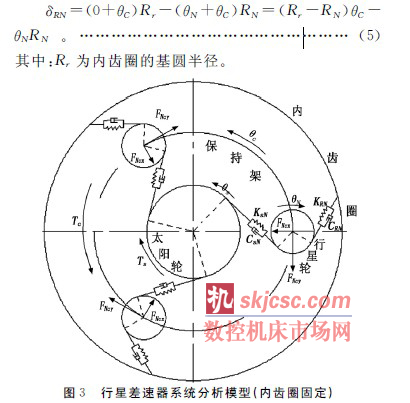
       ２．２．２　齒輪齧（niè）合力的計算

      （１）內齒（chǐ）圈與行星（xīng）輪的（de）齧合力ＦＲＮ為：

      將式（４）～式（８）代入到式（９）、式（１０）中，並轉（zhuǎn）化成方程組的形式為：

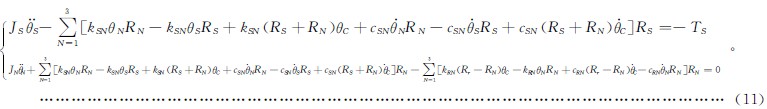
      式（１１）中的變量為：ＴＣ，θＳ，θ１，θ２，θ３。由（yóu）於θ１＝θ２＝θ３，故用θＮ來替代，使之滿足θＮ＝θ１＝θ２＝θ３。將
 

      式（１１）進行Ｌａｐｌａｃｅ變換，代（dài）入設計（jì）數據（數據保密）求得轉角（jiǎo）傳（chuán）遞函數ＧＣＳ：

      其（qí）中：θＣ、θＳ分別為（wéi）θＣ、θＳ的Ｌａｐｌａｃｅ變換形式。

     ３　傳動鏈動力學總模型

      將前麵（miàn）的直齒輪係統和行星（xīng）差速器係統的動力學模型進行綜（zōng）合，用轉角傳遞函數來表示（shì）最終的動力學模型。由於這兩（liǎng）個子係統（tǒng）是串（chuàn）聯關係，因此（cǐ）總傳動鏈（liàn）模型的轉角傳遞函數為（wéi）：

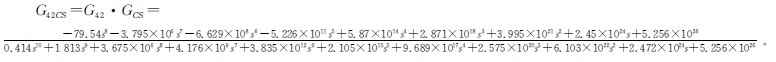
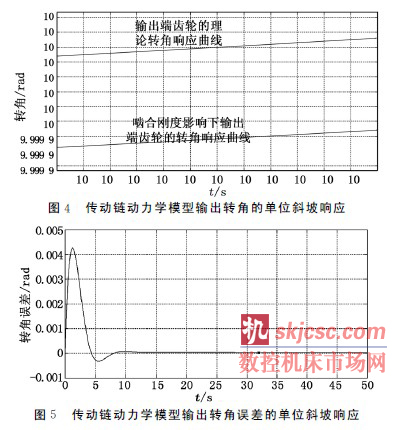
      運用ＭＡＴＬＡＢ軟件對轉（zhuǎn）角傳遞函數進行單位斜坡響應（yīng）分（fèn）析，得到的曲線如（rú）圖４、圖５所示。

      ４　結論

      由圖４、圖５可得出（chū）如下結論（lùn）：①在齧合剛度影響下的傳動鏈轉角的（de）輸出曲線與輸入曲線之間存在（zài）著轉角誤差，這會影（yǐng）響該（gāi）機床（chuáng）傳動鏈的傳動精度和傳遞的準確性；②轉角誤差響應曲線經過一定（dìng）的震蕩（dàng）後（hòu）期後，穩（wěn）定為一條（tiáo）水平的直線，這表（biǎo）明齧合（hé）剛度影響下的傳動鏈（liàn）轉角誤差（chà）是一個不隨時間變化的（de）恒定；③齒輪的（de）理論轉角（jiǎo）相應曲線的斜率與齧合剛（gāng）度模型下的轉角響應曲線斜率（lǜ）基本（běn）相同，說明齧合剛度對（duì）傳動鏈的傳動比基本沒有影（yǐng）響。