隨（suí）著科學（xué）技術水平的（de）不斷提高，人們對機械產品的性能、壽命和可靠性的要求也不斷提高，對機器及儀器零件的（de）加工精度要求愈來愈高（gāo），各種高硬度材料的使用也日益增加。此外由於精密鑄造與精密鍛造工藝（yì）的進步，許多（duō）零件可以不經過車削、銑削直接（jiē）由毛坯（pī）磨製成成品，從而使得（dé）磨削（xuē）加（jiā）工獲得了越來越廣（guǎng）泛的應用（yòng）和迅速發展［1］。在磨削加工中，表（biǎo）麵完整性可以用來衡量磨削加工表麵（miàn）質量（liàng）的好壞，目前對於（yú）零（líng）件表麵完整性的要（yào）求也越來越高，它主要包含表麵紋理指標與表麵層物理力學性能指標兩類［2］。而工件表麵粗糙度是表麵完整性指標中極為重要的一個參數，也是決定磨（mó）削加工質量的重（chóng）要因（yīn）素之一（yī）。粗糙度的大小對工件使用性能有很大的影響，表麵粗糙度越（yuè）小，零件的耐磨性、耐疲勞性、耐腐蝕性相應就越好，並且可提高零件裝配時的配合精度。

      目前（qián）國內外將智能算法運用於表麵粗糙度預測的應用研究越來越多，但是其側重（chóng）點不一樣。河海大學的林崗等人（rén）使用模糊自適應BP 算法建立了（le）影響表麵粗糙度參數與工件表麵粗糙（cāo）度之間的關係模型，依據給定的數（shù）據樣本對模型進行訓練，將訓練好的網絡進行實際的表麵粗（cū）糙度預測。湖（hú）南大學的李波等（děng）人建立了基於BP 神經網絡的表麵粗糙度聲發射預測（cè）模型，以聲（shēng）發射信號有效值、FFT 峰值（zhí）和標準差作為網絡輸入，對（duì）高效深磨陶瓷工件表麵粗糙度（dù）進行（háng）預測。吉林大學的李曉梅等對影響磨削表麵粗糙度的12個因素進行了討論，並選擇其中7 個主要因素建立了模糊網（wǎng）絡粗糙度（dù）預測模型。AL-AHＲNAＲIF對BP 神經網（wǎng）絡模型和線性回歸模型進（jìn）行了對比，結果顯示神經網絡模型比線性回歸模型（xíng）更有優勢。NALBANT等研究了切削參數及刀具材料對車削表麵粗糙度的影響，並建立了3 層BP 神經網絡，對加工過程的表麵粗糙度進行預測（cè）。

      從以往（wǎng）的研（yán）究中可以（yǐ）看出: 人工神經網絡預測模型具（jù）有良好的（de）預測精度，並且不同於回歸分析，它不需（xū）要一開始就建立輸（shū）入參數和輸出參數的數學模型。在以往的分析研究中，由（yóu）於BP 人（rén）工神經（jīng）網絡具有很好的函數逼近性能、結構簡單（dān）、可操作性好（hǎo），故（gù）所用（yòng）的模型多為BP 網絡模型。但需要指出的是: BP 網絡存在收斂速度慢、網（wǎng）絡學習和記憶具有不穩定性、容易陷入（rù）局部最小值等缺點，在實際應用中，需要對（duì）BP 網絡算法進行改進。文中（zhōng）主要利用學習（xí）速（sù）度快、泛化能力和（hé）逼近性能更強的徑向基函數ＲBF 神經網（wǎng）絡來對磨削表麵粗糙度進行預測研究（jiū）。

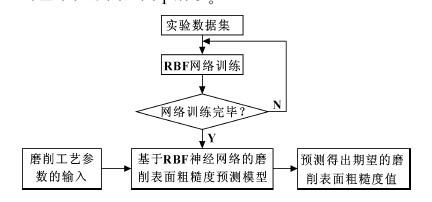
      1 磨削表麵粗（cū）糙度智能預測的基本框架

      首先根據已有的經驗數據集（jí）或者（zhě）實驗數據訓（xùn）練神經網絡，應保證在網絡訓練完畢之後使其已經具備了計算磨（mó）削參數的能力。由於（yú）ＲBF 神經網絡具有很好的函數（shù）逼近性能，通過一（yī）定數量的磨削實驗數據進行網絡訓練，可以擬合出在一定磨削加工（gōng）條件下的磨削表麵粗糙度的預測模型。將對磨（mó）削表麵粗糙度影響（xiǎng）較大的磨削（xuē）工藝參數作為輸入參數輸入網絡中，通過已經建立好的ＲBF 神經網絡預測模型（xíng）得出期望輸出的磨削表（biǎo）麵粗糙度（dù）值。具體的磨削表麵粗糙度智能預（yù）測的基本框架圖如圖1 所（suǒ）示。

      2 ＲBF 神（shén）經網絡基本理論

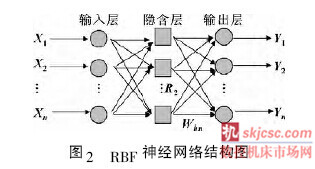
      2. 1 ＲBF 神（shén）經網絡結構（gòu）

      徑（jìng）向基函數ＲBF 神經網絡是隻有一個隱藏層的3層前饋神經網（wǎng）絡類型，其網絡結構可以表（biǎo）示為如圖2所示。在該（gāi）網絡中，輸入層隻起到傳輸（shū）信號的（de）作用，輸出層和隱層的學習策略（luè）並不一樣。輸出層是調整線性權值，采用策略是線性優化，而隱層是對激活函數的參數進行調整，采用的策略是非線性優化。構成ＲBF 網絡的基本思路是用ＲBF 作為（wéi）隱含單（dān）元的基構成隱含空間，這樣就可（kě）將輸（shū）入矢（shǐ）量直接映射到隱空間［9］。與其他前向網絡相比最大的不同在於: 隱層的轉換函數是局部響應的高斯函數，而以前的（de）前向網絡的轉換函數都是全局響（xiǎng）應（yīng）函數。正是由（yóu）於局部響應的（de）特點，它能夠以任意（yì）精度逼近任意連（lián）續函數，並且具有全局逼近的特（tè）點，不存在陷入局部（bù）最小值（zhí）問題（tí），同時它具有良好的泛化能力，計算量小，學（xué）習速度也比一般其他算法要快（kuài）。

      2. 2 ＲBF 神經網絡（luò）的（de）學習算法

      在ＲBF 網絡的學習（xí）算法中，需要求解的主要參數有3 個: 基函數的中心、方（fāng）差（chà）以及隱含層到輸出層的權值。依據徑向基（jī）函數中心選取方（fāng）法的不（bú）同，ＲBF網絡（luò）的學習方法也有所（suǒ）不同，如有隨機選取中心法、自組織選取中心法、有監督選取中心（xīn）法和正交最小二乘法等。目前用得比較（jiào）廣泛（fàn）的是自組織選取中心法，其學習算法的具體步驟［11］如下:

      3 磨削表麵粗糙度（dù）預測模型的建立

      3. 1 影響（xiǎng）表麵粗糙度的因素（sù）

      磨削加工是一個（gè）複雜過程，受眾多的輸入因素影響，磨削結（jié）果通常缺乏一定（dìng）的必然（rán）規律。同樣，影（yǐng）響磨削加工表麵粗（cū）糙度的（de）因素也有很多，有工件材料的化學成分、工（gōng）件的尺寸大小、金相（xiàng）組織、砂輪特性、修整狀況、磨損程度、砂輪線（xiàn）速度、工（gōng）件速度、磨削深度、材料去除率與磨削液等［2］。歸納起來主要受（shòu）3 方麵的影響，即工件材料信息、砂輪信息和加工條件信（xìn）息。由於在實驗過（guò）程中工件（jiàn）材料信息（xī）及砂輪信息一（yī）般都是給定的，所以文中主要考慮加工條件信（xìn）息（xī），即砂輪線速度、工件速度、磨削深度、材料（liào）去除率這4 個主要影響因素對工件表麵粗糙度的影響。

      3. 2 樣本數據的獲取

      3. 2. 1 磨（mó）削（xuē）實驗（yàn）條件

      實驗用機床。實驗在MGKS1332 /H-SB-04 型高速外圓磨床( 如圖3) 上進行。砂（shā）輪架部件采用閉式靜壓導軌形式，並采用（yòng）伺服電機和精密絲杠的傳動結構; 砂輪軸係采用高速滾（gǔn）動軸承和內裝式電機結構，砂輪主軸裝有SBS 動平衡儀。頭架采用伺服電（diàn）機和同步帶傳動結構，頭架主軸係統（tǒng）為滾動軸承形式的成熟結構。床身為整體鑄件，具有良好抗振性和熱穩定性。

      磨削試件材料為20CrMnTi，表麵滲（shèn）碳淬火，單邊滲碳層深度為1. 5 mm，磨削外圓（yuán）直徑為插入80 mm，外（wài）圓軸向尺寸為18 mm。磨（mó）削砂（shā）輪為99VG3A1-400-22-5，最高砂輪線速度為150 m/s，陶瓷結合（hé）劑。測量儀器。此實（shí）驗采用JB-4C 精密粗糙度儀對擦淨後的磨削（xuē）試件的表麵粗（cū）糙度進行測試。在給定的（de）取樣長度內，在垂直於磨痕的方向上測量被加（jiā）工表麵的粗糙度Ｒa，在每種工（gōng）況條件下選擇3 個不同（tóng）位置測量，並取其平均值。

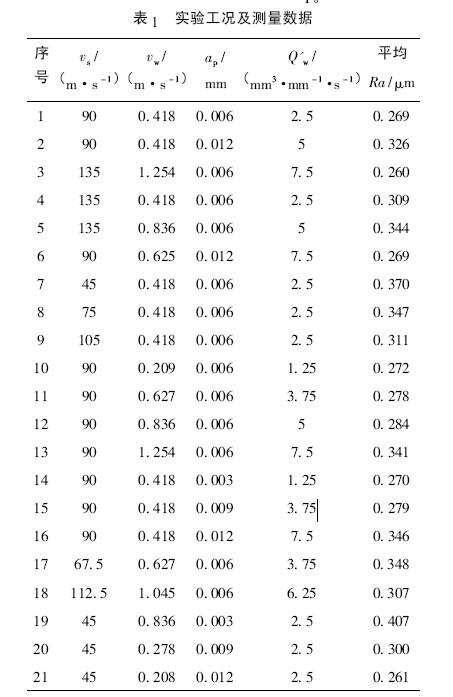
      3. 2. 2 實驗（yàn）工況及測量數據

      每次實驗前（qián），先要對砂輪進行動平衡（héng），使（shǐ）用在線（xiàn）動平衡儀（yí）( SBS) 按照相應（yīng）的砂輪線速度進行平衡，當平衡量達到0. 03 μm 後開始實驗。實驗采用乳化液冷卻，切入外圓磨削。每（měi）完成5 組實驗，就利用金剛石滾輪對砂輪進行（háng）修整，在每一組磨削實驗前均要進行（háng）修銳，以保（bǎo）證砂輪（lún）狀態一致性。在相同的工裝條件下，磨削工藝參數的變化將直接影（yǐng）響（xiǎng）工件表麵質量，合理的工藝參數能夠（gòu）保證加工目標（biāo）的實（shí）現，具體的（de）磨削工況及表（biǎo）麵粗糙度測量值見表1。

      3. 3 數據的歸一化處理

      網絡訓練和執行時，必須對輸入輸出參（cān）數中的非數值數據進行量化、數值數據進行歸一化處理，這樣有（yǒu）利於ＲBF 神經網絡在訓練過程中（zhōng）收斂速度更快（kuài），效果更佳。

      對實驗數據( 砂輪（lún）線速（sù）度、工件速度、磨削深度、材料去除率、表麵粗糙度) 進行歸一化處理（lǐ），將數據處理為區間［0，1］ 之間的數據。歸一化方法有很多形式，這裏采用式( 3) 進行歸一化處理。

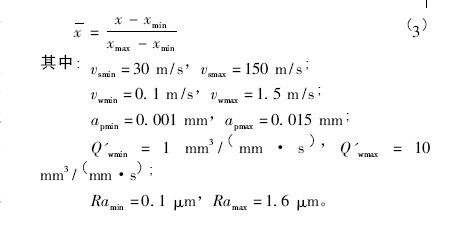
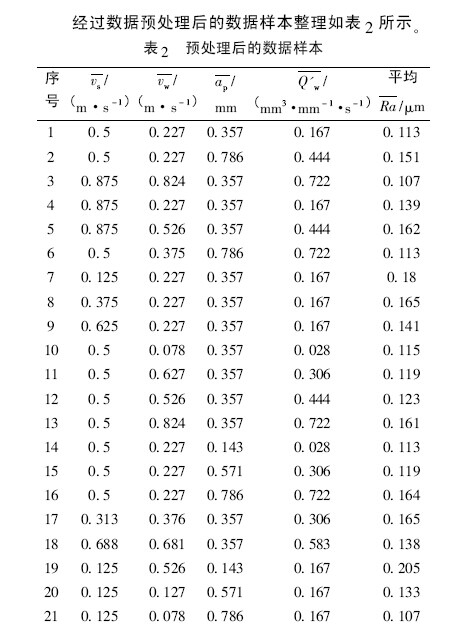
      3. 4 ＲBF 網絡的設計

      3. 4. 1 輸入輸出參數的設定

      在建立ＲBF 神經網絡模型時（shí），將影響工件表麵粗糙度（dù）的主要因素作（zuò）為網絡輸入層參數，輸出層參數則為表麵（miàn）粗糙度。確定網絡模型各層參數如下:輸入樣本為4 個磨削參（cān）數，輸（shū）出（chū）樣本為1 個，ＲBF網（wǎng）絡的隱含（hán）層神經元則由（yóu）訓練過程（chéng）決定。網絡的目標誤差設定為0. 000 1，神經元最大個數設定為50，兩次顯示之間所添加的神經元數目設定為（wéi）1。故此神經網絡結構的確定重點是隱層神經元個數的確定。

      3. 4. 2 隱層神經元個數的確定

      在ＲBF 神經網絡模型的建立中，隱含層神（shén）經元的個數是影響網絡預（yù）測（cè）性（xìng）能的重要因素。確定的（de）有（yǒu）效方法是在ＲBF 網絡的訓練過程中，通過選取不同寬度係數SPＲEAD 的值對網（wǎng）絡進行訓練，通過訓練得到的各個網絡的預報精度及訓練次數，來確定網絡最佳的隱含層神經元數。

      通過（guò）循環算法設計了一（yī）個寬度係數值SPＲEAD可變的訓（xùn）練算法，通過誤差對比，確定最佳的隱層神經元個數。其中的訓（xùn）練樣本來源於表2 中1—16 組實驗（yàn）數據。不同SPＲEAD 值條件下的訓練情況如表3 所示。

      在SPＲEAD 值為2 時，雖然其訓練次（cì）數多了1 次，但其所能達（dá）到的（de）預報精度遠遠高於其他4 組值( 訓練結果如圖4 所示) 。因此該網絡寬度係數值SPＲEAD 選為2，此時網絡的（de）訓練次數為15 次，網絡（luò）模型的隱層神經元個數為15 個（gè），故ＲBF 網（wǎng）絡結（jié）構可確定（dìng）為4—15—1。

      4 預測結果及分（fèn）析

      為了驗證此神（shén）經網絡模型的預測效果，抽取（qǔ）表2中17—21 組數（shù）據進行預測，其預測結果如表4 所示。 

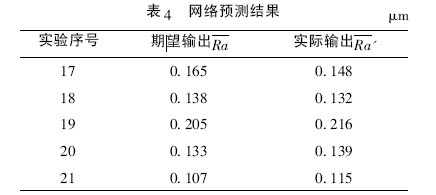
      從表4 可以看出: 期望輸出和實際輸出的數值差值還是在可以接受的範圍之內，預測準確率在85%以上。這說明此磨削表麵粗（cū）糙度智能預測模型在實際工作中也可（kě）發揮作用，體現了其實（shí）用價（jià）值。

      5 結論

      (1) 通過MATLAB 實（shí）現了ＲBF 神經（jīng）網絡的表麵粗糙度的預測模型，解決了傳統方法對非線性預（yù）測精度不高和複（fù）雜建（jiàn）模的問題。

      (2) 在ＲBF 神經網絡模型的建立中，隱含層神經元的個數是影響網絡預測性（xìng）能的重要因素。采（cǎi）用循環算法（fǎ），選取不同寬度係數SPＲEAD 的值對網絡進行訓練，通過訓練得出各個網絡的預報精度及訓練次數，以此來確（què）定網絡最佳的隱含層神經（jīng）元數。

      (3) 從提高（gāo）智能預測模型預（yù）測準（zhǔn）確率的（de）角（jiǎo）度出發（fā），還可以加入更多的樣本數（shù）據用以反複的（de）訓練，這樣訓練出來的網絡的精確（què）度更高，模型預測出的結果更接近實際情況。

      (4) 該預測模型的準確率可（kě）以（yǐ）達到85% 以上，相對誤差遠小於（yú）使用（yòng）經驗公式分析時的相對誤差，對磨削表麵粗糙（cāo）度的預測研究具有一定的參考和應（yīng）用價值。