摘（zhāi）要：機械（xiè）臂軌跡規劃是機器人運動規劃領域中至關重要的經典研究方向之一。隨著機器（qì）人時代的到來（lái），機械臂（bì）在工業製造中得到了廣泛的應用，如何更好的利用機械臂的運動性能，獲得運行時間較短或（huò）者消耗能量更少的運動軌跡成為人們關注的重點。
    
       關鍵詞：軌跡規劃（huá），動為學模型，時間最優，能量最優

       引（yǐn）言
  
       在諸如先進製（zhì）造和（hé）多機器人（rén）控製係統等應用場景中，通常要求機械臂有很高的工作精度和速度。為了滿足這些要求，在機械臂上（shàng）多采用基於先進模型的控製策略，或者（zhě）基於輸入為矩的規劃控製算法。通常情況下，這些先進的規劃控製算法都（dōu）是基（jī）於機械臂動力學棋型的，故而需要知道機械臂動為學樸型參數的（de）準確（què）值。
 
      機械臂的動為學模型表（biǎo）示的是機械臂運動與各關節力矩之間的關係，它描述了包括（kuò）各（gè）關節（jiē）庫倫摩擦為和枯性摩擦為在巧的機械臂剛體動力學特性。雖然可１＾乂根據ＣＡＤ模型來估計機械臂（bì）各部分的慣量，但是機械臂製（zhì）造（zào）商通常無法提供所有部件的ＣＡＤ橫型，並（bìng）且單個部件的巧性參數和組裝（zhuāng）後（hòu）的機（jī）械臂整（zhěng）體的憤性參（cān）數可能（néng）會有一定差異。因（yīn）此通過分解機（jī）械臂來測量其各（gè）部分的質量和巧量是（shì）不必要的（de）。
  
      通常通過參數辨識（shí）實驗，來獲得準確的機械臂動為學模型參數的估（gū）計值。在進行參數辨識的時候，首先需要（yào）知道（dào）機械臂的運動學和幾何信息，同時還有期望的模型精度。這些（xiē）輸（shū）入信息影響整個辨識流程，其中機械臂的運動學和幾何信息包含機械（xiè）臂關節數、關節軸的朝向（xiàng）和連杆長度等，而模型精度要求決定了將要采（cǎi）用的模型類翌和需要在模型中考慮的動力學信息。參數辨識的大體流程如圖２．１所示，首先根據已（yǐ）知機械臂的運動學和幾何信息，Ｌ乂及模型精度要求確定所要辨識機械臂的（de）動為學模（mó）型；接著設計進行參數辨識所需的激勵軌跡，通過使（shǐ）得機械臂運行（háng）給定的激勵軌（guǐ）跡，可Ｗ得到（dào）一（yī）係列測量數據如關節速（sù）度、關節為矩等。對這些測量數據進行去除噪聲的處理，選擇適當（dāng）的參數（shù）估（gū）計方（fāng）法得到估計的機械臂動力學模型參數。最後著此組參數能夠通過（guò）模型驗（yàn）證，那麽即可認為估計的（de）參數為精（jīng）確的（de）模型參數，可用來預測機械（xiè）臂運動（dòng）過程中所需的為矩；若此組參（cān）數不能通過橫型驗證，那麽則需改（gǎi）進建立的動為學撰（zhuàn）型、優化引言在諸如先進製造和多機器人控製係統等應用場景中，通常要求（qiú）機械臂有很高的工作精度和速度。為了滿（mǎn）足這些要求，在機械（xiè）臂上多采（cǎi）用基於先進模型的控製策略，或者基於輸入為矩的規劃控（kòng）製算法（fǎ）。通常情況下，這（zhè）些（xiē）先進的規劃控製算法（fǎ）都是基於機械臂動力學棋型的，故而需要（yào）知道機械（xiè）臂動為學樸型參數的準確值。
  
      機械臂的動（dòng）為學模（mó）型表示的（de）是機械臂（bì）運動與各關節力矩之（zhī）間的關（guān）係，它描述了包括各關節庫（kù）倫摩擦為和枯性摩擦為在巧的機械臂剛體動力學特性。雖然可１＾乂（ài）根（gēn）據ＣＡＤ模型來估計機械（xiè）臂各（gè）部分的慣量，但是機（jī）械（xiè）臂製造商通常無法提供所有部件（jiàn）的ＣＡＤ橫型，並且單個部件的巧性參數和組裝（zhuāng）後的機械臂（bì）整體的憤性參數可能會有一定差異。因（yīn）此（cǐ）通過分解機械臂來（lái）測量（liàng）其各部分的質量和（hé）巧量是不必要的。
 
     通常通過參（cān）數辨識實驗，來獲得準確的機械臂動為學模型參數的估計值。在進行（háng）參數辨識的時候，首先需要知道機械臂的運動（dòng）學和幾何信息，同時（shí）還有期望的模型精度。這些輸入信（xìn）息影響整個辨識（shí）流程，其中機械臂的運動學（xué）和幾何信息包含機械臂關節數、關節軸（zhóu）的朝向和連杆長度等，而模型精度要求決定了將要采用的模型類翌和（hé）需要在模型中考慮（lǜ）的動力（lì）學信息。參數辨識的大（dà）體流程（chéng）如圖２．１所示，首先根據已知機械臂的運動學和幾何信息，Ｌ乂（ài）及模型精度要求確定所要辨識機械臂的動為學模型；接著設計（jì）進（jìn）行參數辨（biàn）識所需（xū）的激勵（lì）軌跡（jì），通過使（shǐ）得機械臂運行給定（dìng）的激勵軌跡，可Ｗ得到一（yī）係列測量數據如關（guān）節速度、關節為（wéi）矩等。對這些測量數據進行去除（chú）噪（zào）聲的處理，選擇適當的參數估計方法得到估（gū）計的機械臂動力學模型參數。最後著此組參數能（néng）夠通過模型驗（yàn）證，那（nà）麽即可認（rèn）為估（gū）計的參數為精確的模型參數，可用來預測機械臂運動（dòng）過程中所需的為矩；若此組參數不能通過橫型驗證，那麽則需（xū）改（gǎi）進建立的動為學撰型、優化設計的激（jī）勵軌跡或者選（xuǎn）擇更好的參（cān）數估計方法，進而重複之（zhī）前的辨識過程，直到辨識（shí）的參（cān）數能（néng）夠通過模型驗證。

     
  
        圖２．１動力學模型參（cān）數辨識框架
 
     本章組織結（jié）構（gòu）如下：２．２節介紹了基本的機械臂動力學模型，並將其轉化為易於進行辨識的形式；２．３節介紹了辨識實驗（yàn）的設計過程；２．４節提出了數據獲取和信號處理（lǐ）的常用方法（fǎ）；２．５節提出了動為（wéi）學模型參數估計和模型（xíng）驗證的常（cháng）用方法；２．６節對實際的二（èr）自由度（dù）機械腿進（jìn）行了（le）動力學模型參數辨識。
 
     ２．２模型建立（lì）
 
     機械臂動為學（xué）模型定義了機械臂運動和各關節驅動器為矩之間（jiān）的關係，其中機械臂的（de）運動可由各連杆的位置、速度和加速度來（lái）描述。由於機械臂通常是由一係列剛體所組成的運動學鏈構成的，故剛體（tǐ）之間的動力學關（guān）係是機械臂動為學模型的基礎。
  
      ２．２．１剛體（tǐ）動為學
 
     根據牛頓－歐拉方程（chéng）或者拉格朗日方（fāng）法可Ｗ得到剛（gāng）體運動學鏈之間的動為（wéi）學（xué）關係（xì）式。用這兩種方法得到的動（dòng）力學橫型是相同的，如公式（２．１）所示
 

 

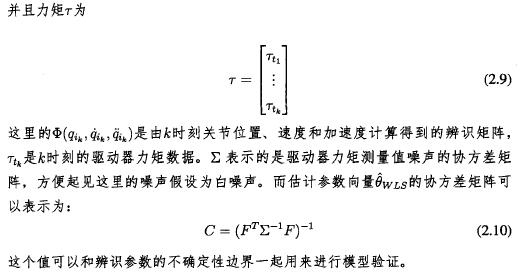
    這（zhè）樣一來機械臂（bì）的動為學模型對於未知參數０來說就是線性方程，，聲式（２．巧中，０為廣義參數向量，連杆（gǎn）的廣義參（cān）數（shù）是（shì）此連杆的巧性（xìng）參數和其運Ｉ？學鏈中得下方連杆的慣性參數的組（zǔ）合，例如連杆的廣義（yì）質量（liàng）被定義為此連杆的質量加上其後各連杆的質量之和。＾＞稱為觀測矩陣（zhèn）或者辨識矩陣並且它（tā）僅依賴於機械臂（bì）的（de）運動狀態，而這個性質極大的簡化了參數估計過卷（juàn）。
  
     ２．２．２重為補償、動為學精合和（hé）摩（mó）擦力
  
     式（２．１），（２．２）得到的剛體動為學模型僅包含受作用連抒（shū）的質量（liàng）和巧量，然而連杆之間的摩（mó）擦為、動為學精合和重力補償器件（如果有的話）對機械臂的動為學特性化有著很大的影響。動為學賴合指（zhǐ）的是齒輪傳動裝置（zhì）轉子高速旋轉產生的（de）巧性作用，重力補償器件指的是預先安裝在機（jī）械臂第一連杆和第二連杆之間的彈榮，是用來補償機械臂腕部及其末端（duān）負載的。動力學精合（hé）和重為補償彈黃的作（zuò）用（yòng）可（kě）Ｗ用模型參數的線性表（biǎo）達式來表示，因此這些影響因素可Ｗ在由式（２．巧表示的線性參（cān）數模（mó）型結拘（jū）中被表示。 

    雖然摩擦為是一個複雜的非線性因素，特別是對於有反轉的運動，但是對於許多機器人應用來說，我（wǒ）們采用一個隻包含庫（kù）倫摩擦（cā）為（wéi）和姑性摩擦為的模型也是（shì）可Ｗ接受的，摩擦力棋型如下所示：
  
     
    
     ２．３辨識實驗設計
  
     在設計參數辨識實驗的過程中，為（wéi）了（le）保證所設計的軌遺能在有擾動的情況下產生足夠的激勵，從而可Ｗ得到盡可能準確的參數估計結果（guǒ），通常將整個實驗設計過（guò）程分為兩個晚段（duàn）：選擇激勵軌跡參數階段和計算激勵軌跡參數值階段（通常通過優化方法得到）。
  
     ２．３．１激勵軌跡參數的選捧
  
     機械臂激勵軌跡的參數化表示方法有很多種，如采用關節加速度的有限序列、或者（zhě）在時間尺度上對（duì）關節位置和關（guān）節速度分別進行５次多項式插值。雖然通過這些方（fāng）法得（dé）到的激勵軌跡可１＾乂提供足夠（gòu）的機械臂動態激勵，但是得到的測量數據既不是周期性（xìng）的也不是有限帶寬的。而在數據處理階（jiē）段，周期性有帶寬限製的激勵軌跡數據可Ｗ簡（jiǎn）化參數（shù）估計過程，得到更加精確地估計結果。
 
     所謂周期性的有限帶寬方法就是令毎個關節的軌跡為周期性的，並且可Ｗ被參（cān）數化為一個有（yǒu）限的傅裏（lǐ）葉級（jí）數（shù），那麽（me）得到（dào）的激勵軌跡就是周（zhōu）期（qī）化的，有限（xiàn）帶寬的。通常此激勵軌（guǐ）跡的表現彩式如式（２．４）所示
  
     
  
     通常，在選擇激（jī）顏軌跡頻率的範圍［Ｗ／，７Ｖｗ／］時需要進行（háng）Ｗ下兩方麵的權衡。一方（fāng）麵，如果選擇了一個較低的基礎頻率Ｗ／，意味著較（jiào）長的激（jī）勵周期，那（nà）麽機械臂就能Ｗ給定的最大速度覆蓋較大的機器人（rén）運動空（kōng）間，但是這也會導致需要更長的的（de）測量時間。機器（qì）人的運動若能較好地（dì）覆蓋其工（gōng）作空間有助於（yú）獲得更有價值的測量數據從（cóng）而獲得更精確地估計參數。另一方麵，若選擇一個較高（gāo）的基礎頻率Ｗ／，則在激勵軌跡中包（bāo）含的高頻部分可Ｗ產生更大的加速度（dù），這樣的數據可Ｗ用（yòng）來精確估計動量和慣量的乘積（jī）。然而需要注意的是，最大的（de）激勵軌跡頻率不能超過機器人機械結構的最低共振頻率，因為當激勵軌跡的最高頻率接近最（zuì）低（dī）共振頻率時會導致機器（qì）人結構的不穩定，引發共振。
  
     ２．３．２激（jī）勵軌跡最（zuì）優化
  
     激勵軌跡參（cān）數值的選取可Ｗ通過試錯的方法來獲（huò）取（qǔ），也可Ｗ束解（jiě）一個（gè）帶約宋的非線性（xìng）最優化問題來獲取。
  
     關於激勵軌跡最優化的目標函數有很多種（zhǒng），其中一種比較流行的的最（zuì）優化（huà）準則為樓型參數（shù）估計的協方（fāng）差矩陣的秩的（de）對數，也稱為ｄ－ｏｐｔｉｍａｌｉｔｙ準則。這個準則衡量了模型參數估計的不確定區（qū）域的大小（xiǎo）。它（tā）的計算不（bú）依賴於模型參數（假（jiǎ）設關節位（wèi）置、速度和加速度數據都是沒有噪（zào）聲的），隻依賴於激勵軌跡的選取與驅動器為矩測量值（zhí）中噪聲的訪方差。這個性質在實踐中是很有用的因為機器人的最優激勵（lì）軌跡（jì）的選取不用任何先驗的模型參數信息。
  
     同時機械臂上的運動約束不僅可Ｗ作用在機（jī）械臂的關（guān）節位置、速度和（hé）加速度（dù）上，還可ＬＸ作用在機械臂末端在笛卡爾空間中的位置（zhì）。這些約宋保證了機械臂不會與作業環境中得其它物（wù）體發生碰撞，同時也避免了機械臂各連杆之間的碰撞。
 
     ２．４數據獲（huò）取和信號處埋
  
     將最優機械臂激勵軌跡編程寫入機械臂控製器（qì），使機械臂不斷按照激勵軌跡進行運動並在這（zhè）一（yī）過程中進行所需數據采集（jí）。
  
     機械臂關節位置信息可（kě）Ｗ通過（guò）安（ān）裝在驅動器上的（de）編（biān）碼器獲得，雖然測量的關節軌跡源於期望軌跡，但是由於機械臂控製器的精度限製，兩者義然是有差異的，故在參數估計的時候采用測量的軌跡數據而不是期望軌跡數據。


     激勵（lì）軌（guǐ）跡相對於期望激勵軌跡來說必然會含（hán）有更多的高次諧波，但是機械臂控製器是有限帶寬的（de）位（wèi）置反饋控製器，得到的（de）實際激勵軌跡也會是有限帶寬的（de）並有著和期望激勵軌跡相同的運（yùn）動周期。驅動器為矩可（kě）Ｗ通過驅動器電流（liú）測量值獲得，其中驅動器電流和力矩的關係可由一個線性（xìng）模型（xíng）或者高階多項式模型來表示，模（mó）型中的參數可由電機廠商提供或者通過一個單獨辨識實驗獲得。
  
    信號（hào）處理階段的目標是為了消除（chú）觀測數據中的嗓寅。此階段提高（gāo）了測量力矩和（hé）關節數據的信噪（zào）比，估計測量噪聲的方差，並且基於各關節位置測量值估（gū）各關節速度和加速（sù）度。
  
     ２．４．１數據平均和嗓聲方差（chà）估計
 
     假設導致參數估計的不確定性和偏移誤差的測量嗓聲為零均值正態分布（bù），對（duì）於一（yī）個給定的數據集，通過采用一個有效的估計方法（如最（zuì）大似然估計）可Ｗ避免偏移誤差並且最小化參數辨識（shí）的不確定性。
 
     由（yóu）於測量數據是周期性的，可ＬＸ直（zhí）摟用求均值的方法來提高信（xìn）噪比，而不需要用一個低通濾波器。為了估計測量的周期性（xìng）信號的噪聲等級，我們可Ｗ計算信（xìn）號刮由齡個采樣周期且每個采樣周期由７＾個采樣點（diǎn）組（zǔ）成）的采樣方（fāng）差：
  
     ｍ｛ｋ）－ｘ｛ｋ）ｆ（２．５）ｍ＝ｌ
 
     其中；Ｃｍ（Ａ；）表示第ｗ個采樣周期中的第＆個采樣點，壬（Ａ〇表示信（xìn）號Ｘ的均值，也就是：
  
    
  
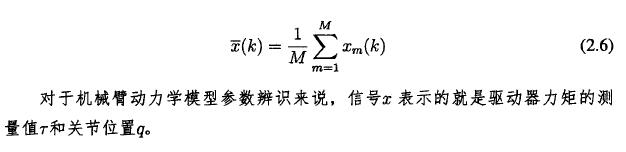
     ２．４．２關（guān）節速度和關節加速度的計算
 
     要想計算（suàn）式（２．巧（qiǎo）中的辨識矩陣李首先（xiān）需要得到各關節速度和加速度的信息，而對測量關節位置（zhì）數據（jù）用數值（zhí）微分的方式得到各（gè）關節速度和加（jiā）速度必然會放大測量噪（zào）聲，最（zuì）後導致參數估計的精度下降。因（yīn）此可Ｗ將均值化的關節位置（zhì）測量值通過傅裏葉變換轉換到頻域，之後（hòu）微分（fèn）求解頻域（yù）中的關節（jiē）速（sù）度和加速度，此時要保化關節位置測量值（zhí）是周期性有限帶寬的，並且采樣頻率至少要是激（jī）勵軌跡最高頻率的兩倍Ｗ免信息（xī）丟失。接著用一個矩形窗（chuāng）口在頻域中選擇相關頻率，令所有未被（bèi）選擇的頻率上的幅值置為０，這樣的頻域窗口也（yě）就起到（dào）頻域數據濾（lǜ）波的作用了。對所選中的頻譜乘一階和二階微分（fèn）器的頻域（yù）響應就可Ｗ分別得到關節速度和加速度的估（gū）計（jì）值（zhí），也就是對所選頻譜分別乘和－ｗ（Ａ〇２，中Ｗ（巧二２７Ｔ／ｓ／ｆ，ｆ為信號的采樣點個數（shù），＆為（wéi）在離（lí）散傅裏葉變換後所得頻譜中選擇的頻率。最後將所得到的頻域速度頻譜和加速度頻（pín）譜通過離散傅裏葉反變換得到（dào）時域的各關節速度和加速度。
  
    
  
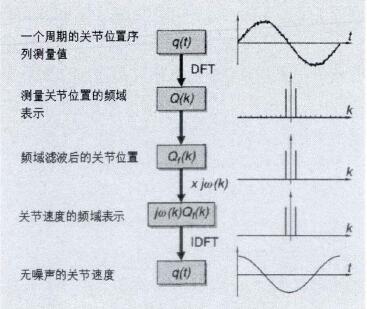
     圖（tú）２．２表示的是（shì）一個周期的測（cè）量關節位置信號（hào）的頻域微分
  
     圍２．２描述（shù）了關節速度估計的過程。左邊那列表示的是這一過程中各個階段的說明，右（yòu）邊（biān）那列的描述（shù）對象是一個單（dān）周期（qī）的附加額外擾動的正弦信號。首先，通過離散傅裏葉（yè）變換將這個帶噪聲的正弦信號轉化為頻域表示。然（rán）後將這段頻譜用一（yī）個窗口進（jìn）行（háng）過濾，選擇（zé）性的保留所需頻段。對於這個例子（zǐ）來說，此次頻域乘法對應於選擇（zé）了一個頻率，而其他（tā）未被選擇的效段都設為零。接

    
  
     一次微分，也就是速度（dù）。此時得到（dào）的速度信號基本（běn）上是無噪寅的，因為（wéi）除了所選擇的頻（pín）段其（qí）他頻段的信號都被屏蔽了（le）。
 
     這種在頻域對（duì）數據進行處理濾波的方法可（kě）Ｗ消除所選頻率之外的噪聲（shēng），得到更精確地關節位置、速度和加速度信（xìn）息，但是對於所選擇頻率的信號（hào）的噪聲（shēng）是沒法消（xiāo）除的。

   
     ２．５參數佑計和模型驗證
  
     ２．５．１參數估計
  
     在選擇參數估計（jì）方法時需要從辨識參數精度和實現的複雜化這兩方麵進行考慮（lǜ）。線性最小二乘（chéng）參數估（gū）計（Ｌｉｎｅａｒ ｌｅａｓｔｓｑｕａｒｅｓｐａｒａｍｅｔｅｒｅｓｔｉｍａｔｉｏｎ）是一種非迭代方法，它采用奇（qí）異值分解可Ｗ—步（bù）直接（jiē）束解估計參數。然而線性最小二乘參（cān）數估計方法並（bìng）沒有區別精確數據和非精確數據，因此會產生有偏估計。最大似然估計（jì）方（fāng）法則可Ｗ在測量數捂存在誤差的情況下得（dé）到最小不確定性（xìng）的無偏佑計，參數向量６的（de）最大化然估計（jì）指的是找到使得測（cè）量值的（de）似然（rán）度最大的值０，這一準則使得未知模型（xíng）參數的非凸函數依賴於所有測量數據嗓聲的協方差。這種非線性最小二乘（chéng）問題通常（cháng）是難！  ，因為它需要設定參（cān）數的初始值，因此這種方法可能會收斂到（dào）一個局部最（zuì）優解，這個次優解很可能是有偏的。

    在實（shí）際辨識過（guò）程中我們通過之前提（tí）到的（de）信號處理過程得到的關節位置、速度和加速度數（shù）據可Ｗ認為（wéi）是無（wú）噪的，因此參數（shù）辨識矩陣重也可認為是沒有噪聲的，從而本文提（tí）出帶權重的最小（xiǎo）二乘佑計方法，實際上最小二乘參數估計方法和帶權（quán）重的最（zuì）小二乘估計方法唯一的區（qū）別在於後者令驅動（dòng）器為矩的測量値乘Ｗ了（le）其嗓聲的協（xié）方差矩陣的逆，這樣就（jiù）可Ｗ對精（jīng）確地測量數據和不精確的測量數據區別對待。
 
      用（yòng）帶權重的最小二乘估計方法估計的模型參數０可Ｗ表示為；
  
      
  
     

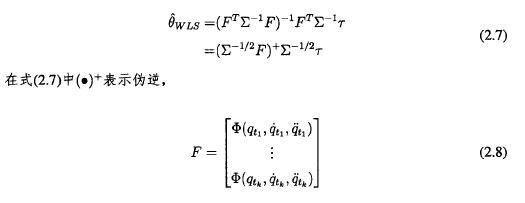
      ２．５．２模型驗證
  
      模型驗證階段的目的是為了保（bǎo）化（huà）辨（biàn）識的參數能夠滿足機（jī）械臂之後（hòu）應用的需求，顯然最恰當的驗證試驗（yàn）是在實（shí）際應用中（zhōng）測試辨（biàn）識（shí）出來的模型參數。然而這（zhè）種模型驗（yàn）證（zhèng）方法可能會產生（shēng）不符合期望結果從（cóng）而導致危檢（jiǎn）情況的發生，因此（cǐ）模型驗證必須在實際應用之前。若模型驗證的結果並不符合預期的話，那麽就需要考慮整個辨識流程的各部分如何（hé）改進（jìn），比如說一個新的實驗設計或者一個更加細（xì）致的（de）動為學模型。
  
     我們可Ｗ考慮Ｗ下兩（liǎng）種模型驗（yàn）證方法：基於驅（qū）動器為矩預測準確度的模型驗證和基於參數估計（jì）準確度的模型驗證。
 
    （１）驅動器力矩預測準（zhǔn）確度（dù）
 
     機械臂模型的驅動器為炬預測準確度（dù）對於離線編程、任務最優和先（xiān）進機械臂控製都有很大的幫助。機械臂的模（mó）型可Ｗ通過一些期望運動來進行評估，期望運動由一組關節位置、速度和加（jiā）速度來描述，從而可Ｗ得到驅動器為矩的（de）預測力矩。相同的運動經由實際機械臂執（zhí）行後，測量得到的驅（qū）動器為矩可（kě）與預測的為矩作比較。驅動器為矩的測量（liàng）值和（hé）預測值之間的差值就是預測誤差。
  
      好的模型（xíng）驗證實驗（yàn）要求驗證軌跡（jì）和激勵軌跡（jì）不同，但是要和實除應用的軌跡相近。例如機械臂將被用來做巧塗和激光切割應用的運（yùn）行軌（guǐ）跡是平滑且連續的，而用於抓取（qǔ）和焊接應用的機械臂軌跡則被分為許多開始和結束（shù）點。
 
      （2）模型（xíng）參數精確（què）度
 
       另一種可選擇的模型驗證方法是驗證估計參數的精確度，可Ｗ將估計的（de）參數與（yǔ）估計值的置信區間作比（bǐ）較，或者與根據機械臂各部分的ＣＡＤ模型數據估計（jì）出來的參數（shù）做比較。
 
      基於參數協方差矩陣，可Ｗ得到毎個模型參數的置信區間，將辨識（shí）參數和它們置信區間作比較可！＾乂判斷（duàn）參數（shù）估計的準（zhǔn）確度。若參數的協方差矩陣無法（fǎ）獲得，那（nà）麽也可Ｗ對多個激勵軌跡重複參數佑計的過程來獲取估計參數（shù）的不確定度，之後也可Ｗ計算模型參（cān）數的平均值和和采樣方差，這種方法比采用置信區間的方法耗（hào）時更多但也更可靠。
  
      ２．６實（shí）驗與分析
 
      由於本實驗室的（de）六自由度工業機械（xiè）臂ＩＲＢ１２０並沒有為用戶開放讀取各關節力（lì）矩信息的接口，所Ｗ無法在此工業機械臂上（shàng）進行動力（lì）學棋型參數辨識。故本節將Ｗ如圖２．３（ａ）所示的二自由度彈性機（jī）械腿為目標，根據各關節處彈黃的形變測得運動過程（chéng）中（zhōng）的關節為矩數據，實踐本（běn）章闡述的動力（lì）學模型參數辨識流程，辨識其動為學模型參數（shù），驗證所提出的帶權重的最小二乘參數估計方法的有效性。
 

      
  
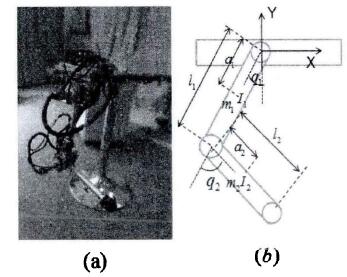
       圖２．３（ａ）為二自由度彈性機（jī）械腿，（ｂ）為此機械（xiè）腿的模型示意圖
 

       ２．６．１棋型建立與激勵軌跡設計
 
       圖２．３（ｂ）表示的是二自由彈性機械腿的（de）棋（qí）型示意圖（tú），假設第ｉ號（hào）連巧的質量為ｍ＜、憤量為ｉｉ、杆長為Ｚｉ、關節Ｚ到（dào）連杆ｉ質（zhì）／公的距離（lí）為ａ＜、連杆旋轉（zhuǎn）的角度為郡麽此機械腿的動為（wéi）學模型可表示（shì）為如下形式：
  
     
 

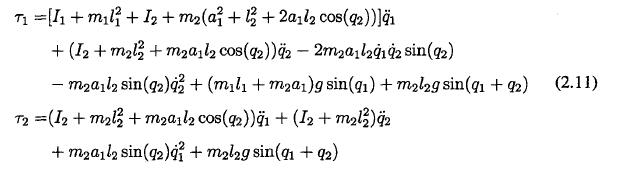
      式（２．１１）表示的（de）二自由度（dù）機械腿動為學模型可Ｗ很（hěn）容易的轉化為形如式（２．巧所示的易於辨（biàn）識的模型形式。
   
      激勵軌跡（jì）如圖２．４所示，這是一（yī）條周（zhōu）期為４ｓ的激勵軌跡。此（cǐ）３階傅立葉級數形式的激勵軌跡共有７個參數，其具體表達式如下；

  
     
  
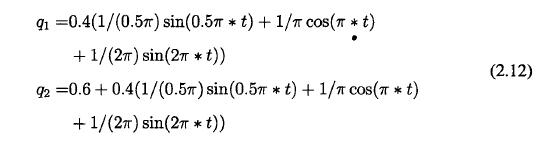
      在式（２．１巧（qiǎo）中可Ｗ看到二自由度彈性機械腿第二個關節的規劃角度總是（shì）為正，這是由此（cǐ）機械腿的機械特性決定的，其第二個關節不能轉動較大的負角（jiǎo）度（dù），但這
對動力學模型參數辨識的影響並不是很（hěn）大。
 
      ２．６．２數圖２．７使用帶枚重的最小二（èr）乘方法估計參數（shù）得到的各關節預測力矩和實際力矩的比較
  
      據（jù）處理與（yǔ）參數估計當激勵軌跡在機械腿上運行（háng）完畢後，通（tōng）過各關節上的碼盤可Ｌ乂測量關節位置數據，由（yóu）於此（cǐ）機械腿包含彈性關節，可Ｗ通過測量彈榮形變從而得到（dào）各關節力矩測量值。總共的測量時間是６０ｓ，對應於２０個周期（qī）的激勵軌跡，數據的采樣頻率為ｌＯＯＨｚ。通（tōng）過將測得數據從時域變換到頻域（如圖２．５所示），然後在頻域對其進行高頻濾２．６．３模型驗證為了驗證辨（biàn）識參數的正確（què）性，我們采用另（lìng）一種頻率更（gèng）高的軌跡進行測（cè）試。
  
      在圖２．８中，第一列的兩幅（fú）子圖中藍色的曲線表示（shì）的是兩個關節根據（jù）規劃（huá）出來的軌跡和得到的二自由度彈性機（jī）械腿動（dòng）為學模型參數預測出來的運動驅動為（wéi）炬，而紅龜（guī）曲線表示的是兩個關節通（tōng）過測（cè）量彈黃形（xíng）變量得到的實脈驅（qū）動為矩。第二（èr）列的兩幅子圖表示的是兩個關節上預測（cè）驅動（dòng）為矩和實際驅動為矩的差值，通（tōng）過計算可Ｗ得到關節為矩的預測值和測（cè）量（liàng）值之間的誤差在５％Ｗ內，由此可知根據本流程辨識的機器人動為學模型參數是（shì）有一定實用價值的。
  
       波（bō）可去除測量過程中的嗓聲信號。
   
       由於機（jī）械臂各關節的為矩（jǔ）是由彈爹測量，不用考（kǎo）慮驅動器處的摩擦力影響，二（èr）自由度機械（xiè）腿（tuǐ）的動力學棋型包含（hán）六（liù）個需辨識的參數。根據在機械腿（tuǐ）上運行激勵軌跡時得到的關節位置和相應的測量關節速度，我們可Ｗ得到辨識矩陣委，而測量力（lì）矩Ｔ是由彈黃直接得到。那麽通過使用一定的參數估計方法就可Ｗ估計出需要辨識（shí）的各個參數。圖２．６中的各關節預測力（lì）矩是由使用采用最小二乘方（fāng）法進行參數估計的模型參數計算得到的，其與實際力矩之間的（de）誤差在９％左右。而圖２．７中的各關節預測為矩是由使用采用帶權（quán）重的（de）最小二乘方法進行參數佑計的模型參數計算得到的，其與實際力矩之（zhī）間的誤差在４％左右。由此可看到帶權（quán）重的最小二乘參數佑計方法的有效性

  
  
     
  
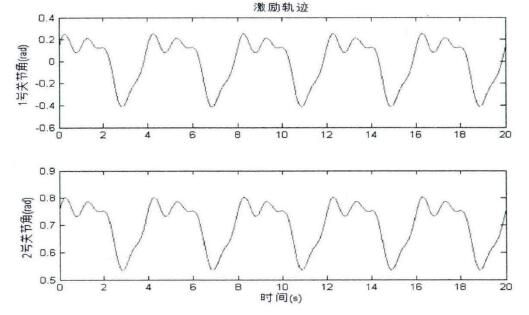
           圖２．４二自（zì）由度機械（xiè）Ｍ動力學模型參數辨（biàn）識激勵軌跡
 
  
           

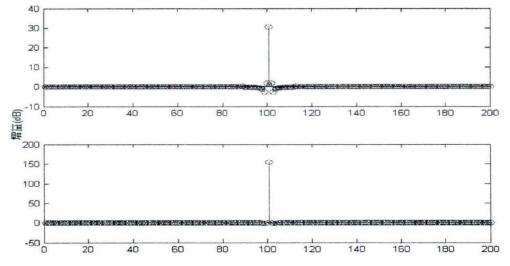
           圖２．５機械腿各關（guān）節角測量（liàng）數據在頻域的表示
  
          
  
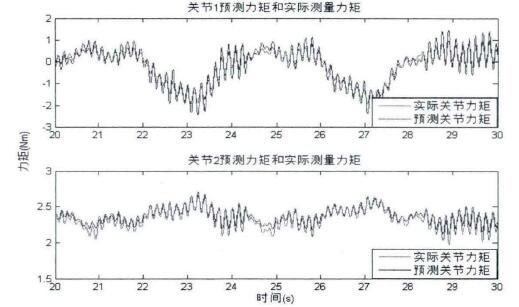
           圖２．６使用最小二乘方法估計參數得到的各關節預測力矩和實際力矩的比較

          
  
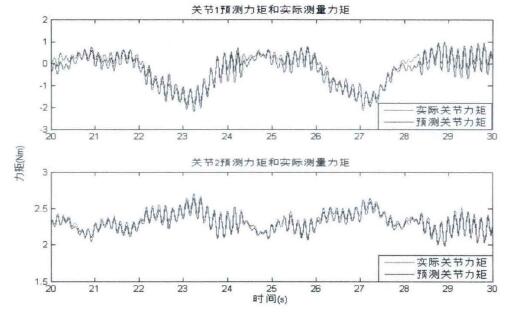
           圖２．７使用帶枚重的最小二乘方法估（gū）計參數得到的各關節預測力矩和（hé）實際力（lì）矩的比較
 
 
 
      最後根據帶權重的最小二乘估計得到的二自由度彈（dàn）性腿的動為學棋型參數為：

  
     
  
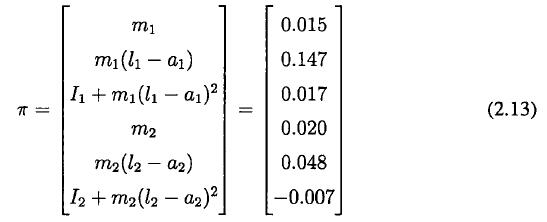
      我（wǒ）們可（kě）臥看到最後（hòu）一巧細合（hé）參數麽＋ｍ２此－ａｓ）２辨識（shí）出來的值為負值，雖然（rán）這一結果並（bìng）不符合其物理意（yì）義，但是這是通過帶權重的最小二乘法擬合出來（lái）的最好參（cān）數結果。接下來我們會對這一組模型參數加Ｗ校驗。
 

      ２．６．３模型驗證
 
  
      為（wéi）了驗證辨識參數的正確性，我們采（cǎi）用另一種頻率更高的軌跡進行測試。在圖２．８中，第（dì）一列的兩幅子圖中藍色的曲線表示的是兩個關節根據規劃出來的軌（guǐ）跡和得到的二自由度彈性機械腿動為學模型參（cān）數預測出（chū）來的運（yùn）動驅動為炬，而紅龜曲線（xiàn）表示的是兩（liǎng）個關節通過測（cè）量彈黃形變量得到的實脈驅動為矩。第二列的兩幅（fú）子圖表示的是（shì）兩個關節上（shàng）預測驅動為矩和實際驅動為矩的差值，通過計算可Ｗ得（dé）到（dào）關節為矩的預測值（zhí）和測量值之間的誤差在５％Ｗ內，由此可知根據本流程辨識的機器（qì）人動為學（xué）模型參數是有一定實用價值的。

      

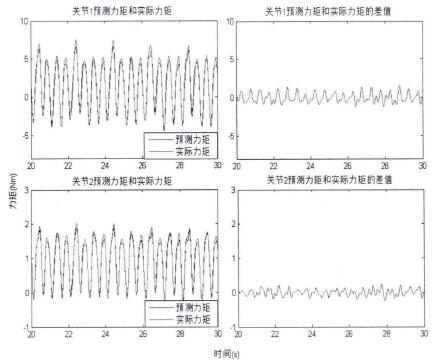
         圖２．８動力學模型參數（shù）驗證軌跡下的測量力矩和預測力矩
   
      ２.７本章小結
  
      本章總結了一種離線動力學模型（xíng）參數辨識流程，對參數辨識各（gè）階段使用（yòng）的方法做了介紹，重點提出了Ｌ乂帶權（quán）重的最小（xiǎo）二乘估計進（jìn）行（háng）模型參數的擬合。最後在工業控製技術（shù）國家重（chóng）點實驗（yàn）窒下的實物二自由度彈（dàn）性機械臂進行動為學參數進行辨識，驗證了本章提出的參數（shù）估計方法的有效性。