航空發動機雙轉子係統的(de)模態分析
2014-1-9 來源:數控機床市場網 作者:申(shēn)苗 唐駕時 李克安 梁翠香 陳勇 隋雪
摘要:為了(le)更好地了解和掌握發動機固有的振動特性,利用有限元分(fèn)析 ANSYS 軟件,對某型發動機雙轉子係(xì)統進行了固有頻率及振型計算。通過(guò)改變軸承的剛度與原計算結果(guǒ)作對比,分析軸承(chéng)剛度的(de)改變對整個係統動力特(tè)性的影響。結合振動力學相關(guān)理論,對設計方案進(jìn)行動力學(xué)評價。結果表明,該方法運算速度快,輸入參數少,特征值、特征向(xiàng)量求解精度高。
關鍵詞:雙轉子;有限元方法;模態分析
1 引言
航空發動機(jī)的結構複雜,在工作中會(huì)受到機械激振、氣動激振等作用,使振動(dòng)問(wèn)題突(tū)出。機械振動產生破壞主(zhǔ)要因共振引起,當激振頻率與係統的(de)某階固有頻率接(jiē)近時,振幅會急劇增大,從而(ér)產生嚴重後果。因此,各階固有頻率和振型是(shì)結構承受動力荷載設計中的重要參數,所以必須對發動機的動力學特性進行研究(jiū)。目前,對航空發動機轉子(zǐ)係統的研究(jiū)集中在相對簡單的單(dān)轉子(zǐ)係統上,對複雜的雙轉子係統研究得很少。大型有限元分析軟件ANSYS[5-8]是結構動力學分析常(cháng)用的軟件。故利(lì)用ANSYS計算了某(mǒu)型發動機(jī)雙(shuāng)轉(zhuǎn)子係統的固有頻率和振型,研究軸承(chéng)剛度的改變(biàn)對係統動力特性的影響,並結(jié)合其工況對設計方案進行動力學評價。
1 雙轉子係統有限元分析(xī)模型的建立
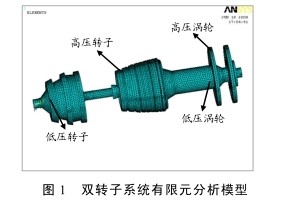
雙轉子係統具有(yǒu)傳統的盤鼓結構,在各級盤上附有發動(dòng)機的葉片。係統(tǒng)由(yóu)低(dī)壓轉子和高壓轉子組成。低壓轉子主要包括低壓壓氣機、低壓渦淪。高壓(yā)轉子主要包括高壓壓氣機(jī)、高壓渦淪。高低壓轉子間通過 2 個滾動軸間(jiān)軸承連接。整個係統又通過多個軸承與外部的靜子(zǐ)機匣相連。航空發動機的轉子係統非常複(fù)雜,影響轉子(zǐ)動力特性的因素也很多,在建模過程中關鍵是要考慮各種主要因素的影響。針對轉子(zǐ)的結構特點,確定建模方案如下(xià):
1) 質量是(shì)影響(xiǎng)固(gù)有頻率的主要因素之一,因此(cǐ),建模時應盡可能地接近實物模型的實際尺寸,但(dàn)一些細小的結構如倒角、螺孔(kǒng)可以忽略。主要部件的材(cái)料參數也盡量保持與(yǔ)實際情況相符。
2) 軸承(chéng)隻考慮徑向剛度,剛度值取測試得到的靜剛度值。軸承在 ANSYS 中用彈簧模擬。
3) 考慮到葉片的顫振對模態分析結果的影響(xiǎng),將各級葉片按質量等效到各(gè)級盤上。為使模型盡可能精確,采用 ANSYS 對其進行三(sān)維實體建模,模型主要采(cǎi)用 SOLID45 單(dān)元建(jiàn)立。 再對各(gè)個(gè)部件定義材料屬性劃(huá)分網格,將軸承簡化為彈簧作(zuò)為邊(biān)界條件施加(jiā)於模型上,2 個軸間軸承簡(jiǎn)化得到的彈簧連接高(gāo)低壓軸,與(yǔ)機匣相連的軸承(chéng)簡化得到的彈簧一端與雙轉子係統相連,另(lìng)一端固(gù)支,軸承剛度均使用靜剛度。得到有限元分析模型如圖 1。
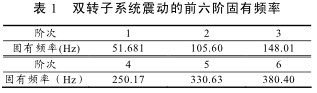
2 模態計(jì)算與分析(xī)
采用子空間法(Subspace)計算雙轉子係統的模態,該方法運算速度快(kuài),輸入參數少,特征(zhēng)值、特(tè)征向量求解精度高。由振動理論可知(zhī),對於一個多自由度振動係統,係統低階固有頻率就能反(fǎn)映係統的動態特(tè)性。在雙(shuāng)轉子係(xì)統的(de)振動中,低階模態起主導作用,高階模態的影響較小。計算得雙轉子係統的前六階(jiē)固有頻率如表 1,相應(yīng)的振型如圖 2。
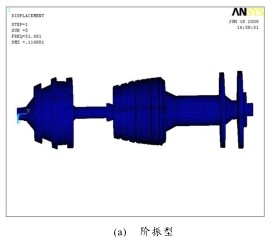
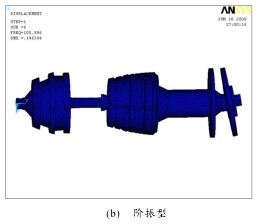
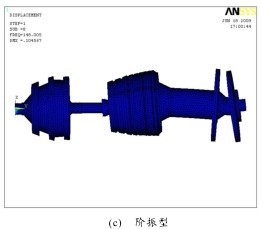
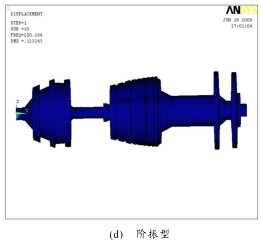
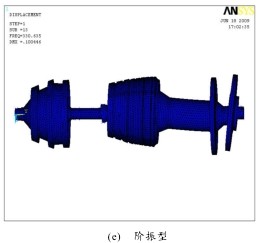
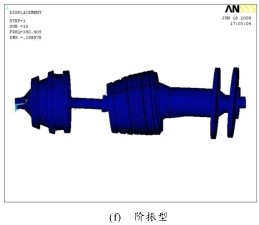
圖 2 振型圖
分析計算固有頻率和(hé)相應的振型,結論如下:
1) 模態計算的結果與(yǔ)試驗結果相(xiàng)符合。
2) 當外(wài)部(bù)激勵的頻率接(jiē)近表 1 中數值時,會產生較大(dà)振幅,使結構受到損害,因此,必須通過修改設計,改變共振出現的頻率範圍,以提高發動機(jī)運行過程的平(píng)穩性。
3) 第 1、4 階固(gù)有振型主要是扭轉振動,其中,第 1 階主要是低壓轉子的扭振;第 4 階主要是高壓(yā)轉子的扭振。第 2、5、6 階固有振型主要是垂直麵內(nèi)的彎振(zhèn),其中,第 2 階主要是低渦盤和高壓壓氣機在垂直麵內的彎振,高壓壓氣(qì)機的振幅(fú)相(xiàng)對較小;第 5 階主要是高壓壓氣機和 2 個渦輪盤在垂直麵內的彎振,低壓壓氣機也有相(xiàng)對很小的振動;第 6 階是整個(gè)雙轉子係統在垂直麵內的彎振。第 3 階固有振型主要是高壓壓氣機和 2 個渦輪(lún)盤在水平麵內的彎(wān)振,低壓壓氣機也有相(xiàng)對很小的振動。
4) 前四階固(gù)有頻率雖(suī)然出現的可能性大,但頻(pín)率值低,遠遠沒達到雙轉子係統的共振頻率,後兩階固有(yǒu)頻率值相對比(bǐ)較接近係統(tǒng)的共振頻(pín)率,但由於階數高(gāo),出(chū)現的可能性不大。
3 軸承剛度變化對模態分析(xī)的影響
轉子高速運(yùn)轉時,軸承的剛度發生改變,故要考慮軸承的動剛度。目前,還沒有可(kě)靠的方法來得到準確的軸承動剛度值,故計算(suàn)時用增大和縮小靜剛度值來分析軸承剛度(dù)對模態計算的影響。將軸承(chéng)剛度值減小 20% 和增加 20%,計算雙轉子係統的(de)前六階固有頻率,結果如表 2(其中 B 組為對照組)。
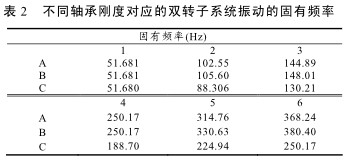
1) 若轉子高速運轉時,軸承的(de)剛度值縮小了,從(cóng)表(biǎo) 2 中可以看出,雙轉子係統振動的(de)固有頻(pín)率均變小(xiǎo)了,第 1、4 階扭振不(bú)受影響。第 5、6 階固有頻率改(gǎi)變較(jiào)大,第 2、3 階固有頻率變化(huà)不大。
2) 轉子(zǐ)高速運轉(zhuǎn)時軸承的(de)剛度值增大,從表 2中可以看(kàn)出,第 1 階扭振頻率大小不受影響。第 2、3、4、5、6 階固有頻率變小了,第 2 階扭振的出現由原來的總體階數第4階推遲到總體階(jiē)數的第6階。
3) 該結果能用來(lái)間接地分析軸承動剛度對雙(shuāng)轉子係統振(zhèn)動固(gù)有頻(pín)率(lǜ)的影(yǐng)響,定性地研究軸承剛度的改變使雙(shuāng)轉子係統振動特性發生(shēng)的(de)變化(huà)。
4 結論
1) 建模時,使用簡化方案,且模型主要(yào)采用三維 SOLID45 單元,使(shǐ)得(dé)模型更接近於實物(wù),為對雙轉(zhuǎn)子係統進(jìn)行準確的模態分(fèn)析提供了有力的保(bǎo)證。
2) 在使用軸承(chéng)靜剛度時, 得到前四階固有頻率值較(jiào)小,故在發動機啟動速度推進時,就盡(jìn)量地在這些頻率對應的轉速處迅速推(tuī)過,達到避開共振的(de)效果,使雙(shuāng)轉子係統迅速進入穩定工作狀態。而後兩階固有頻率對應(yīng)的臨界轉(zhuǎn)速雖然比較接近發動(dòng)機的轉速,但因是高階(jiē)頻率,故出現(xiàn)的可能性極小。
3) 改變軸承的剛度值(zhí)會引起雙轉子係統固有頻率的(de)變化,故當臨界轉速接近或處於工作區域時,可通過改變軸承的(de)剛度來降低或提高係統的(de)固有頻率,使臨界轉速避開工作區域。可定性地研究軸承剛度的(de)改變對雙轉子(zǐ)係統(tǒng)振動特性(xìng)的影響。轉子高速運轉時,軸承的剛度會改變,在還沒有一種(zhǒng)可靠的方法來得到準確的軸承動剛度值(zhí)之前,可(kě)以考慮用增大和(hé)縮(suō)小靜剛度值來(lái)近似模擬動(dòng)剛度值,並將計算結果作為轉子(zǐ)高(gāo)速運轉時的動力特性的參考。
投稿箱:
如果您有機床行(háng)業、企業相關(guān)新聞稿(gǎo)件發表(biǎo),或進行資訊合作,歡迎(yíng)聯係本網編輯部, 郵箱(xiāng):skjcsc@vip.sina.com
如果您有機床行(háng)業、企業相關(guān)新聞稿(gǎo)件發表(biǎo),或進行資訊合作,歡迎(yíng)聯係本網編輯部, 郵箱(xiāng):skjcsc@vip.sina.com
更多相關信息
業界視(shì)點
| 更(gèng)多
行業數據
| 更多
- 2024年11月 金屬切削機床產量數據(jù)
- 2024年11月(yuè) 分地區金屬切削機(jī)床產量數據
- 2024年11月 軸承出口情況
- 2024年11月 基本型乘用車(轎車)產量數(shù)據
- 2024年(nián)11月 新能源汽車產量數據
- 2024年11月 新能源汽車銷量情況
- 2024年10月 新能源汽車產量數據
- 2024年10月 軸承出口情況
- 2024年10月 分地區金屬切削機床產量數據
- 2024年10月 金(jīn)屬切削機床產量數據
- 2024年9月 新能源汽車(chē)銷量情況
- 2024年8月 新能源汽車產量數據
- 2028年8月 基(jī)本型乘用車(轎車)產量(liàng)數據





