機床主軸熱誤差的累積法建模研究
2017-8-3 來源:南通大學 機械工程學院 作者:袁 江,周成一,邱自學,沈亞峰,邵建新
摘要: 為實現數控機床熱誤差的快(kuài)速(sù)精確建模,提(tí)出一種基於累積法的機床熱(rè)誤(wù)差建模新方法。對一台立式加工中心,利用溫(wēn)度傳感器與非接觸式(shì)激光位移傳感器(qì)同步測量主軸溫(wēn)度(dù)變(biàn)化及熱變形值,對(duì)獲取的模型數據進行累(lèi)積算子求和,構建累積矩陣及熱誤差(chà)正規方程來估計模型中的(de)參數以實現熱誤差建模。利用該方法構(gòu)建(jiàn)的熱誤差模型分別與最小二乘(chéng)法( S) 、最小二乘支持向量機( LS-SVM) 模型進行對(duì)比,結(jié)果表明: 累積法的建模精度要高於最小二乘(chéng)法,且建模時間比最小二乘支持向量機法要少。
關鍵詞: 累積法; 主軸; 熱誤差; 建模
0.引言
隨著機床製造水平的迅猛發展,溫升引起的熱誤差已成為影響機床加工精度(dù)的主(zhǔ)要問題[1-2]。由於機床熱誤差具有非(fēi)線性、交互性和耦合性等特點(diǎn),傳統的基於最(zuì)小二乘原(yuán)理的(de)建模方法雖建模簡單,但模型(xíng)魯棒性差,難(nán)以實(shí)現數控機床熱誤差高精度補償[3-4]; 近年來,國內外學者提出了神經網絡、灰色理論、最小二乘支持向量機等多種熱誤差建模方法,但也存在一定的局限性,例如(rú)神經網絡以及最小二乘支持向量機等建(jiàn)模方法雖可以將補償(cháng)精(jīng)度提高數倍,但需大量的樣本進行訓練、建(jiàn)模複雜,且神經網絡還易產生過學習(xí)或欠學習等問題; 灰色理論(lùn)預測等(děng)則對建(jiàn)模誤差數據光滑(huá)性有嚴格要求,模型適應性不好[5-8],因此還需要尋求快速、高精度的建模(mó)方法。累積法是 1778 年由意大利數學家馬爾奇西提出,但直至我國(guó)曹定愛教授在 1985 年創造性地提出(chū)累積(jī)算子的各階通式,才從本質上簡化了累積法的(de)計(jì)算,使其在工程投資(zī)預算、建築材(cái)料(liào)參(cān)數估計、彈道測量數據處理(lǐ)等方麵得到了廣泛應用[9]。累積法最大的特點是不直接處理誤差項,用有規可循的累積(jī)和來估計模型參數,具有簡單、直觀、便於計算機實現等突出優點。本文(wén)將其運(yùn)用到機床熱誤差建(jiàn)模領域,並與最小二乘法和最小二乘支持向量機兩種建模方法進行了對比分析。
1.累積法建模
1. 1 累積和




1. 3 參數估(gū)計
由樣本(běn)的 k 階(jiē)累積和及累(lèi)積廣義(yì)均值將正規方程
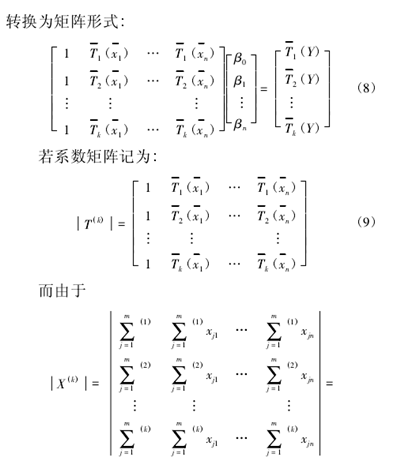
2.熱誤差(chà)實(shí)驗建模及對比
2. 1 熱誤差實驗
選取一台 VMC1060 數控機床為被測對象,經過前期研究,采用熱敏區域黃金分割法對(duì)機床主軸測溫點進行(háng)優化,並得出最佳測溫區域為[54mm,84mm],考慮到傳感器直徑及現場布置,在此區域內(nèi)布(bù)置兩個測點,並將激光位移(yí)傳感器安裝(zhuāng)於主軸端麵軸(zhóu)中心延長線上,以監測主軸軸向熱位移的(de)變化(huà)[11]。其中,溫度傳感器采集的溫度信息通過無線發送器發送給接收(shōu)器,接收器再將信號通過 RS232-USB 轉(zhuǎn)接口傳(chuán)輸給上位機,實現無線信號的采集與處理,避免了傳統有線測試方法的(de)布線(xiàn)難、維護(hù)困難等問(wèn)題; 而激光位移傳感器則(zé)通過專用的控製器連接上位機,實(shí)現(xiàn)熱位移信息的采集傳輸; 上位機對溫度傳感器(qì)及激光位移傳感器同步(bù)發送命令,並將接收的溫度、熱位移信息實時顯示存儲。

圖 1 累積法建模流程圖
測(cè)試時,每隔 3min 采(cǎi)集(jí)一次各測(cè)點溫度 x 和熱位移 y,共采集 43 組數(shù)據。現場測試及(jí)結果分別如圖 2、圖 3 所示。

圖 2 現場測試圖
2. 2 熱誤差建模
構建熱誤差(chà)回歸模型之前需(xū)要確定(dìng)累積(jī)矩陣階(jiē)數(shù)k 和熱誤差樣本容量 m,由於本熱誤差實驗選取兩個熱敏測點進行測試,即熱誤差方程的自變(biàn)量為溫度 x1和溫度 x2,且各含有 43 組數據,因此有:
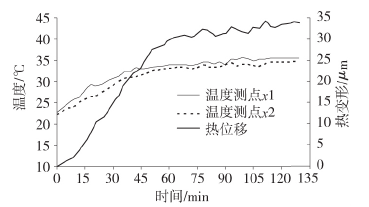
圖 3 熱誤差(chà)測試結果


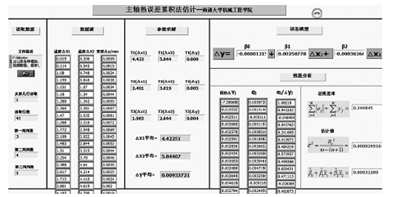
圖 4 累積法建模(mó)結果

2. 3 建模精度對比分析
國內外(wài)許多學者雖提出了諸如灰色理論、神經網絡、最小二乘(chéng)支持向量機等多種熱誤差建模方法,但最小(xiǎo)二乘法憑借其(qí)建模簡便、高效等優點,仍是用於回歸分析的一種經典方法; 而最小二(èr)乘支持向量機( LS-SVM) 不僅保持(chí)了支持向量機建模精度(dù)高(gāo)、穩健性(xìng)好的(de)優點,並(bìng)且經過適當的變換簡化了運算算法,降低了運算成(chéng)本[13]。本文分別采用累積(jī)法、最小二乘法( LS) 和最小二乘支持向量機法( LS-SVM) 對熱誤(wù)差測量數(shù)據進行回歸方程預測,並對比分析。各模型預測值與實際值對(duì)比效果如圖 5 所示,各模型預測殘差如圖 6 所示。此外(wài),采用平均絕對百(bǎi)分(fèn)比誤差( MAPE) 及總參差率作為(wéi)模型精度評價指標,結果如表 1 所示。其中 MAPE和(hé)總殘差率計(jì)算公式(shì)分別為:
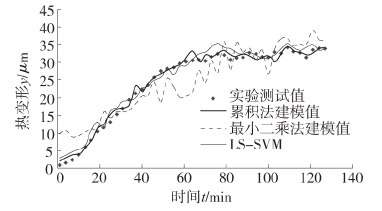
圖 5 各模型(xíng)預測值(zhí)與實際測量值對比效果
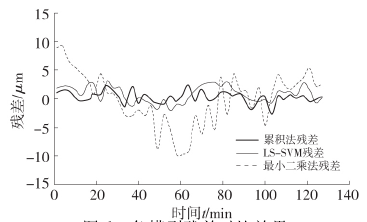
圖 6 各模型殘(cán)差(chà)對比效果
表 1 建模精度對比結(jié)果
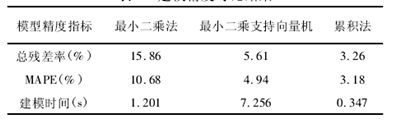
由上述結果(guǒ)可以看出,累積法與 LS-SVM 法的總(zǒng)殘差率及總百分比誤差指標相當(dāng),精度(dù)均高於最小二(èr)乘法,但 LS-SVM 模型構建時間遠大於累積法。因此,累積法較傳統 LS 法及 LS-SVM 法不僅建模精度高,而且建模(mó)時間大大減少,更適用於(yú)熱誤(wù)差建模及(jí)後續的補償(cháng)應用。
3.結論
為提高熱誤差模型預測能力,提出了一種基於累積法的機床熱誤差建模方法,其在不處理(lǐ)誤(wù)差項的基礎上快速進行模型參數估計,估計量具有無偏、線性、有效、唯一等特點; 對 VMC1060 數控機床進行累積法熱誤差建模試驗,取(qǔ)得(dé)了良好的預測效果,同(tóng)時與 LS、LS-SVM 方法進行模型對比分析。結果表明,累積(jī)法模(mó)型總殘(cán)差率及(jí) MAPE 均在 3% 左右,建模時間低於0. 5s,三項指標均優於(yú)後兩種方法。
投(tóu)稿箱:
如果您有機床行業(yè)、企業相關新聞稿件發表,或進行資訊合(hé)作,歡(huān)迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業(yè)、企業相關新聞稿件發表,或進行資訊合(hé)作,歡(huān)迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息
業界視點
| 更多
行業數(shù)據
| 更多
- 2024年11月 金屬(shǔ)切(qiē)削機床產量(liàng)數據
- 2024年11月 分地區金屬切削機床產量數據
- 2024年11月 軸承出口情況
- 2024年11月 基本型乘用車(轎車)產量數(shù)據
- 2024年11月 新能源汽車產(chǎn)量數據
- 2024年11月(yuè) 新能源汽車銷量情(qíng)況
- 2024年10月 新能源汽車產量數據
- 2024年10月(yuè) 軸承出口情況
- 2024年10月 分地(dì)區金(jīn)屬切削機床產量數據
- 2024年10月 金屬切削機床產量數據
- 2024年9月 新能源汽車銷量情況
- 2024年8月 新能源汽車產量(liàng)數據
- 2028年8月 基本型乘用車(轎車(chē))產量數據




