數控滾齒機滾刀主軸振動特(tè)性(xìng)研究(下)
2018-10-15 來源:(重慶機(jī)床(集團)有(yǒu)限責任公司 作者:李先廣 楊勇
3、滾齒機滾刀主軸振動測(cè)試數據分析(xī)
通過(guò)對滾齒機滾刀主軸振動測試信號提出與分析,獲得主軸結(jié)構時域、頻域響應數據,並(bìng)根據振動加(jiā)速度(dù)數據(jù)獲得主軸 X 向振型或振動位移數據。為(wéi)了對表 1 與表 2 中理論數據進行對比(bǐ)分析,對應提取與分析(xī)了第 1、3 及 5 階振動測試響應特性數據曲線。
3.1 滾齒(chǐ)機主軸振(zhèn)動頻率響應分析
根(gēn)據滾刀主軸振動試(shì)驗信號,提取前 5 階振動頻率值、振動加速度及振動位(wèi)移響應特性數據。前5 階振(zhèn)動頻率(lǜ)值如(rú)表 4 所示。
表 4 滾刀主軸(zhóu)前 5 階振動頻率
由表 4 可知,滾(gǔn)刀(dāo)主軸前 5 階振動頻率,均大於或偏離滾刀主軸工作轉速對應諧次激振(zhèn)頻率(滾刀參數:單頭滾刀,槽數為 10;工作轉速 40 r/min對應一諧(xié)次頻率為: 1×(40×1×10)÷60=6.67 Hz,二諧次頻率為(wéi):2×(40×1×10)÷60=13.33 Hz,同理可(kě)得三諧次頻率為:20 Hz,四諧次頻率為:26.67 Hz,五諧次頻率為:33.33 Hz;通常情況下,滾齒機(jī)工作轉速遠低於最高轉速,則不考慮最高轉速對應激(jī)振頻率),表明主軸設計結構不會出現(xiàn)共振現象,剛度(dù)滿足工程設(shè)計要求,且有優化減重空間。
3.2 振動加速度響應分析
由(yóu)圖 8 可知,當滾齒(chǐ)機工件滾切(qiē)深度ht =45 mm,主軸(zhóu)轉速5n =40 r/min,且均固定不變時,滾刀主軸各階振動(dòng)加速度隨著滾齒時間均(jun1)呈等幅值周期性變化,滾刀主軸在 X 方(fāng)向出現(xiàn)左右擺振,表明滾齒加工中滾刀與工件的摩擦切削齧合,對滾刀主軸(zhóu)振動響應是(shì)以周期性動態激勵為主要影響。由圖8 有,滾刀主(zhǔ)軸第 1 階最大加速度幅值約為 66.8 m·s2,第 3 階最大加速度幅(fú)值約為 181.8 m·s2,第 5 階最大加速度幅值約為 184.5 m·s2。 根據表(biǎo) 2 與圖 8 可得,由滾刀主軸最大振動加速度幅值理論(lùn)模型計算與測試對比數據的表 5 可知,理論(lùn)與測試值間(jiān)的相對誤差(chà)均(jun1)小於 5%,即理論計算與測試值的一致性(xìng)較好,驗證了該型號滾齒機滾(gǔn)刀主軸振動加速度響應理(lǐ)論推導模型(xíng)的正確性(xìng),該方法為其他係列滾齒(chǐ)機主軸振動特性理論與試驗研究提供經驗借鑒與參考作用。 為了深入(rù)分析(xī)主軸振動特性,將主軸振動測試的加速(sù)度(dù)值與滾(gǔn)齒轉速建立了加速度-轉速關係曲線(xiàn)。由圖 9 可(kě)知,當滾切深度ht =45 mm 且固定不(bú)變時(shí),齒輪加工初期與低轉(zhuǎn)速情況下滾刀主軸振動加速度較大;並且隨著轉速與振動階次的增加,主軸各階振動加速度均呈周期性波動逐(zhú)漸減小(xiǎo),前(qián)期波動幅度較大,最後(hòu)直至趨於平穩。而(ér)在滾齒機低轉速切削時,主軸出現顫振現象,對齒(chǐ)輪加工精度與質量(liàng)具有較大影(yǐng)響,明滾(gǔn)齒機在低轉速加工初期振動響應影響極為顯著(zhe)。當ht =45 mm,5n =10 r/min 時,第 1 階最大加速度幅值約為 580.5 m·s2,第 3 階最大加速度幅值約為 1580.5 m·s,第 5 階(jiē)最大加速度幅值(zhí)約為 1604 m·s2。由此可見滾齒機加工中,高轉速滾削(xuē)齒輪比低轉速更為穩定.
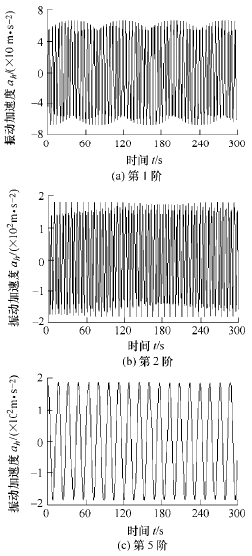
圖 8 滾刀主軸振動加速度-時間關係(xì)曲線
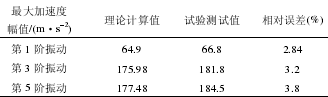
表 5 為滾刀主軸振動最大加速度幅值的理論模型計算與試驗測試對比
由主軸振動測試加速度值與滾(gǔn)齒切削(xuē)深度的(de)加速(sù)度-切削深(shēn)度關係曲線圖 10 可知,當滾齒機主軸轉速(sù)5n 為 40 r/min 且不變時(shí),滾刀主軸振動加(jiā)速(sù)度(dù)隨著滾切深度與(yǔ)振動階次(cì)增加而(ér)增大,主軸各(gè)階(jiē)振動加速度均(jun1)呈周期性波動(dòng)逐漸增(zēng)大,且波動幅度也(yě)較大。滾齒機采用大滾切深度切削時(shí),主(zhǔ)軸產(chǎn)生(shēng)顫振(zhèn)現象越嚴(yán)重,將對加工精度與質量造成較大影響,表明隨著滾切深度量的(de)增加主軸(zhóu)振動響應影響較為顯著。當ht =150 mm,5n =40 r/min 時,第 1 階的最大加速度幅值達到約 169.4 m·s2,第 3 階的最大加速度幅值達到約 468.7 m·s2,第 5 階的最大加速度幅值(zhí)達到約 478.9 m·s2。由此可見滾齒機加(jiā)工中,采用小滾(gǔn)切深度量與多刀(dāo)次(cì)滾削齒輪比大滾切深度量更為穩定。
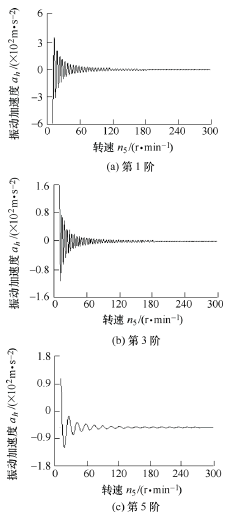
圖 9 滾刀主軸振動加速度-轉速關係曲線
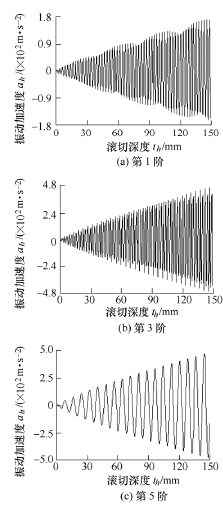
圖 10 滾刀主軸振(zhèn)動加速度-滾切深度關係曲線
3.3 滾刀主(zhǔ)軸振動位移響應分(fèn)析
由圖 11 有,當滾齒機滾切深度ht =45 mm,主軸轉速5n =40 r/min,且均不變時,滾刀主軸 X 方向振動位移隨滾齒時間均呈(chéng)等幅值周期性變化,滾刀主軸在 X 向呈現左右擺振現象;表明滾齒加工中滾刀(dāo)與工件摩擦切削齧合,對滾刀主軸振動響應是以周期性動態激勵為(wéi)主要影(yǐng)響,但該結構滾刀(dāo)主(zhǔ)軸動平衡效果較好。
由圖(tú) 11 可知,當ht =45 mm,5n =40 r/min 時(shí),滾刀主(zhǔ)軸第(dì) 1 階的最大位移幅值約為(wéi) 1.086×10-3 mm,第 3 階的最大位移幅值約為 3.6×105 mm,第5 階的最大位移幅值約為 4.8×106mm;當滾齒機主軸轉速5n 為 40 r/min,工(gōng)件滾切深度ht 為 45 mm 時。 由表 1 與圖 11 可得,滾刀主軸振動最大(dà)位移幅值的理論模型計算與測(cè)試對比數據(表 6);由表 6可知,理論與測(cè)試值間的相對誤差均小於 5%,即理論計算與(yǔ)測試值的一致(zhì)性較好,驗證(zhèng)了該型號滾齒機滾刀主軸振動位移(yí)響應理(lǐ)論推導模型的(de)正確性(xìng),該方法為其他係列(liè)滾齒機主軸振動特性理論與(yǔ)試驗研究提供經驗(yàn)借(jiè)鑒與參考作用。

圖 11 滾刀主軸振動(dòng)位移量(liàng)-時間關(guān)係曲線

表(biǎo) 6 為滾刀主軸振動的最大位移幅值理論模型計算與試驗測試對比
圖(tú) 12 為獲(huò)取的機床主軸振(zhèn)動位移與主軸轉速建立了振動位移-主軸轉速關係曲線(xiàn),當滾切深度ht為 45 mm 且(qiě)不變(biàn)時,在齒輪(lún)加工初期與低轉速工況下(xià),滾(gǔn)刀主軸振動位移量較大;且隨著轉速與振動階次(cì)的增加(jiā),主軸振動(dòng)位移量均呈周期性波動逐(zhú)漸減小,前期波動幅度較大,最(zuì)後逐漸趨於平(píng)穩且變(biàn)化量很小(xiǎo),表明該主軸(zhóu)係統(tǒng)幾何(hé)精度及動平衡控製較好。
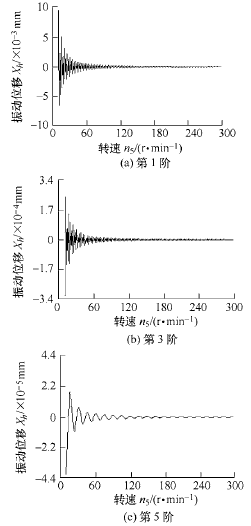
圖 12 滾刀主軸振動位移量(liàng)-轉速關係曲線
在(zài)滾齒機低轉速切削時,主軸出現顫振,振(zhèn)動位移相對較大,對齒輪加工精度與質量將會產生(shēng)直接影響,表明滾齒機在低轉速加(jiā)工初期振動(dòng)響應影響較為明顯。當ht =45 mm,5n =10 r/min 時,第1階的最大位移(yí)幅值約為 9.47×103 mm,第 3 階的最大位移幅值約為 3.18×104 mm,第 5 階的最大位(wèi)移幅值約為 4.2×105 mm。由(yóu)此可(kě)見(jiàn),滾齒機高轉速滾削加工齒輪(lún)比(bǐ)低轉速更為穩定。
圖 13 可知(同(tóng)理,整理出主軸振動位移量-切削深度關係曲線),當滾齒機主軸轉速5n 為 40 r/min且不變時,滾刀主軸振(zhèn)動位移量隨(suí)著滾切深度與(yǔ)振動階次的增加而增大,且波(bō)動幅度也較大。滾齒機
采用(yòng)大滾切深度切削(xuē)時,主軸顫振現象較為顯(xiǎn)著,對齒輪加工精度與質量(liàng)的影響大,表(biǎo)明隨著滾切深度量(liàng)的增加主軸(zhóu)振動響應影響較為明顯。當ht =150 mm,5n =40 r/min 時,第(dì) 1 階的最大位移幅值約 2.85×103 mm,第 3 階的最(zuì)大位移幅值約9.6×105 mm,第 5 階的最大位(wèi)移幅值約 1.2×105 mm,由此可(kě)見滾齒機齒輪(lún)加工(gōng)中,采用小滾(gǔn)切深度與多刀次滾削齒輪比大滾切深度更為穩定(dìng),且(qiě)振動位移量也較小,可降低或(huò)減小滾齒位置偏差。

圖 13 滾刀主軸(zhóu)振動位(wèi)移(yí)量-滾削深度關(guān)係曲線
由以上分析可知,滾刀主軸在滾齒機低轉速加工初期,將會產生較為嚴重振動(dòng)現象,但在滾削深度不(bú)變情(qíng)況下振(zhèn)動位移響應逐漸減小,直至趨於平穩。在轉速不變情況下,主軸振動位移隨著滾削深度的增長而呈波動性快速增加(jiā)。滾刀主軸在 X 方(fāng)向的左右擺振,使齒輪齒麵出現振紋。因此,滾(gǔn)齒加工中,盡(jìn)量采用大轉速(sù)、小滾切(qiē)量及多(duō)刀次切削加工齒輪,使機床主軸(zhóu)振(zhèn)動響應更為穩定,可降低或減少滾齒機振動,從而(ér)降低或減少對齒輪加(jiā)工精度與質量的影響。
4、結論
(1) 采(cǎi)用簡支梁與 Euler-Bemoulli 梁理論,推導出滾(gǔn)齒機滾刀主軸振動加速度與(yǔ)位移響應函數模型,並根據主軸結構與加工工藝參數(shù),可直接(jiē)計算(suàn)各振動(dòng)階次對應的振動加速(sù)度與位移數(shù)據。
(2) 通過對滾刀主軸振(zhèn)動最大加速度、位移幅(fú)值的理論模型計(jì)算(suàn)與測試數據比(bǐ)較分析可知,理(lǐ)論與測試值之間的相(xiàng)對誤差均小於 5%,表明理論與試(shì)驗值一致性較好(hǎo),驗證了該型號滾齒(chǐ)機(jī)滾刀主軸振動響應函數理論推導模型(xíng)的正確性。
(3) 由振動加速度(dù)、位移測試數據曲線可知,滾齒機(jī)滾刀主軸在 X 方向發生左(zuǒ)右擺振,使滾齒切削點產生相應振擺,將造成齒輪齒向、切向或螺(luó)旋線錐度誤差。
(4) 經對振動加速度、位移分別同主軸工作轉速(sù)、滾削深度的測(cè)試數據曲(qǔ)線分析(xī)可知(zhī),滾齒加工中盡量提高滾刀(dāo)主(zhǔ)軸轉速,降低切削力,采用小滾切深度(dù)與多刀次切削加工齒輪,會降低或減少滾(gǔn)齒機振動,從而可降低齒麵振紋,確保機床振(zhèn)動響應與加工穩定性,減小或降低機床由振動引起加(jiā)工(gōng)誤差(chà),提(tí)高齒輪加工精度(dù)與質量。
(5) 該研究工作為滾齒機工(gōng)件主軸振動特性,非接觸式傳感器應用,滾刀主軸與齒輪工件主軸間相對(duì)振動特性,以及機床故障診斷等方麵問題後期深入、實用(yòng)性的理論與試驗研究奠定了基礎。
投稿箱:
如果您有機床行業、企業相關(guān)新聞(wén)稿件發表,或進行(háng)資訊合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關(guān)新聞(wén)稿件發表,或進行(háng)資訊合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息(xī)
業(yè)界視點
| 更多
行業數據
| 更多
- 2024年11月 金屬切削機床產量數(shù)據
- 2024年11月 分地區金屬切削機床產量數據
- 2024年11月 軸承出口(kǒu)情況
- 2024年11月 基本型(xíng)乘用車(轎車)產量數據
- 2024年11月 新能源汽車產量數據(jù)
- 2024年11月 新能源汽車銷量情況
- 2024年10月 新能源汽車產量數據
- 2024年10月 軸承出口情況
- 2024年(nián)10月 分地區金屬切削機床產量數據
- 2024年10月 金屬切削機床產量數據(jù)
- 2024年9月 新能源汽車銷量情(qíng)況(kuàng)
- 2024年8月 新能源汽車產量數據
- 2028年8月 基本型乘用車(chē)(轎車)產量數據





